Определение усилий в колоннах рамы. Расчет трехпролетной рамы

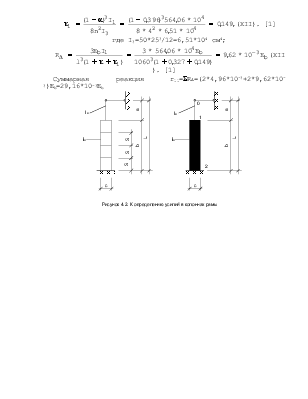
 4. Определение усилий в колоннах рамы.

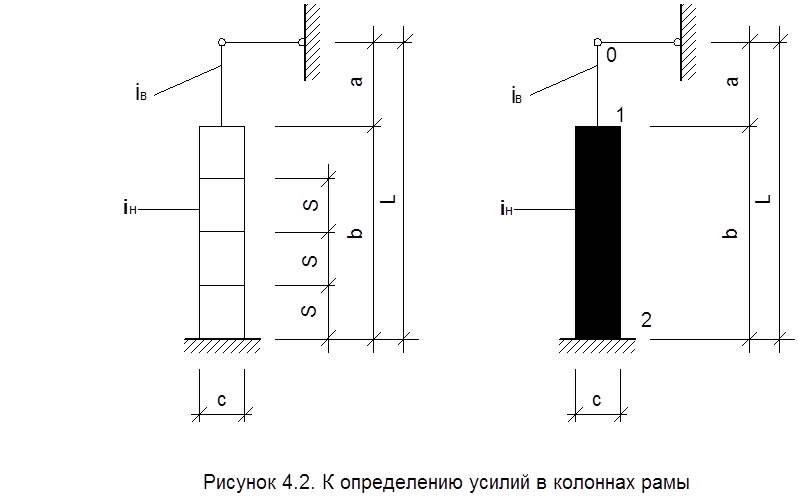
Расчет рамы выполняется методом перемещений. Неизвестным является D₁ – горизонтальное перемещение верха колонн. Основная система содержит горизонтальную связь препятствующую этому перемещению (рисунок 4.1).

Каноническое уравнение метода перемещений имеет вид:

С_dinr₁₁D₁₁+R_1p=0,

Где R_1p – реакция верха колонн от внешнего воздействия; С_din – коэффициент учитывающий пространственный характер работы каркаса.

Постоянная, снеговая, ветровая нагрузки действуют одновременно на все рамы температурного блока, при этом пространственный характер работы каркаса здания не проявляется, С_din = 1.

Крановая нагрузка приложена только к нескольким рамам блока, однако благодаря жесткому диску покрытия в работу вовлекаются все рамы температурного блока, проявляется пространственная работа,  С_din 1.

Подвергаем основную систему единичному перемещению D₁ = 1 (рисунок 4.1.) и вычисляем реакции верхнего конца сплошной и двухветвевой колонны R_D по формулам прил. (XII). [1]

D=1

                                                                                 

ВD

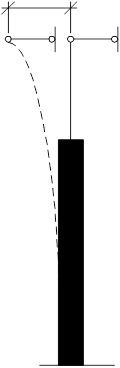Для сплошной крайней колонны:

a = а/l = 4,2/10,6 =0,396.

Где а = Н₂ =4,2 м, l = Н = 10,6 м;

k = a³(I₁/I₂ - 1) = 0,396³(213*10⁴/90*10⁴ - 1) = 0,08,

где I₁=(50*80³)/12=213*10⁴ см⁴; I₂=(50*60³)/12=90*10⁴ см⁴;k₁=0;

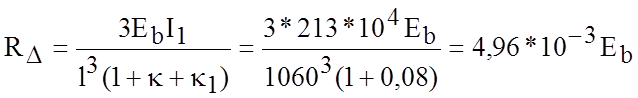.(XII). [1]

Рисунок 4.1.

Для средней двухветвевой колонны при числе

                панелей n =4;

a = а/l = 4,2/10,6 =0,396. (XII). [1]

Где а = Н₂ =4,2 м, l = Н = 10,6 м;

k = a³(I₁/I₂ - 1) = 0,396³(564,06*10⁴/90*10⁴ - 1) = 0,327, (XII). [1]

где I₁=2bh(c/2)²=2*50*25*25(95/2)²=564,06*10⁴ см⁴; I₂=(50*60³)/12=90*10⁴ см⁴;

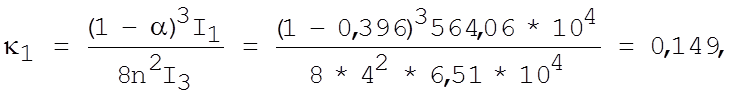(XII). [1]

где I₃=50*25³/12=6,51*10⁴ см⁴;

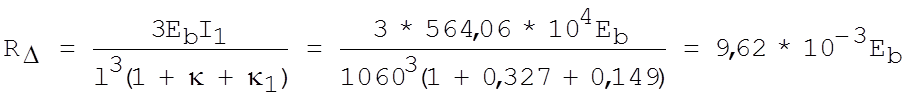(XII). [1]

Суммарная реакция r₁₁=SR_D=(2*4,96*10^-3+2*9,62*10^-3)Е_b=29,16*10^-3Е_b

Усилия в колоннах рамы от постоянной нагрузки:

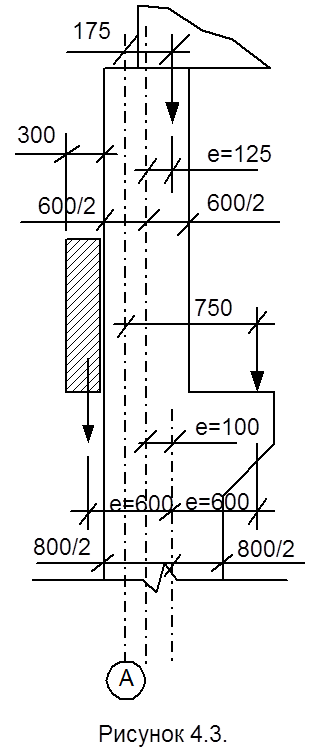Продольная сила F₁=408,83 кН на крайней колонне действует с эксцентриситетом е₀. (рисунок 4.3.).

В верхней части е₀ = 0,25+0,175-0,5h = 0,25+0,175-0,5*0,6 = 0,125 м, момент М₁=F₁*е₀ =408,83*0,125=51,1 кН*м, где 0,125 – привязка крайних колонн к разбивочным осям; 0,175 – расстояние от продольной разбивочной оси до передачи продольной силы на колонну.

В подкрановой части кроме силы F₁, приложенной с эксцентриситетом е₀=(h₁-h)/2 = (0,8-0,6)/2=0,1 м, действуют расчетная нагрузка от стеновых панелей толщиной 30 см F=200,13 кН, с е₀=0,3/2+0,8/2=0,55 м; расчетная нагрузка от подкрановых балок F = 120,2 кН, с е₀ = l+0,25-0,5h=0,75+0,25-0,5*0,8=0,6; расчетная нагрузка от надкрановой части колонны F=32,9 кН, с е₀ = 0,1 м.

Суммарное значение момента М₂ = -408,83*0,1-200,13*0,55+120,2*0,6-32,9*0,1=-82,12 кН*м.

Вычисляем реакцию верхнего конца левой колонны по формуле (приложение XII): [1] (рисунок 4.4)

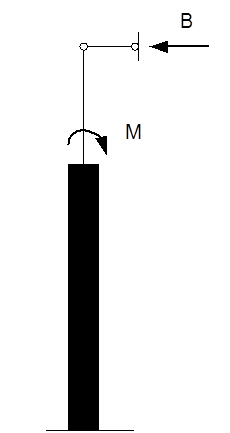
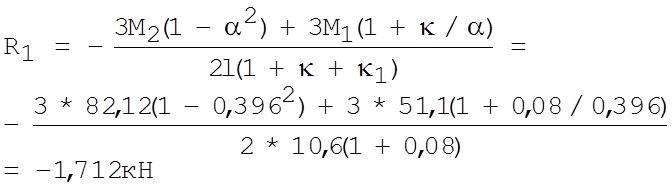
(Приложение .XII). [1]

Рисунок 4.4.

Согласно принятому в расчете правилу знаков, реакция, направленная вправо, положительна. Реакция правой колонны R₃= 1,712 кН, средней колонны R₂ = 0(так как загружена центрально). Суммарная реакция связей в основной системе R_1p = SR_i = -1,712+0+1,712=0, при этом из канонических уравнений r₁₁D+R_1p = 0  следует, что D₁=0.     Упругая реакция левой колонны R_е=R₁+D₁R_D=-1,712 кН.

Изгибающие моменты в сечениях колонны (рисунок 4.5 [а]) равны:

М_0-1=М₁=51,1 кН*м,

М₁₀=М₁+R_eH₂=51,1-1,712*4,2=43,91 кН*м; М₁₂=51,1-82,12=-31,02 кН*м; М₂₁=51,1-82,12-1,712*10,6=-49,16 кН*м.

Продольные силы в крайней колонне: N₁₀=408,83+32,9=441,73 кН; N₁₂=441,73+200,13+120,2=762,06 кН; N₂₁=762,06+66,88=828,94 кН;

Поперечная сила Q₂₁=1,712 кН;

Продольные силы в средней колонне: N₁₀=817,66+32,9=850,56 кН; N₁₂=850,56+2*120,2=1090,96 кН; N₂₁=1090,96+69,23=1160,19 кН.

Усилия в колоннах от крановой нагрузки.

Рассматриваются следующие виды загружения 1) М_max на крайней колонне М_min на средней колонне (рисунок 4.5, г); 2)  М_max на средней колонне М_min на крайней колонне(рисунок 4.5, д); 3) четыре крана с М_max на средней колонне; 4) тормозная сила на крайней колонне (рисунок 4.5, е); 5) тормозная сила на средней колонне (рисунок 4.5, ж).

Загружение М_max на крайней колонне М_min на средней колонне (рис 4.5, г).

На крайней колонне D_max = 867,36 кН приложена с эксцентриситетом е=0,6 м (аналогично эксцентриситету приложения нагрузки от веса подкрановой балки (рисунок 4.3.)

 Момент в узле М_max = 867,36*0,6=520,41 кН*м.  

Реакция верхней опоры левой колонны:

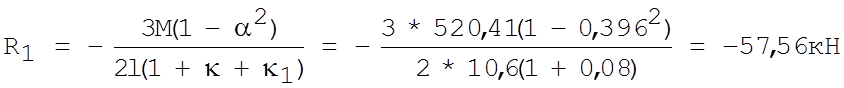
(Приложение .XII). [1]

Одновременно на средней    колонне действует сила D_min= 220,28 кН с эксцентриситетом е = l = 0,75. При этом М_min = 220,28*0,75=162,21 кН*м.

Реакция верхней опоры средней колонны:

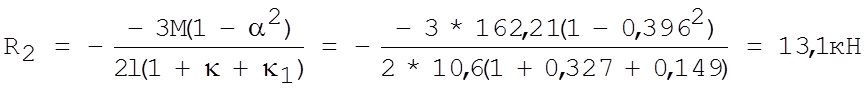
(Приложение .XII). [1]

Суммарная реакция в основной системе R_1p= - 57,56+13,1=- 44,46 кН;

С учетом пространственной работы:

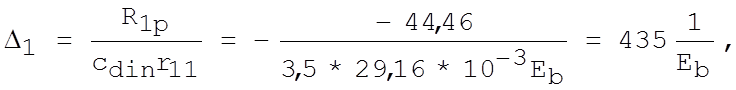(XIII.21) [1]

где с_din=3,5 при шаге колонн 12 м.

Упругая реакция левой колонны R_e=-57,56+4,96*10^-3Е_b 435*1/Е_b=-55,4 кН;

Изгибающие  моменты   в    расчетных сечениях левой колонны: М₁₀ = -55,4*4,2=-232,68 кН*м;