Свойства корреляции. Связь между зависимостью и коррелированностью. Условные распределения компонент

Независимость НДвСВ

 – независимы, если

Пример:

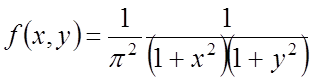 – двумерное распределение Коши.

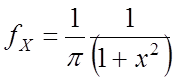
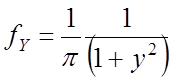
Ковариация (корреляционный момент)

 – размерная величина. Измеряемая в квадратах величин  или . Это очень не удобно  вводят безразмерную величину – корреляция (коэффициент корреляции)

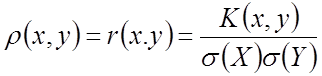
Свойства корреляции:

1.  Если  – независимы, то , однако выражение

 – независимы

не верно

2. 

3.  Коррелированные , если

Докажем:

Введем вспомогательную СВ

Посчитаем её дисперсию

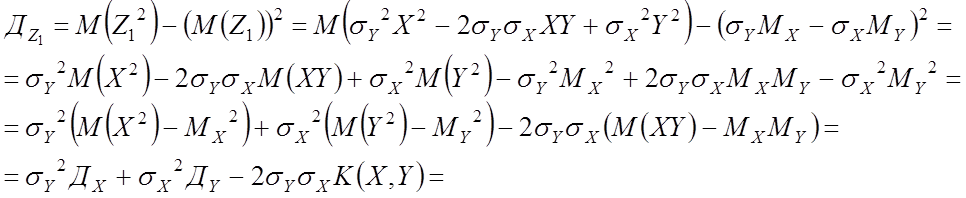
Для доказательства  вводят

Связь между зависимостью и коррелированностью.

Независимость влечет некоррелированность

Если  и  – независимы  необязательно, что и   –  независимые.

Пример:

  –  равномерно распределена на

  зависит от

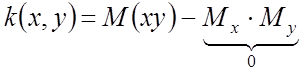
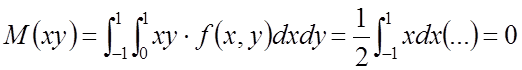
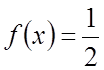
Если линейная зависимость

   

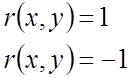
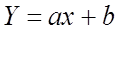
  –  для нормированных случайных величин.

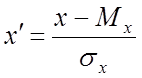  –  нормированная случайная величина (не значит производная)

 ,

   Критерий независимости..

 и  независимы   или

  –  нормирова

Зная плотность совместного распределения , можно найти интегральную функцию

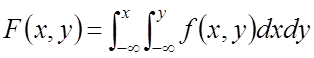 и обратно из  надо взять вторую производную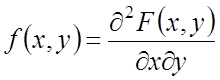

Условные распределения компонент.

Дискретный случайный вектор

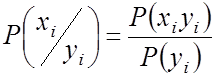
Условное распределение  при :

				…
				…

Непрерывный случайный вектор

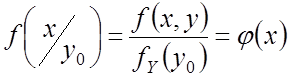
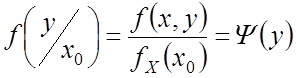
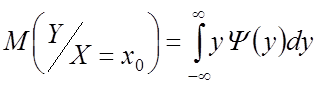 – математическое ожидание , или функция регрессии.

Двухмерная нормально распределенная случайная величина.

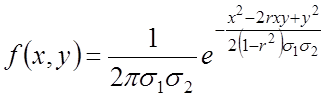
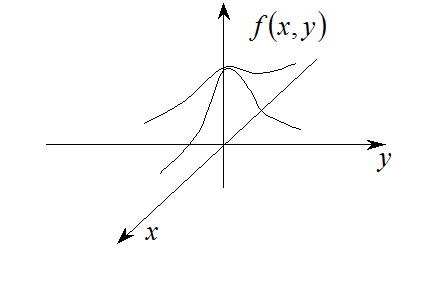
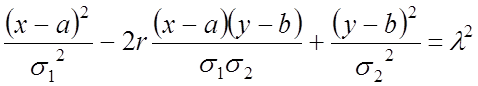 – эллипс равных вероятностей

2.8. Функция случайной величины

Одномерная случайная величина

 – СВ – функция случайной величины

Пример 1:

	0	1	2
	0,1	0,5	0,4

Если функция  задана в виде:

          , то

	– 1	1	3
	0,1	0,5	0,4

Пример 2:

	– 1	0	1
	0,1	0,2	0,7

Задавая , получим

	0	1
	0,1	0,8

Пусть , то есть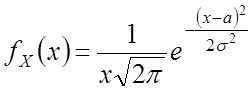

Если , то  – ?

Известно:

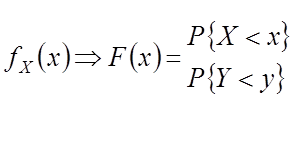
Если  монотонно возрастает

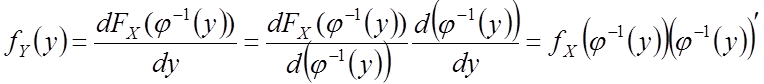
для монотонно убывающей функции плотность останется положительной, а производная  –  отрицательная

берут

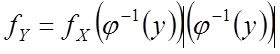 – формула распределения НСВ

Так как у нас , то

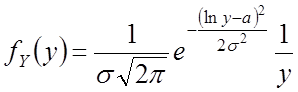 – плотность логнормального распределения

График

Пример:

 – очки на I кости

 – очки на II кости

	1	2	3	4	5	6			1	2	3	4	5	6

Тогда расперделение  будет

	1	2	3	4	5	6	7	8	9	10	11	12

Вывод: Если расперделение независимых величин равномерно, то распределение их суммы не равномерно.

 – справедливая игра

2.9. Композиция(сумма) случайной величины

ДСВ:

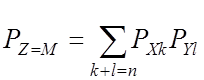
НСВ: ,  – плотности  и

           – независимы

 – фиксировано

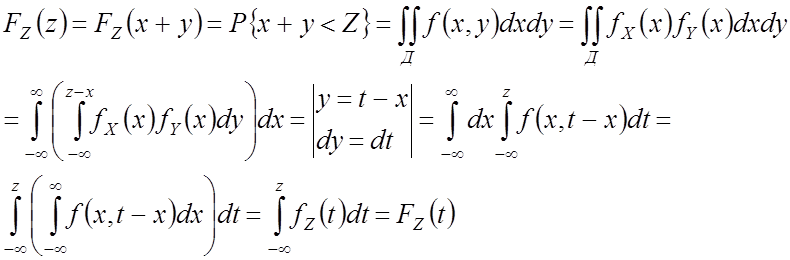
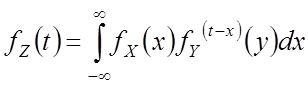
 – свертка

Если распределения суммы и распределения слагаемых одинаковы, то такие распределения называют устойчивыми. Например, нормальное распределение

     

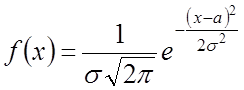
Пример:

Пусть  и  изменяются по закону экспоненты:

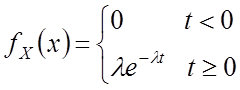
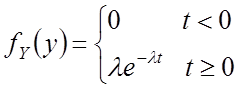
Найти

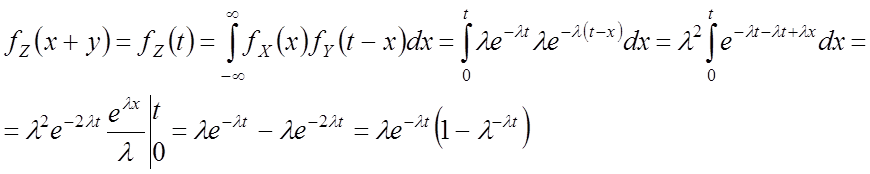
распределение Эрланга II порядка

Если ,  – нормированные нормальные СВ, тогда

 распределение "кси – квадрат"

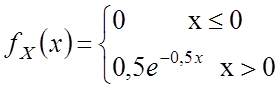
2.10. Закон больших чисел

1.  Неравенство Чебышева

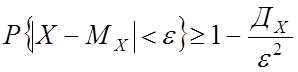
Доказательство:

 Для НСВ:

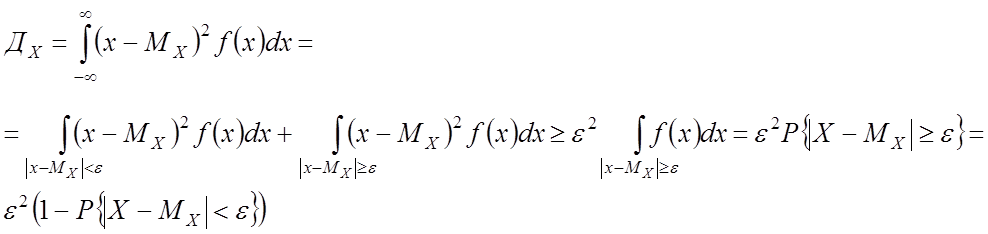
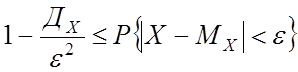
2.  Теорема Бернулли

Пусть в схеме Бернулли производят  независимых испытаний,  –  вероятность успеха в одном опыте,  вероятность неудачи,  – число успехов.

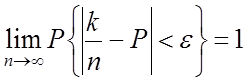
Доказательство производят на основании теоремы Чебышева:

,

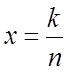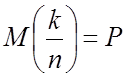
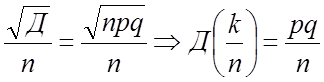
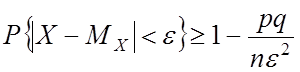
3.  Теорема Чебышева

Пусть  – попарно независимые СВ

Причем ,

 

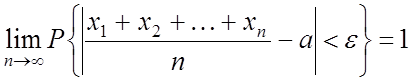
Доказательство:

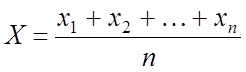
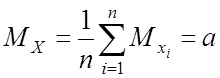
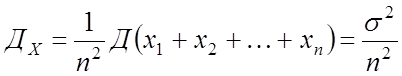
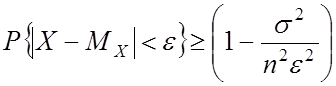
4.  Центральная предельная теорема Ляпунова

Пусть  – одинаково распределенные независимые СВ с одинаковыми математическими ожиданиями  и дисперсиями при достаточно больших  распределение суммы этих величин близко к нормальному с теми же параметрами.

3. Случайные процессы

3.1. Понятие случайных процессов

Случайный процесс(случайная функция или стохастический процесс) (СП)– случайная величина, зависящая от параметра (времени, например)

 – случайный процесс – функция, значение котрой в каждый момент времени есть случайная величина.

где  – элементарный исход

Примеры:

1)  Скорость движения по траектории

2)  Помехи радио приема

3)  Процессы миграции

4)  Процессы гибели и размножения

Способы изучения  СП:

1.   

Сечение СП  – случайная величина, получаемая при фиксированном времени .

2.   

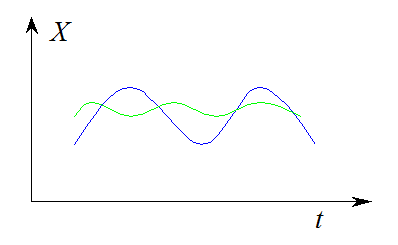
Фиксируют результат опыта

Траектория (реализация) СП – неслучайная функция от , получаемая в результате опыта

Классификация СП

	Непрерывное	Дискретное
Непрерывный	1.  Непрерывный СП в непрерывном времени	2.  Непрерывный СП в дискретном времени
Дискретный	3.  Дискретный СП в непрерывном времени	4.  Дискретный СП в дискретном времени

Примеры:

1.   – напряжение в сети

2.  вес ребенка

3.  число заявок на АТС

4.  число студентов на курсе

Примеры элементарных СП:

1) 

равномерно распределена на

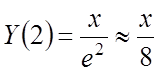
Если , то

2) 

,

3) 

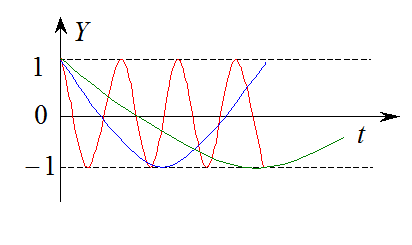
4) 

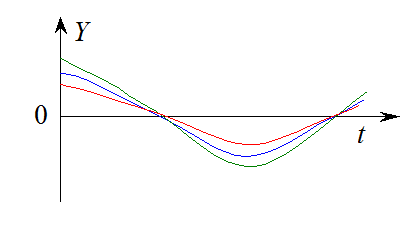
3.2. Распределение СП и его характеристики

,  – фиксировано