![]() –
функция распределения
–
функция распределения
Одномерный закон распределения СП
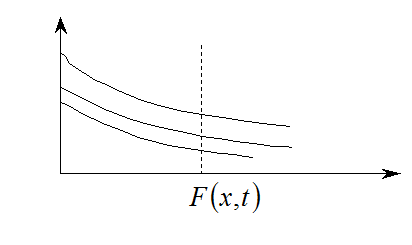
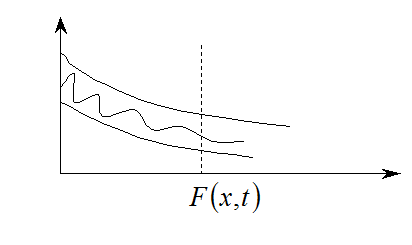
![]() одинаковы
для данного
одинаковы
для данного ![]()
Двумерный закон распределения СП
![]()
![]() ,
, ![]() – переменные
– переменные
Характеристики СП
1. Математическое ожидание
![]() –
неслучайная функция, которая в каждый момент времени
–
неслучайная функция, которая в каждый момент времени ![]() принимает
значение математического ожидания соответствующего сечения.
принимает
значение математического ожидания соответствующего сечения.
дискретное 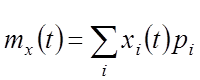
непрерывное 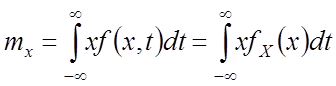
2. Дисперсия
![]() –
неслучайная величина, которая в каждый момент времени принимает значение
дисперсии соответствующего сечения
–
неслучайная величина, которая в каждый момент времени принимает значение
дисперсии соответствующего сечения
![]()
3. Корреляционная функция
![]() – корреляционный
момент между двумя сечениями СП
– корреляционный
момент между двумя сечениями СП
![]() называют
ещё автокорреляционной функцией
называют
ещё автокорреляционной функцией
Свойства корреляционной функции
1.
![]()
2.
![]()
3.
![]()
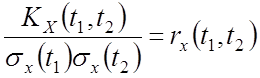 – нормированная
корреляционная функция
– нормированная
корреляционная функция
Пример:
![]()
![]()
![]() ,
, ![]() – не зависят от
– не зависят от ![]()
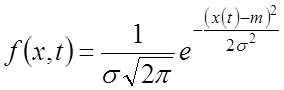
![]() ,
, ![]() – ?
– ?
![]()
![]()
![]()
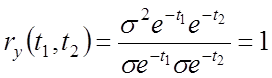 –
нормированная корреляционная функция экспоненты с нормальным распределением.
–
нормированная корреляционная функция экспоненты с нормальным распределением.
![]() –
корреляционная функция
–
корреляционная функция
![]() –
взаимная корреляционная функция СП
–
взаимная корреляционная функция СП ![]() и
и ![]()
![]()
![]()
Дифференцирование СП
Производная СП – тоже СП
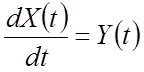
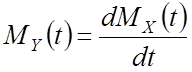 –
математическое ожидание
–
математическое ожидание
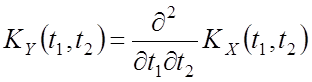 –
корреляционная функция
–
корреляционная функция
при ![]()
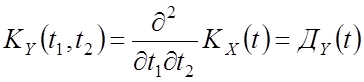
Интегрирование СП
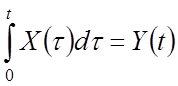
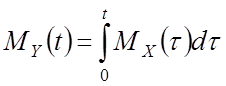 –
математическое ожидание
–
математическое ожидание
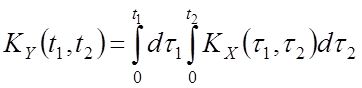
Характеристики суммы СП
Пусть ![]() –
СП и
–
СП и ![]() , тогда
, тогда
![]()
![]()
Доказательство:
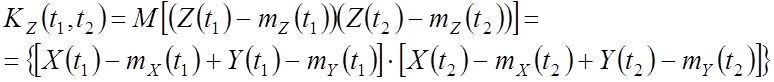
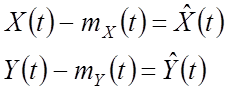 –
центрированные величины
–
центрированные величины
Тогда
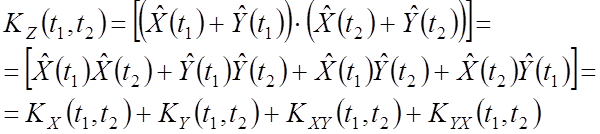
Если СП ![]() и
и ![]() не
коррелированны, то для любых сечений их взаимная корреляция будет равна 0, то
есть
не
коррелированны, то для любых сечений их взаимная корреляция будет равна 0, то
есть
![]()
а при ![]()
![]()
3.3. Разложение СП
Если ![]() ,
то
,
то ![]() – элементарная функция
– элементарная функция
Каноническое разложение СП
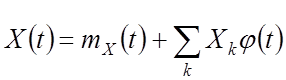 , где
, где
![]() –
математическое ожидание СП,
–
математическое ожидание СП,
![]() –
центрированные взаимно некоррелированные случайные величины – коэффициенты
случайного процесса, то есть
–
центрированные взаимно некоррелированные случайные величины – коэффициенты
случайного процесса, то есть
![]() ,
, ![]() при
при ![]()
если ![]() ,
то
,
то ![]()
![]() –
координатные функции они не случайны
–
координатные функции они не случайны
Любой случайный процесс имеет каноническое разложение
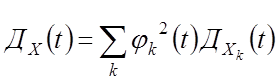
Существует множество способов
приведения СП к каноническому виду и конкретный способ зависит от статических
данных: ![]()
3.4. Стационарные СП (ССП)
ССП – СП, характеристики которого (математическое ожидание, дисперсия) не зависят от времени, а корреляционная функция зависит только от разности времен (промежутка времени)
Если СП – стационарный, то
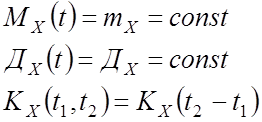
Пример:
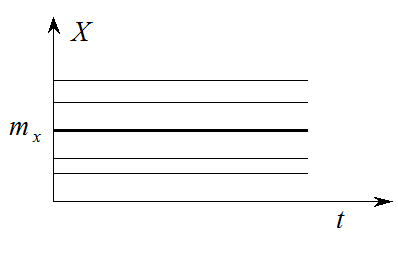
![]() –
четная
–
четная
![]()
Эргодичность ССП
Свойство эргодичности:
Любая реализация достаточно большой продолжительности является "полномочным представителем" любой другой реализации.
Если
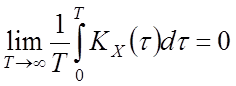 , то имеет место эргодический ССП
, то имеет место эргодический ССП ![]()
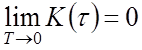
Каноническое разложение ССП
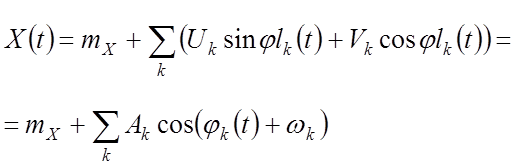
![]() – случайные амплитуды
– случайные амплитуды
![]() – случайные фазы
– случайные фазы
Пример ССП:
Случайная телеграфная волна
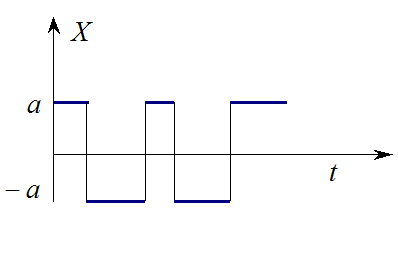
Имеем
простейший поток событий с интенсивностью ![]() .
.
Одномерная функция распределение примера:
|
|
|
|
|
|
0,5 |
0,5 |
![]() ,
, ![]()
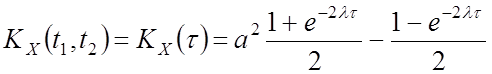
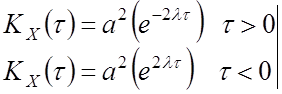
![]()
![]()
![]() это эргодичный ССП
это эргодичный ССП
3.5. Марковские процессы(МП)
Марковские
процессы – это случайные процессы, которые имеют дискретные состояния.
Обозначают: ![]()
![]() – множество состояний СП может быть очень
большим, но обязательно счетным.
– множество состояний СП может быть очень
большим, но обязательно счетным.
Теория графов
Пример ориентированного графа состояний
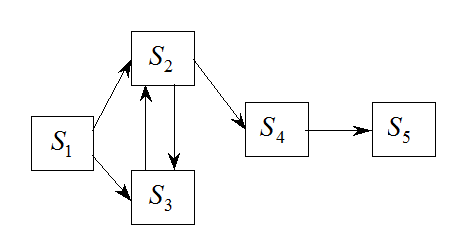
![]() –
вершина графа
–
вершина графа
![]() – ребра
графа
– ребра
графа
Источник – вершина, в которую не идет ни одна стрелка.
Например, ![]() .
.
Поглотитель – вершина, из которой не выходят ни одного ребра. В
данной примере это вершина ![]() .
.
Транзитивное состояние – вершина, в которую входят и выходят стрелки.
Связное множество состояний, или эргодическое – граф для которого можно из любого состояния (вершины) можно перейти в любое.
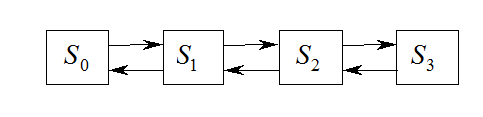
Процесс гибели или (и) размножения (отказа – восстановления)
![]() – вероятность
того, что СП принял значение
– вероятность
того, что СП принял значение ![]() в момент времени
в момент времени ![]() .
.
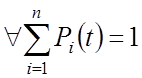 –
условие нормировки.
–
условие нормировки.
Установившийся режим
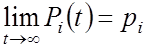
Если предельные вероятности состояний существует, то СП имеет стационарный (установившийся) режим.
Марковский
процесс – случайный процесс, у которого для любого момента ![]() вероятности состояний
вероятности состояний ![]() зависят только от вероятности состояний
зависят только от вероятности состояний ![]() при
при ![]() и не
зависят от (прошлого)
и не
зависят от (прошлого) ![]() при
при ![]()
Марковский процесс – случайный процесс, для которого вероятности состояний зависят только от настоящего и не зависят от прошлого.
МП с дискретным временем
(Цепи Маркова) (ЦМ)
![]()
![]()
![]()
Основная задача исследования ЦМ – это нахождение вероятностей на "к" – том шаге
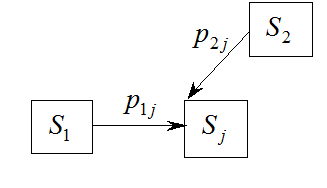
![]() – вероятность перехода из первого состояния
в "j" – тое
– вероятность перехода из первого состояния
в "j" – тое
![]() – вероятность перехода из
– вероятность перехода из ![]() в
в ![]() на
"к" – том шаге, Представляется собой матрицу перехода. На каждом шаге
эта вероятность в общем случае будет разной.
на
"к" – том шаге, Представляется собой матрицу перехода. На каждом шаге
эта вероятность в общем случае будет разной.
По формуле полной вероятности имеем
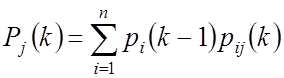
![]()
![]()
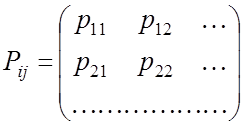
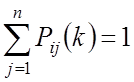 – условие нормировки
– условие нормировки ![]() матрицы перехода – стохастические матрицы,
так как для них выполняется условие нормировки.
матрицы перехода – стохастические матрицы,
так как для них выполняется условие нормировки.
ЦМ
однородна , если вероятности переходов не зависят от шага, то есть![]()
Пример:
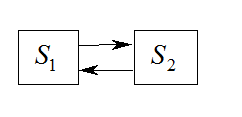
 – всегда дано
– всегда дано
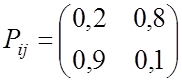
Найдем:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]()
![]()
Стационарный режим ЦМ
Существует, если:
1. Множество состояний эргодическое
2. ЦМ не однородна
3. ЦМ не должна быть цикличной
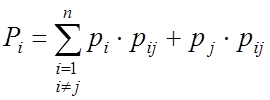
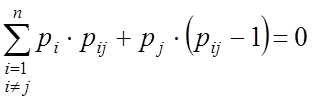
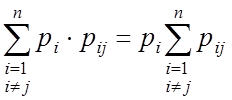 – балансовое уравнение для стационарного
режима ЦМ
– балансовое уравнение для стационарного
режима ЦМ
Суммарный поток, который входит в состояние равен суммарному потоку, который выходит из потока.
МП с дискретным состоянием и непрерывным временем
Пусть
переход из состояния "i" в "j" происходит под
воздействием пуассоновского потока событий с интенсивностью ![]()
![]()
Условие
![]() означает, что система остается на месте.
означает, что система остается на месте.
Если все потоки событий, переводящие систему из состояния в состояние пуассоновские и независимые, то такой СП называют Марковским.
Пусть
система имеет ![]() состояний
состояний
![]() ,
, ![]()
![]()
![]()
![]() – система осталась в состоянии "i"
– система осталась в состоянии "i"
![]() – система перешла в "i"
из каких-то других состояний.
– система перешла в "i"
из каких-то других состояний.
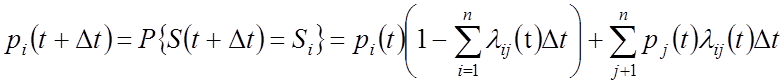
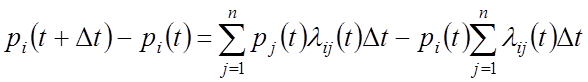
Делим
на ![]()
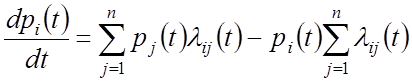 – уравнение Колмогорова для МП
– уравнение Колмогорова для МП
Однородный МП – это МП, для которого вероятности перехода из состояния в состояние не зависят от того, в какой момент времени система находилась в исходном состоянии, а зависит только от промежутка времени.
Если
![]()
Не зависит от времени стационарный пуассоновский поток.
Перепишем уравнение Колмогорова для однородного МП
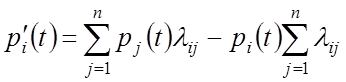
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.