Расчет системы передачи дискретных сообщений, страница 5

Рассчитаем вероятность неправильного приема кодовой комбинации длиной  n_кк=7 единичных элементов (код МТК-5 или ASCII) в предположении, что помехоустойчивое кодирование не используется, т.е. кратность исправляемой ошибки t_и = 0. Так как символы текста передаются кодовыми комбинациями, то вероятность искажения хотя бы одного единичного элемента кодовой комбинации будет определять вероятность неправильного дешифрирования (приема) символа.

Вероятность неправильного приема символов текста (комбинации) рассчитывается по формуле (8) стр. 14 Л1, где n_инф=n_кк=7. Величину  берем из п. 1.3.

,

0,01

Рассчитаем скорость передачи информации. Поскольку в каждой комбинации есть один проверочный разряд проверки на четность (код с проверкой на четность), то скорость передачи будет равна:

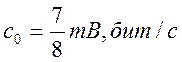
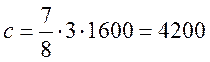  [бит/с]

Расчет вероятности неправильного приема символов и скорости передачи информации при использовании помехоустойчивого кодирования.

Определим, как будет изменяться вероятность неправильного приема символов текста, если использовать помехоустойчивые циклические коды, исправляющие, соответственно, одно, двух и трехкратные ошибки. Определим, как будет при этом изменяться скорость передачи информации с увеличением верности передачи символов за счет использования более помехоустойчивых кодов. Результаты расчетов изобразим в виде двух графиков:

 и 

Кратностью ошибки t_ош в принятой комбинации заданной длины n_кк называют количество искаженных элементов.

t_и=1; 2; 3.

Вероятность неправильного декодирования кодовой комбинации при исправлении ошибок будет определяться выражением:

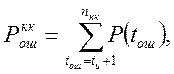
здесь

где 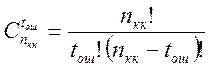  - число сочетаний из n_кк по t_ош.

Выполним расчеты для заданных кратностей исправляемых ошибок – t_и=1; 2; 3.

Сначала определим вероятности возникновения кратностей ошибок равных кратности исправления, т.е. t_ош=1, 2, 3.

1)  t_и=1

    

Требуемое количество проверочных символов выбираем из условия

    r=4, тогда 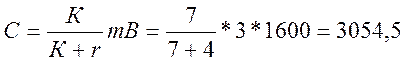    бит/с

n=к+r=7+4=11, т.е. имеем код (n,к)=(11,7)

Требуемое кодовое расстояние должно быть равно d_min=2t_и+1=2+1=3

2)  t_и=2

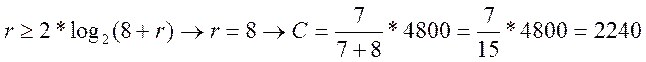 бит/с

тогда n=к+r=7+8=15,  тогда код (n,к)=(15,7)

d_min=2t_и+1=2*2+1=5

3)  t_и=3

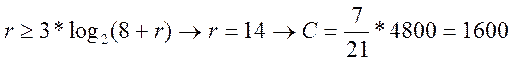 бит/с,

тогда имеем код (n,к)=(21,7)

d_min=2t_и+1=2*3+1=7

Так как помехоустойчивый код позволяет исправлять ошибки с кратностью до t_и включительно, то вероятность появления на выходе  декодера кодовых комбинаций с неисправленными ошибками будет равна сумме вероятностей ошибок с кратностью t_ош > t_и, т.е.

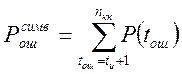
Тогда получим следующие результаты для каждого из t_и:

t_и=1

t_и=2

t_и=3

Для нахождения  нужно найти   Р(t_ош=4), она будет равна

Следовательно

Для построения заданных графиков  и   вначале сведем эти зависимости в таблицу 4.

Таблица 4.

tи	0	1	2	3
		4*10-5	7,2 * 10-8	1,75 * 10-10
С, бит/с	4200	3054	2240	1600

На рисунках 2 и 3 представлены графики полученных выше зависимостей и С от t_и.

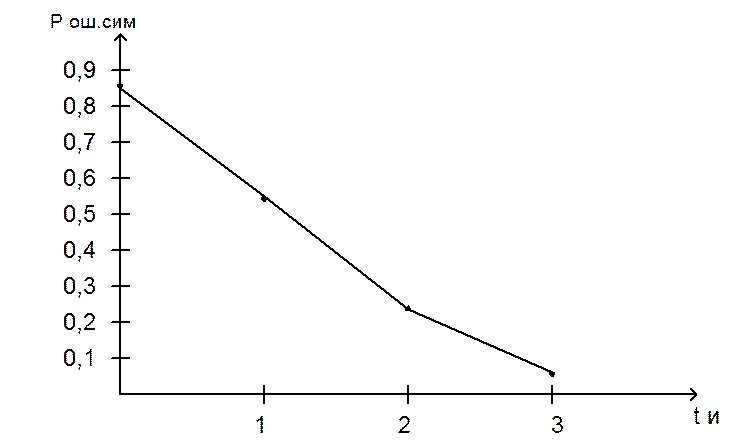
Рис.2. График зависимости Р _. =f(t_и)

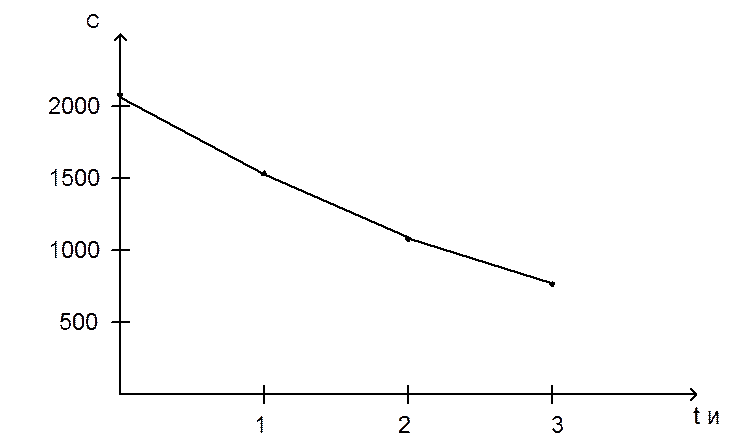
Рис.3. График зависимости С=φ(t_и)

Нахождение образующего полинома Р(х) циклического кода

Расчет Р(х)  выполняем в соответствии с методическими указаниями к выполнению курсового проекта и с использованием таблицы 2 минимальных многочленов для различных отношений r/t_и.

t_и=1:      r(t_и=1)=4; r/t_и=4:1=4

Это отношение определяет столбец, из которого нужно выбрать минимальные многочлены для индекса i=d_min-2. Так как для t_и=1 d_min=3, то i=3-2=1. Тогда Р(х) =х⁴+х+1

t_и=2:    r(t_и=2)=8;  r/t_и=8:2=4