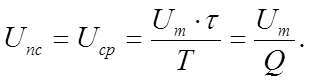 |
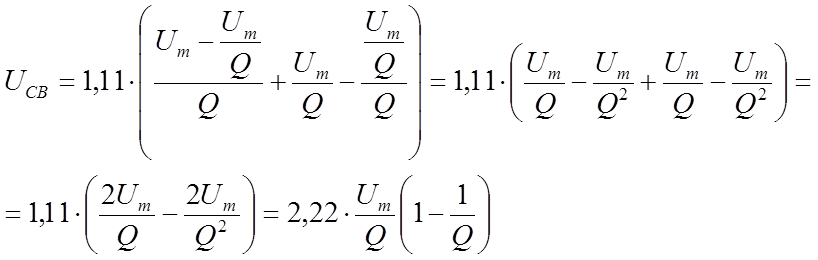 |
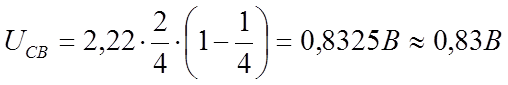 |
- 3) Показания вольтметра среднеквадратических значений (СК) с открытым входом , проградуированного в среднеквадратических значениях синусоидального напряжения , согласно 5.11 [1] не зависят от формы входного напряжения , следовательно :
UСК = U = 1 B
4. Указанные в задаче вольтметры имеют только аддитивную составляющую погрешность ΔUпр . Величину этой погрешности определяем из формулы 2.20 [2] :
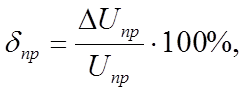 |
где Uпр - предельное значение шкалы прибора.
Отсюда : ΔUпр = δпр·Uпр/100 = 1,0 · 3/100 = 0,03 B
Находим относительные погрешности для результатов измерений
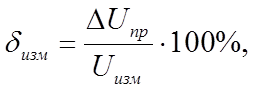 |
-
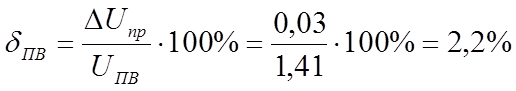 |
-
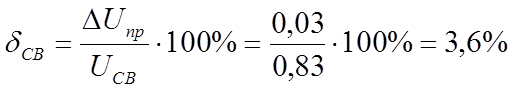 |
-
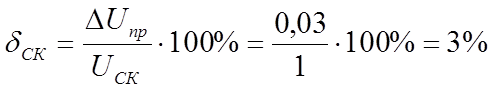 |
Задача № 1.4.
В формулах А, В, k и р - коэффициенты пропорциональности,
w = 2πf - круговая частота, где f - циклическая частота, связанная с образцовой частотой соотношением fг.обр = k·f , ψ и φ - начальные фазовые углы образцового и исследуемого напряжений. Требуется следующее :
1. Рассчитать по заданным значениям коэффициентов k и р частоту напряжения исследуемого генератора.
2. Графически построить фигуру Лиссажу, получающуюся на экране осциллографа при заданных значениях коэффициентов А, В, k , р , ψ и φ .
3. Считая образцовую частоту стабильной, определить абсолютную Δfиссл и относительную δfиссл нестабильность частоты исследуемого генератора для случая медленно изменяющейся фигуры Лиссажу, если за время, равное Т секунд, она повторно воспроизводится на экране не чаще N раз.
Исходные данные для решения :
|
m |
A |
B |
fг.обр , Гц |
φ , рад |
N |
|
0 |
3 |
1 |
100 |
π/2 |
5 |
|
n |
k |
p |
T , c |
ψ, рад |
|
1 |
1 |
1 |
10 |
π/2 |
Решение:
1.
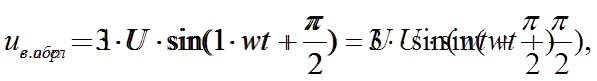 |
Очевидно, что частота напряжения исследуемого генератора равна частоте образцового генератора :
fиссл = fг.обр= 100 Гц
2.
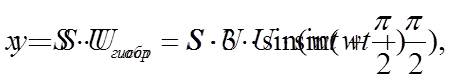 |
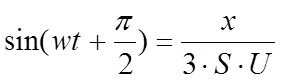 |
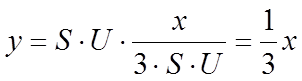 |
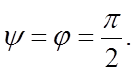 Полученное выражение является уравнением прямой,
проходящей через начало координат, лежащей в 1-ом и 3-ем квадрантах и
наклоненной под углом α = arctg(1/3). Для построения данной прямой достаточно знать две
точки . При построении учитываем, что частоты генераторов равны и начальная
фаза (при t=
0) одинакова
Полученное выражение является уравнением прямой,
проходящей через начало координат, лежащей в 1-ом и 3-ем квадрантах и
наклоненной под углом α = arctg(1/3). Для построения данной прямой достаточно знать две
точки . При построении учитываем, что частоты генераторов равны и начальная
фаза (при t=
0) одинакова
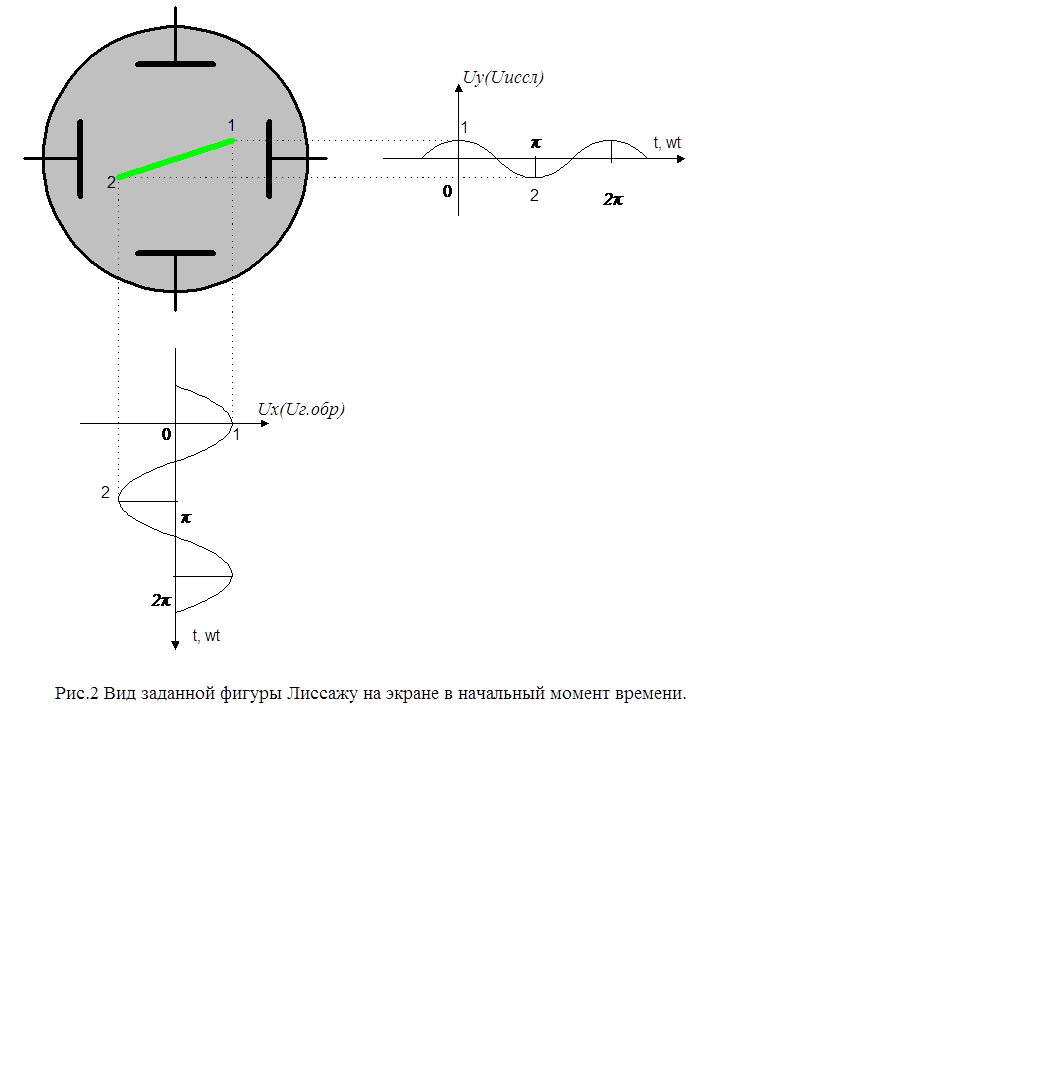
Графическое изображение фигуры Лиссажу представлено на рисунке 2.
3. В результате нестабильности частоты исследуемого генератора фигура на экране будет изменяться, принимая последовательно очертания эллипса, круга и прямой, перпендикулярной к начальной. Полностью фигура повторяется при отставании или опережении фазы на один период. Если бы фигура обладала полной симметрией, то она могла бы повторяться при отставании или опережении фазы на половину периода. Следовательно, абсолютную нестабильность частоты исследуемого генератора находим по формуле :
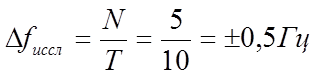 |
Находим относительную нестабильность частоты исследуемого генератора по формуле 2.2 [2] :
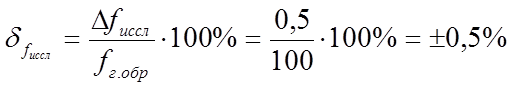 |
Задача № 2.1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.