Определение среднего арифметического значения для заданного числа измерений рабочего затухания. Определение среднего квадратического отклонения погрешности измерения. Определение максимальной погрешности, принятой для нормального закона распределения

Государственный комитет РФ по связи и информатизации

Сибирский государственный университет телекоммуникаций и информатики

МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ

И ИЗМЕРЕНИЯ В ТЕХНИКЕ СВЯЗИ

КОНТРОЛЬНАЯ РАБОТА № 1

Студент : Шерашов Михаил Валентинович

Группа : ЗМ-51

№ студ. билета : 951М-301

г. Новосибирск

1999

Вариант № 01.

        Задача № 1.1

    На междугородной телефонной станции производилась поверка измерителя рабочего затухания тракта транзитных соединений . С целью уменьшения влияния случайных погрешностей на результаты поверки , рабочее затухание Ар измерялось многократно в одних и тех же условиях . При этом было проведено n равноточных измерений арi . Считая , что случайные погрешности измерения распределяются по нормальному закону , определить :

1.  Среднее арифметическое значение Āр для заданного числа n измерений рабочего затухания .

2.  Среднее квадратическое отклонение     погрешности измерения .

3. 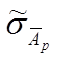 Максимальную погрешность ΔМ , принятую для нормального закона распределения .

4.  Среднее квадратическое отклонение           результата измерения (среднего арифметического значения).

5.  Границы доверительного интервала результата измерения рабочего затухания тракта для заданной доверительной вероятности Рдов .

6.  Систематическую составляющую погрешности измерения Δс , имеющейся на МТС измерительной установки , если в результате последующего измерения рабочего затухания приборами более высокого класса точности было установлено, что действительное значение рабочего затухания тракта транзитных сообщений составляет Ард децибел .

7.  Доверительную вероятность Рс.дов , с которой можно оценить найденное значение систематической составляющей погрешности .

Заданные значения (согласно номеру варианта) :

m	0
i	1-9
Рдов	0,88
n	1
i	34-39
Ард	16,94

i	1	2	3	4	5	6	7	8	9
аpi,дБ	16,24	16,19	16,25	16,41	16,36	16,52	16,64	16,81	16,93

i	34	35	36	37	38	39
аpi,дБ	16,97	17,12	17,23	17,34	17,10	17,23

    Решение :

Составляем таблицу по форме 1.4 "Методических указаний".

№ п/п	№ измерений  i	Значения аpi,дБ	аpi - Āр,дБ	(аpi - Āр)²,дБ²
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	1 2 3 4 5 6 7 8 9 34 35 36 37 38 39	16,24 16,19 16,25 16,41 16,36 16,52 16,64 16,81 16,93 16,97 17,12 17,23 17,34 17,10 17,29	-0,52 -0,57 -0,51 -0,35 -0,4 -0,24 -0,12 0,05 0,17 0,21 0,36 0,47 0,58 0,34 0,53	0,2704 0,3249 0,2601 0,1225 0,1600 0,0576 0,0144 0,0025 0,0289 0,0441 0,1296 0,2209 0,3364 0,1156 0,2809
15		∑ = 251,40	- 2,71   ∑ = 0 +2,71	∑ = 2,3688

1. 

Для нахождения Āр вычисляем сумму значений результатов всех (n = 15) единичных измерений :

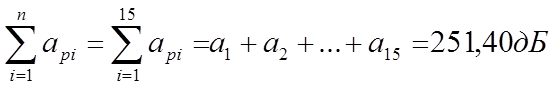Находим Āр по формуле 2.10 [2] :

 

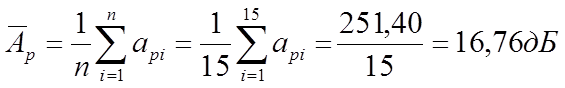Записываем результат : Āр =16,76 дБ .

Вычисляем значения аpi - Āр и (аpi - Āр)² , результаты заносим в таблицу .

2.  Находим среднее квадратическое отклонение         погрешности измерения по формуле 2.13 [2] :

Записываем результат :    = ± 0,41 дБ

3.  Принимаем максимальную погрешность измерения ΔМ = 3     (стр.43 [2]) :

ΔМ = 3·(± 0,41134) = ± 1,23402 дБ

Записываем результат : ΔМ = ± 1,23 дБ

4. 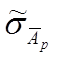 Находим среднее квадратическое отклонение           результата измерения по формуле 2.14 [2] :

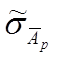Записываем результат :        = ± 0,11 дБ

5. 

Для заданной доверительной вероятности Рдов = 0,88 при числе измерений n = 15 по таблице 1.5 "Методических указаний" находим коэффициент распределения Стьюдента :

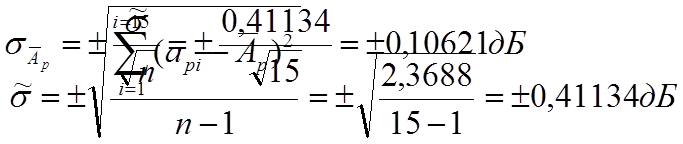                     tn = 1,656

     Пользуясь найденным значением , вычисляем доверительную

     погрешность результата измерения по формуле стр. 21

     "Методических указаний" :