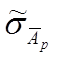Определение среднего арифметического значения для заданного числа измерений рабочего затухания. Определение среднего квадратического отклонения погрешности измерения. Определение максимальной погрешности, принятой для нормального закона распределения, страница 2

                     λ = Δдов = tn ·        = 1,656 · 0,10621 = 0,17588 дБ

Записываем результат : рабочее затухание тракта составляет

 Ар = 16,76± 0,18 дБ с доверительной вероятностью Рдов = 0,88

6.  Оцениваем величину систематической погрешности как разность между полученным результатом (средним арифметическим) и действительным значением затухания (измеренным прибором более высокого класса точности) Ард =16,94 дБ :

                     Δс = Āр - Ард = - 0,18 дБ

     Найденное значение выходит за рамки доверительного интервала

                    │- 0,18 │>│0,17588│⇒│ Δс │>│ Δдов │,

     следовательно , можно утверждать , что систематическая

     погрешность имеется .

7. 

Для вычисления доверительной вероятности систематической погрешности находим коэффициент Стьюдента по формуле на стр. 21 "Методических указаний" :

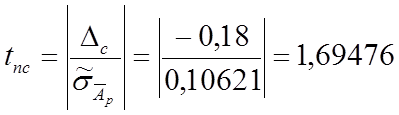По известным значениям коэффициента Стьюдента и числа измерений , по приведенной в приложении к "Методическим указаниям" программе (табл. П.2.2.) рассчитываем доверительную вероятность систематической погрешности :

Исходные данные : t = 1,695 ; n =15 .

Результат вычислений : Рn = 0,8853041 .

Записываем результат : Рс.дов = 0,8853

      Задача № 1.3.

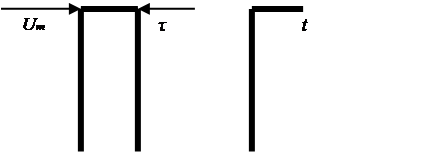
    На выходе исследуемого устройства имеет место периодическое напряжение , форма которого показана на рис. 1 . Это напряжение измерялось пиковым вольтметром (ПВ) , а также вольтметрами средневыпрямленного (СВ) и среднеквадратического (СК) значений, проградуированных в среднеквадратических значениях синусоидального напряжения . Каждый из вольтметров имеет как открытый , так и закрытый вход . Требуется определить :

1.  Среднее Uср , средневыпрямленное Uср.ви среднеквадратическое U значения выходного напряжения заданной формы .

2.  Коэффициенты амплитуды Ка и формы Кф выходного напряжения .

3.  Напряжения , которые должны показать каждый из трех указанных вольтметров с открытым (ОТКР) или закрытым (ЗАКР) входом . Характер входа определяется индивидуальным заданием .

4.  Оценить относительную погрешность измерения всех вычисленных согласно п. 3 напряжений , если используемые измерительные приборы имеют класс точности δпр и предельные значения шкалы Uпр , указанные в табл. 1.8 и 1.9.

Решение :

    Определяем индивидуальное задание для m =0 ; n = 1 :

-  Рисунок – 1.2.а ;

-  Период – Т = 80 мкс ;

-  Длительность импульса – τ = 20 мкс ;

-  Вход ПВ – ОТКР ;

-  Класс точности приборов – δпр = 1,0 % ;

-  Предельное значение шкалы приборов – Uпр = 3 В ;

-  Амплитуда напряжения – Um = 2 В ;

-  Вход СВ – ЗАКР ;

-  Вход СК – ОТКР .

1. 

Записываем общие выражения для среднего Uср , средневыпрямленного Uср.ви среднеквадратического U значений выходного напряжения в соответствии с формулами 5.2 , 5.3 и 5.4 [1] :

В приведенные формулы подставляем выражение U(t) . Для заданной формы сигнала напряжение U(t) описывается следующим образом :

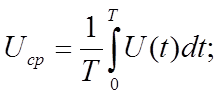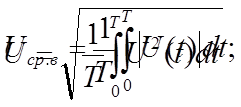              Um      при    0 ≤ t ≤ τ ,

U(t) =

               0        при    τ ≤ t ≤ T .

Подставляя данное выражение и интегрируя по участкам , находим :

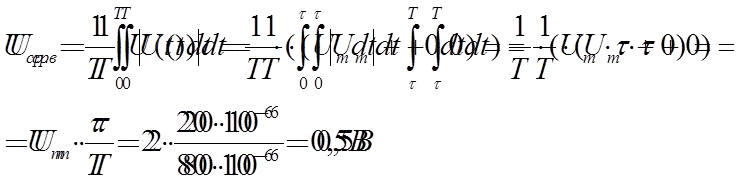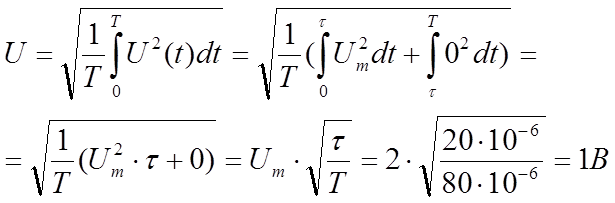2. 

Находим коэффициенты амплитуды Ка , формы Кф и усреднения Ку по формулам 5.5 ,5.6 и 5.7 [1] :

Неравенство    1 ≤ Кф ≤ Ка ≤ Ку выполняется .

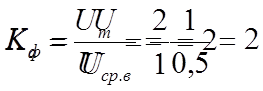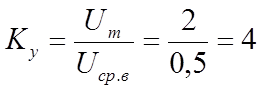3.  Находим напряжения , которые должны показать каждый из трех вольтметров :

-  1) Пиковый вольтметр (ПВ) с открытым входом показывает амплитудное значение напряжения

            UПВ = Um = 2 В

      Так как в задании неясно , как проградуирован пиковый

       вольтметр , необходимо дополнить , что если градуировка

       выполнена в среднеквадратических значениях синусоидального

       напряжения то показания составят (формула 5.11. [1]) :

            UПВ = 0,707Um = 1,41 В

-  2) Вольтметр средневыпрямленных значений (СВ) с закрытым

      входом , проградуированный в среднеквадратических значениях

      синусоидального напряжения , согласно 5.10 и 5.13 [1] , будет  

      иметь показания :

             UСВ = Кф sin (Uср.в - Uпс) = 1,11(Uср.в - Uпс)

      Подставляем значения Uср.в и Uпс для заданного напряжения :

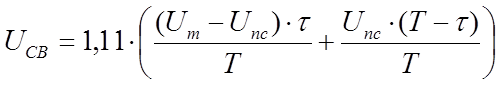      В данное выражение подставляем :

 

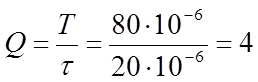–  скважность импульсов ;