






По каждой задаче необходимо составить программу, отладить ее, провести расчет и в отчете по курсовой работе привести условие задачи, собрать блок-схему, программу ее решения и распечатку результатов счета.
Задача №1
Напряжение в электрической цепи описывается уравнением:
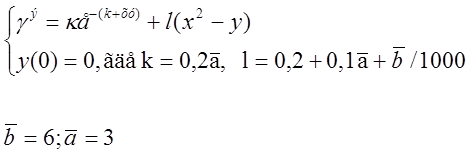
Определить количество теплоты, выделяющегося на единичном сопротивлении за единицу времени. Количество теплоты определяется по формуле:
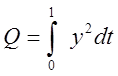
Дифференциальное уравнение решить методом Рунге-Кутта с точностью 10-3.
Интеграл вычислить по формуле Симпсона с шагом 0.1. Для нахождения значений функции в промежуточных узлах применить линейную интерполяцию.
Задача №2
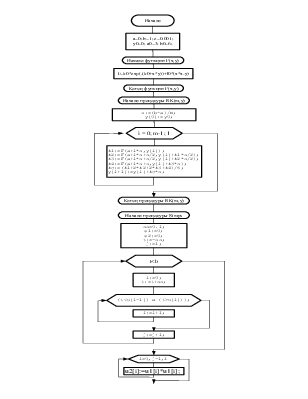
а) Для задачи Коши составить программу по блок-схеме и проверить правильность ее работы на тестовом примере, где полагаем:
y/=f(x,y)=x,
Решением должна быть таблица:
x y
____________
0 0
h y1
1 0,5
Значение y=0,5 при х=1 является показателем правильности работы этой части программы. Поскольку значения х составляют массив U, а значения y-массив U2, то данные этих массивов и следует проверять при решении тестового примера. После успешной проверки переходим к решению задачи №1 и получаем уже для этой задачи искомые массивы U и U2.
б) С помощью интерполирования и данных массива U2 получаем таблицу (при этом, значения у и составляют массив U2):
x y
____________
0 у0
0.1 y(0.1)
1 у(1)
Значения у этой таблицы получены уже с шагом h=0.1
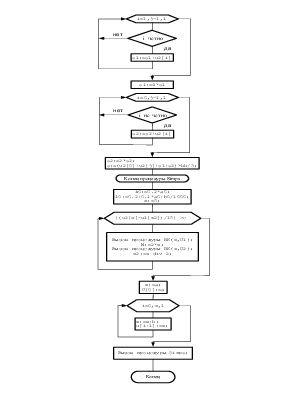
в) Возводим полученные у в квадрат и используем, затем, в программе метода Симпсона для получения искомого значения интеграла. Программу следует составить в соответствии с блок-схемой, где N=10,h=0.1, а в блоке 4 как раз и следует получить у2, положив уi: yi2
Значения уi в правой части этого соотношения получены в б).
РЕШЕНИЕ
Задача № 1
Текст программы:
Program Zadacha1;
Uses CRT;
Const
a=0; {a,b - начало и конец интервала }
b=1;
e=0.001; {погрешность}
y0=0; {начальное условие Коши}
a0=3; {данные варианта }
b0=6; {данные варианта }
TYPE
mas=array [0..1000] of real;
Var
k0,l0:real;
x,h:real;
i,m,m2:integer;
L:boolean;
U,U1,U2:mas;
{--------------------------------------------------------------------}
{данная функция описывает диф. урав-е }
FUNCTION F(x,y:real):real;
Begin
F:=k0*exp(-(k0+x*y))+l0*(x*x-y);
End;
{--------------------------------------------------------------------}
{эта процедура осуществ-т алгоритм Рунге-Кутта}
Procedure RK(m:integer; var y:mas);
var k1,k2,k3,k4,kc:real;
begin
h:=(b-a)/m;
y[0]:=y0;
for i:=0 to m-1 do
begin
k1:=F(a+i*h,y[i]); {формулы алг-ма Р-Кутта}
k2:=F(a+i*h+h/2,y[i]+k1*h/2);
k3:=F(a+i*h+h/2,y[i]+k2*h/2);
k4:=F(a+i*h+h,y[i]+k3*h);
kc:=(k1+2*k2+2*k3+k4)/6;
y[i+1]:=y[i]+kc*h;
end;
end;
{--------------------------------------------------------------------}
{эта процедура осущест-т метод Симпсона для нахождения интеграла Q}
Procedure Simps;
const hh=0.1; {шаг по условию задачи}
var
t,s1,s2,s:real;
i,j:integer;
begin
s1:=0;
s2:=0;
t:=-hh;
j:=1;
writeln('проинтерполированная ф-я');
{а этом цикле осущ-ся алгор. линейной интерполяции
для нахождения промежуточных точек ф-ии }
repeat
i:=0;
t:=t+hh;
repeat
i:=i+1;
until ((t>=u[i-1]) and (t<=u[i])); {нахождение подинтервала}
u1[j]:=((u2[i]-u2[i-1])*(t-u[i-1]))/(u[i]-u[i-1])+u2[i-1];
writeln('x= ',t:4:4,' y= ',u1[j]:4:4);
j:=j+1;
until t>=b;
for i:=1 to (j-1) do u2[i]:=u1[i]*u1[i];
{в этом цикле находится сумма всех значений ф-ии с четными индексами}
for i:=1 to (j-1) do
begin
if odd(i)=false then s1:=s1+u2[i];
end;
s1:=4*s1;
{в этом цикле находится сумма всех значений ф-ии с нечетными индексами}
for i:=0 to (j-1) do
begin
if odd(i) then s2:=s2+u2[i];
end;
s2:=2*s2;
s:=(u2[0]+u2[j]+s1+s2)*hh/3; {формула Симпсона}
writeln('интеграл равен');
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.