Составление программы, вычисляющей силу тока

Вариант IX

Задание

Изменение заряда (Y) на некотором конденсаторе описывается дифференциальным уравнением:

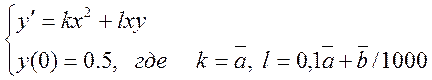
Для данного варианта a=3, b=9.

Составить программу, вычисляющую силу тока 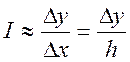при x=0.05, x=0.1, x=0.15 … x=0.95.

Указание: дифференциальное уравнение решить методом Рунге-Кутта с точностью 10^-3. Разность Δy вычисляется для тех интервалов Δx=h, которые заключают в себе указанные точки x=0.05, x=0.1, … x=0.95. Представить распечатку заряда y для ; y’ и I для .

Решение

1-й этап. Для решения задачи Коши методом Рунге-Кутта запишем подпрограмму. Вычисление значения производной в определённых точках оформим через отдельную функцию:

function f(a,b:real):real;

begin

   f:=3*sqr(a)-0.309*a*b;{f:=a;{ proverka }

end;

procedure RungeKutt(var u1,v1:massiv);

var i:integer;

begin

     h:=0.2;

     for i:=1 to n+1 do

     begin

          k1:=h*f(u1[i],v1[i]);

          k2:=h*f(u1[i]+0.5*h,v1[i]+0.5*k1);

          k3:=h*f(u1[i]+0.5*h,v1[i]+0.5*k2);

          k4:=h*f(u1[i]+h,v1[i]+k3);

          v1[i+1]:=v1[i]+(k1+2*k2+2*k3+k4)/6;

          u1[i+1]:=u1[i]+h;

     end; end;

Осуществляем проверку на тестовом примере, где полагаем: .5. При запуске программы получаем:

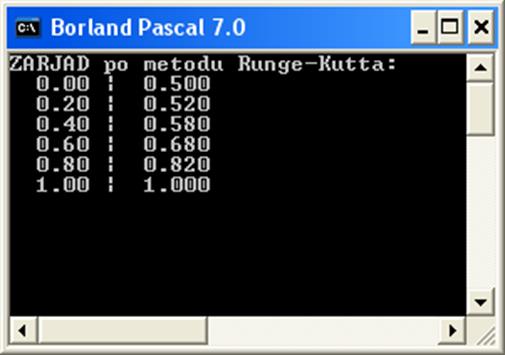
Рис.1. Тестирование программы, реализующей метод Рунге-Кутта

Значение y=1 при x=1 является доказательством правильности работы программы.

Теперь в функции указываем формулу производной из задачи. Получаем следующие результаты:

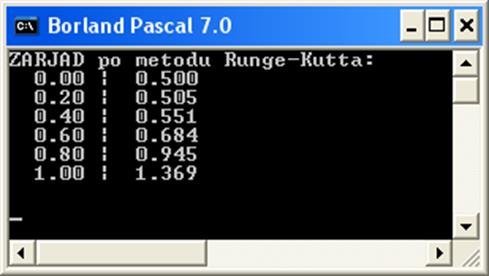
Рис.2. Значения заряда y

2-й этап. С помощью интерполирования в точках z_k=0.05; 0.1; 0.15; …; 0.95, где требуется вычислить производную y’, находим соответствующие значения y_k с шагом h=0.05 и вычисляем эту производную по формуле заданной в варианте (вызываем функцию f). Интерполирование заключено в процедуру Lagrange:

procedure Lagrange(u1,v1:massiv; var x,y:massiv);

var i,j:integer;

begin

     for i:=2 to n do

     begin

          x[i]:=x[i-1]+h;

          for j:=1 to n do

          begin

          if x[i]=u1[j] then

             begin             y[i]:=v1[j];             break;end else

          if (x[i]>u1[j])and(x[i]<u1[j+1]) then begin

             y[i]:=v1[j]*(x[i]-u1[j+1])/(u1[j]-u1[j+1])+

                   v1[j+1]*(x[i]-u1[j])/(u1[j+1]-u1[j]);

             break;end;

          end;     end; end;

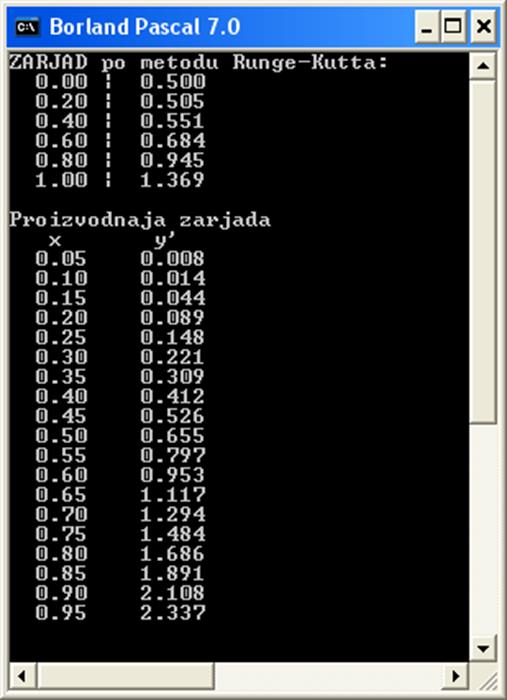
Рис.3. Вычисление производной заряда

3-й этап. С помощью интерполирования в точках t_k=0.025; 0.075; 0.125; …; 0.975, находим соответствующие y_k. Вычисляем теперь производную y’ в точках z_k=0.05; 0.1; 0.15; …; 0.95 по формуле 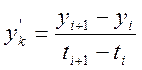; причём, для каждой точке z_k сначала определяем интервал (t_i; t_i+1) такой, что t_i<z_k<t_i+1, т.е. содержащий z_k, а затем применяем формулу 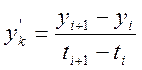 для данного z_k.. В итоге получаем следующую программу и результаты:

Общая программа:

uses crt;

type massiv=array[1..100] of real;

var t,a,b,h,k1,k2,k3,k4:real;

    i,j,l,n:integer;

    x,y,u,v,x2,y2:massiv;

    q:char;

function f(a,b:real):real;

begin

   f:=3*sqr(a)-0.309*a*b;{f:=a;{ proverka }

end;

procedure RungeKutt(var u1,v1:massiv);

var i:integer;

begin

     h:=0.2;

     for i:=1 to n+1 do

     begin

          k1:=h*f(u1[i],v1[i]);

          k2:=h*f(u1[i]+0.5*h,v1[i]+0.5*k1);

          k3:=h*f(u1[i]+0.5*h,v1[i]+0.5*k2);

          k4:=h*f(u1[i]+h,v1[i]+k3);

          v1[i+1]:=v1[i]+(k1+2*k2+2*k3+k4)/6;

          u1[i+1]:=u1[i]+h;     end;

end;

procedure Lagrange(u1,v1:massiv; var x,y:massiv);

var i,j:integer;

begin

     for i:=2 to n do

     begin

          x[i]:=x[i-1]+h;

          for j:=1 to n do

          begin

          if x[i]=u1[j] then

             begin

             y[i]:=v1[j];

             break;end else

          if (x[i]>u1[j])and(x[i]<u1[j+1]) then begin

             y[i]:=v1[j]*(x[i]-u1[j+1])/(u1[j]-u1[j+1])+

                   v1[j+1]*(x[i]-u1[j])/(u1[j+1]-u1[j]);

             break;end;

          end;     end;

end;

procedure SilaToka(u1,v1:massiv; var x,y:massiv);

var i,j:integer;

begin

     x[1]:=0.05;

     for i:=2 to n do

     begin

          x[i]:=x[i-1]+h;

          for j:=1 to n do

          begin

          if x[i]=u1[j] then

             begin    y[i]:=v1[j];        break;end else

          if (x[i]>u1[j])and(x[i]<u1[j+1]) then begin

             y[i]:=(v1[j+1]-v1[j])/(u1[j+1]-u1[j]);

             break;end;

          end;     end;

end;

begin

     clrscr;

     n:=5;      v[1]:=0.5;     u[1]:=0;

     writeln('ZARJAD po metodu Runge-Kutta: ');

     u[1]:=0;v[1]:=0.5;

     RungeKutt(u,v);

     for i:=1 to n+1 do

          writeln(u[i]:6:2,' |',v[i]:7:3);

     n:=19;

     writeln;     writeln('Proizvodnaja zarjada');     writeln('x':4,'y':8,#39);

     h:=0.05;

     x2[1]:=0.05;

     Lagrange(u,v,x2,y2);

     for i:=1 to n do

       writeln(x2[i]:6:2,f(x2[i],y2[i]):9:3);     writeln;

     writeln('Sila toka I');     u[1]:=0.025;

     RungeKutt(u,v);

     SilaToka(u,v,x2,y2);

     for i:=1 to n do

       writeln(x2[i]:6:2,f(x2[i],y2[i]):9:3);

     readln; end.

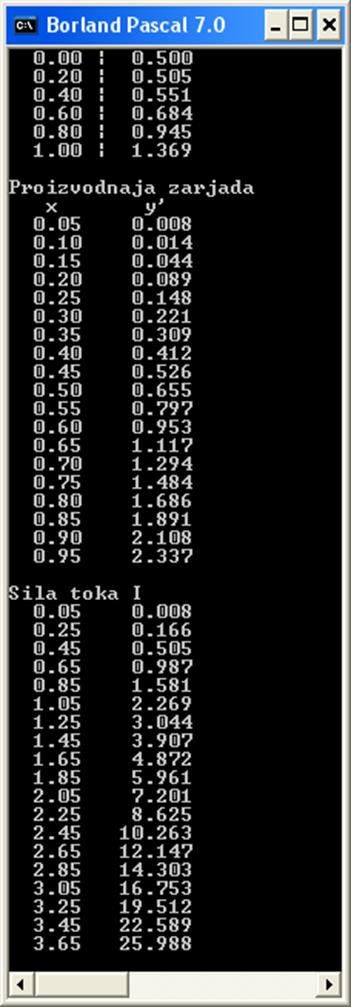
Рис.4. Результат работы программы: заряд y, производная заряда и сила тока