








Государственный комитет РФ по связи и информатизации
Сибирский государственный университет телекоммуникаций и информатики
По предмету : Информатика
Студент 2 курса группа М-52 заочной формы подготовки специалистов по сокращенной программе
Преснецов Сергей Юрьевич
Работа выполнена : «___»____________200___г.
________________________________________________________________________
Оценка _________________________ «___» _____________200___г.
Преподаватель_____________________________________________
Новосибирск
2007 г.
Напряжение в электрической цепи описывается уравнением
![]() 2. y' = 1 – sin (kx
+ y) + (Iy)/(2 + x) (1)
2. y' = 1 – sin (kx
+ y) + (Iy)/(2 + x) (1)
y(0) = 0 , где k = 1 + ![]() /4 , I = - 0,3 + 0,2
/4 , I = - 0,3 + 0,2![]() +
+ ![]() /1000 (2)
/1000 (2)
где а=3, b=3.
Определить количество теплоты , выделяющегося на единичном сопротивлении за единицу времени . Количество теплоты определяется по формуле :
![]() T
T
Q = y² dt
1-й этап .
Для задачи Коши составляем программу по блок-схеме (рис.1) и проверяем , сначала правильность ее работы на тестовом примере , где полагаем :
y' = ƒ (х , у) = х ,
у(0) = 0
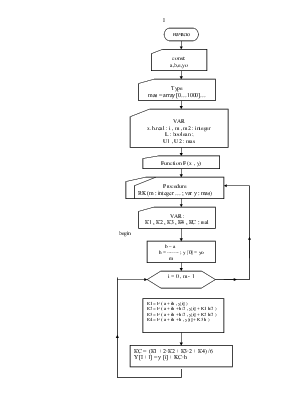
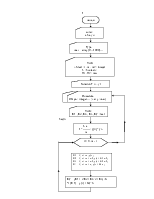
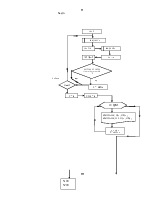
Блок-схема дифференциального уравнения 1-го порядка методом Рунге-Кутта
1
I
![]()
![]()
![]()
![]()
![]()
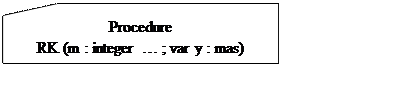

|


 |
begin
 |
|||
![]()
![]() II
II
begin
|
|
|
|
|
![Ромб: | U2[M] –U1[M2] |
----------------------- >e
15](https://files3.vunivere.ru/workbase/00/01/87/49/images/image022.gif)

|
|
|

![Блок-схема: документ: WRITELN ( U[i] , U2[i] )
WRITELN (FF1. U[i] , U2[i] )](https://files3.vunivere.ru/workbase/00/01/87/49/images/image025.gif)
|
|
|

|
|
|
|||
 |
|||
 |
|||
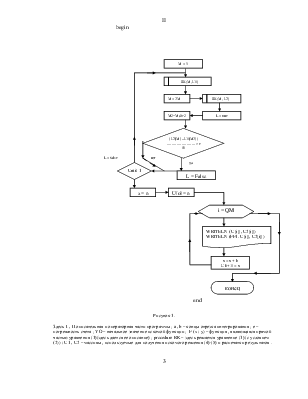
Рисунок 1.
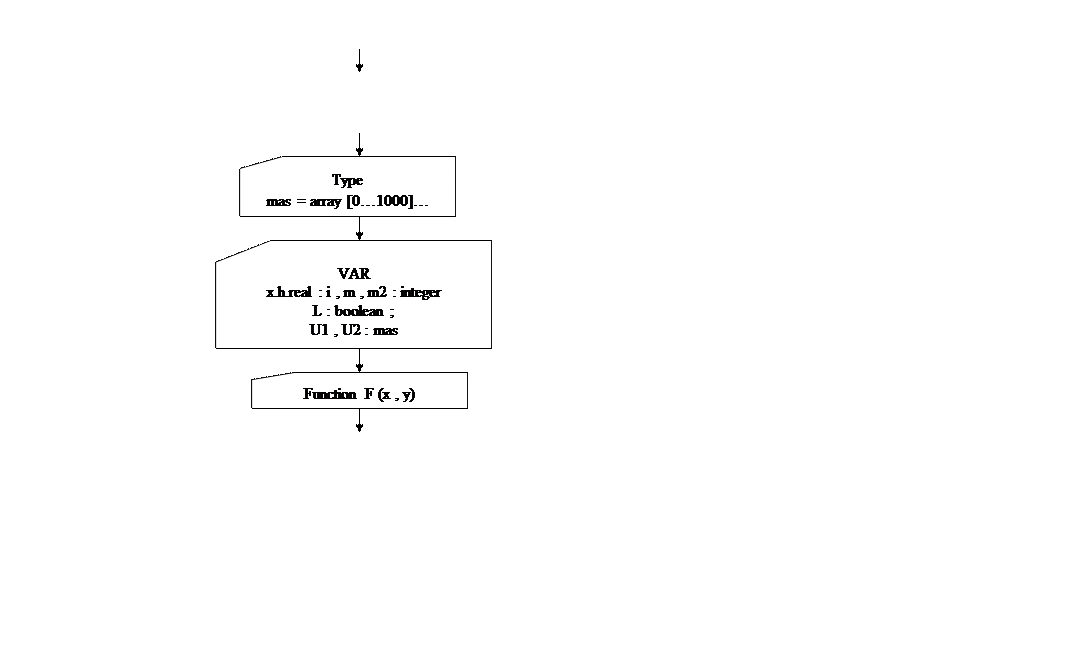
Здесь I , II описательная и операторная части программы ; a , b – концы отрезка интегрирования ; е – погрешность счета ; YO – начальное значение искомой функции ; F (x ; y) – функция , являющаяся прямой частью уравнения (1)(здесь дается ее описание) ; procedure RK – здесь решается уравнение (1) (с условием (2)) ; U1 , U2 – массивы , используемые для получения искомого решения (4)-(5) и распечатки результатов .
3
Программа 1-го этапа
uses crt;
type mas=array[0..1000] of real;
const a=0;
b=1;
y0=0;
e=0.001;
var
h:real;
u1,u2:mas;
i,m,m2:integer;
l:boolean;
function f(x,y:real):real;
begin
f:=x;
end;
procedure RK(m:integer; var y:mas);
var
k1,k2,k3,k4,kc:real;
i:integer;
begin
h:=(b-a)/m;
y[0]:=y0;
for i:=0 to m-1 do
begin
k1:=f(a+i*h,y[i]);
k2:=f(a+i*h+h/2,y[i]+k1*h/2);
k3:=f(a+i*h+h/2,y[i]+k2*h/2);
k4:=f(a+i*h+h,y[i]+k3*h);
kc:=(k1+2*k2+k3*2+k4)/6;
y[i+1]:=y[i]+kc*h;
end;
end;
begin
clrscr;
m:=1;
repeat
rk(m,u1);
m:=m*2;
rk(m,u2);
l:=true;
m2:= m div 2;
if (abs(u2[m]-u1[m2])/15)>e then l:=false;
4
until l;
writeln(' X Y');
for i:=0 to m do
writeln(i*h:5:1,' ', u2[i]:5:2);
readln;
end.
Результат выполнения:
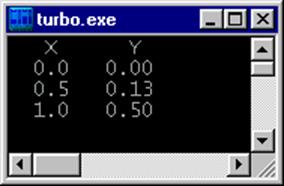
Значение у = 0,5 при х = 1 является показателем правильности работы этой части программы.
Далее, модифицируем функцию f под наши условия задачи Коши и примем m=5.
function f(x,y:real):real;
const a=3;
b=3;
var k,i:real;
begin
k:=1+a/4;
i:=-0.3+0.2*a+b/1000;
f:=1-sin(k*x+y)+(i*y)/(2+x);
end;
Результат выполнения:
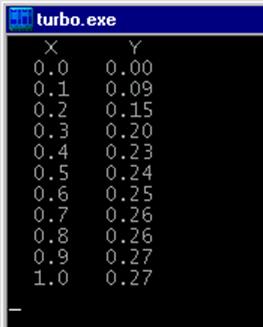
А это означает, что решение, удовлетворяющее заданной точности 0,001, найдено при m=10, т.е. шаг h=0.1.
5
2-й этап.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.