Определение количества теплоты, выделяющегося на единичном сопротивлении за единицу времени, страница 2

В массиве U2  мы имеем значения искомой функции, полученной при изменении аргумента с шагом 0,1, соответственно, выполнение этапа №2, т.е. интерполирования с шагом аргумента 0,1, бессмысленно, т.к. требуемый результат после выполнения этапа №2 в нашем случае уже достигнут на этапе №1.

3-й этап.

Возводим полученные у в квадрат и используем , затем , в программе метода Симпсона для получения искомого значения интеграла.

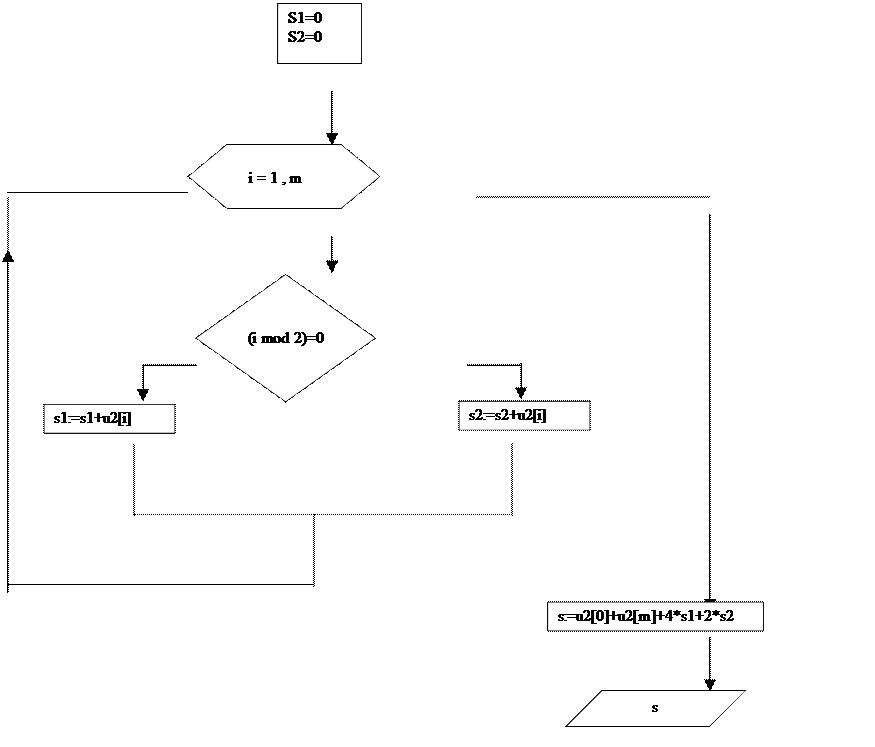
Приведем участок программы и блок-схемы, реализующие вычисление искомого интеграла.

s1:=0;s2:=0;

for i:=1 to m do

u2[i]:=sqr(u2[i]);

for i:=1 to m-1 do

begin

if (i mod 2)=0 then s2:=s2+u2[i]

else  s1:=s1+u2[i]

end;

s:=u2[0]+u2[m]+4*s1+2*s2;

writeln('Количество теплоты - ',s:5:2);

6

 

Объединяя результаты этапов 1-3 приведем итоговые блок-схему и программу.

Блок-схема дифференциального уравнения 1-го порядка методом Рунге-Кутта

7

I

b – a h = ------- ; y [0] = yo               m

К1 = F ( a + ih , y[i] ) К2 = F ( a + ih + h/2 , y[i] + K1 h/2 ) К3 = F ( a + ih + h/2 , y[i] + K2 h/2 ) К4 = F ( a + ih + h , y[i] + K3 h )

КС =  (К1 + 2·К2 + К3·2 + К4) /6 Y [I +1] = y [i] + KC·h

 

                                              begin

 

II

                                            begin

RK(M, U1)

M = 2M

RK(M, U2)

M2=Mdir·2

L = true

L = False

x = n

U[o] = n

x = x + h U [i+1] = x

L = false

нет

да

	M = 5

 

III

 

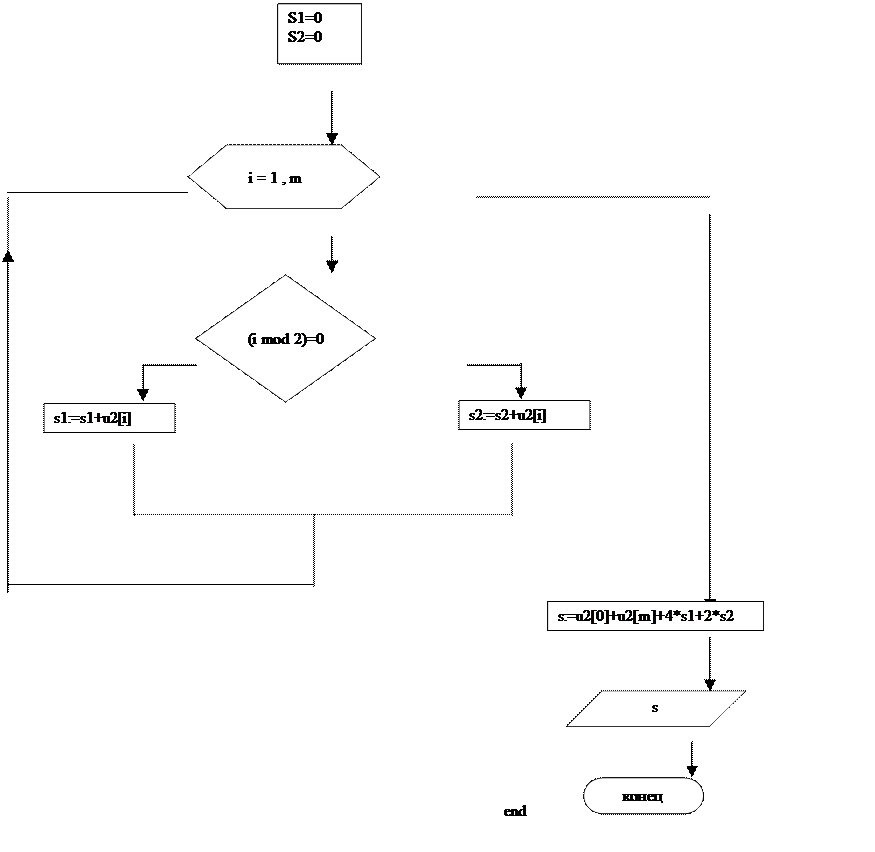Здесь I ,  II описательная и операторная части программы, реализующие метод Рунге-Кутта; a , b – концы отрезка интегрирования ; е – погрешность счета ; YO – начальное значение искомой функции ;  F (x ; y) – функция , являющаяся прямой частью уравнения; procedure RK – здесь решается уравнение (1) (с условием (2)) ; U1 , U2 – массивы , используемые для получения искомого решения; III – операторная часть, реализующая метод Симпсона, вычисления интеграла; m-количество разбиения (четное = 10); s1- сумма нечетных слагаемых, s1- сумма четных слагаемых, s – итоговое значение интеграла.

10

Итоговая программа

uses crt;

type mas=array[0..1000] of real;

const a=0;

      b=1;

      y0=0;

      e=0.001;

var

h:real;

u1,u2:mas;

i,m,m2:integer;

l:boolean;

s,s1,s2:real;

function f(x,y:real):real;

const a=3;

      b=3;

var k,i:real;

begin

k:=1+a/4;

i:=-0.3+0.2*a+b/1000;

f:=1-sin(k*x+y)+(i*y)/(2+x);

end;

procedure RK(m:integer; var y:mas);

var

k1,k2,k3,k4,kc:real;

i:integer;

begin

h:=(b-a)/m;

y[0]:=y0;

for i:=0 to m-1 do

begin

k1:=f(a+i*h,y[i]);

k2:=f(a+i*h+h/2,y[i]+k1*h/2);

k3:=f(a+i*h+h/2,y[i]+k2*h/2);

k4:=f(a+i*h+h,y[i]+k3*h);

kc:=(k1+2*k2+k3*2+k4)/6;

y[i+1]:=y[i]+kc*h;

end;

end;

begin

clrscr;

11

m:=1;

repeat

rk(m,u1);

m:=m*2;

rk(m,u2);

l:=true;

m2:= m div 2;

if (abs(u2[m]-u1[m2])/15)>e then l:=false;

until l;

s1:=0;s2:=0;

for i:=1 to m do

u2[i]:=sqr(u2[i]);

for i:=1 to m-1 do

begin

if (i mod 2)=0 then s2:=s2+u2[i]

else  s1:=s1+u2[i]

end;

s:=u2[0]+u2[m]+4*s1+2*s2;

writeln('Количество теплоты - ',s:5:2);

readln;

end.

Результат работы программы:

12