Анализ сети, заданной схемы. Структурная матрица сети. Определение путей ранга, страница 5

                                                      

где  E_Yi (Y_i) – вероятность  отказов  в  полнодоступном  пучке  при  поступлении  пуассоновского  потока  и  экспоненциальном  законе  распределения  времени  обслуживания  (первая  формула  Эрланга).

                Для  i – го  пучка  каналов  имеем:

                                                        

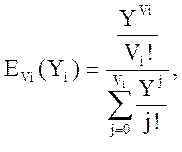
где  Y_i – интенсивность  поступающей  на  пучок  нагрузки;

        V_i – число  каналов  в  пучке.

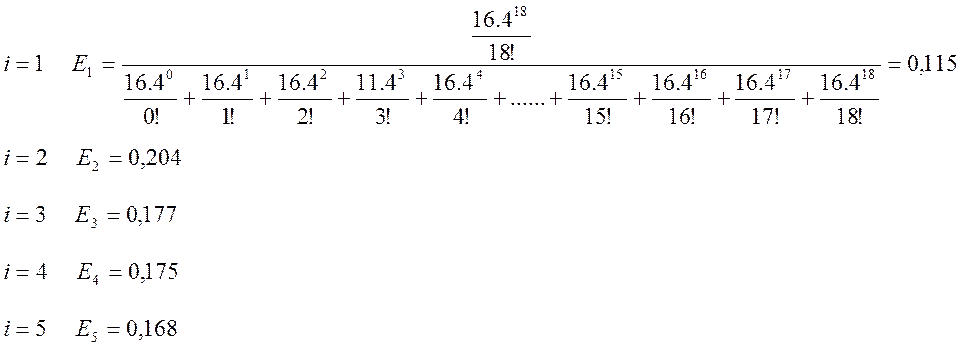
Расчет  математического  ожидания  избыточной  нагрузки:

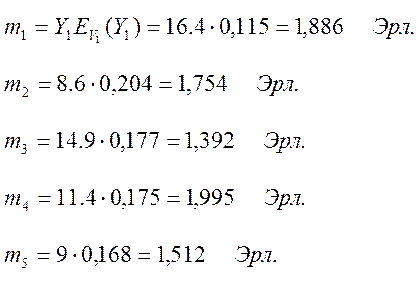
Для  случая  а)  считаем,  что  избыточные  потоки  от  пяти  первичных  пучков  являются  пуассоновскими.  Определяем  интенсивность  потока  на  обходное  направление:

              Теперь  получаем  схему  для  расчета  обходного  направления.  Зная  норматив  вероятности  отказов  на  обходном  направлении  (0.01)  и  величину  интенсивности  (М)  можно  найти  величину  V_обх.  по  номограмме  Эрланга-Пальма.

V_обх.» 19  каналов. 

               б)  Для  каждого  избыточного  потока  вычисляем  математическое  ожидание  нагрузки  m_i  по  формуле:          m_i = Y_iE_Vi (Y_i),  что  сделано  в  расчетах  по  п. а)  задания.  Помимо  этого,  определяем  величины  дисперсии  избыточных  нагрузок  от  всех  прямых  пучков:

                               

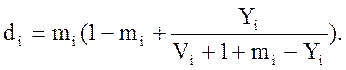
Для  объединенного  избыточного  потока,  поступающего  на  обходное  направление,  имеем:

                              

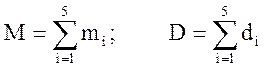
Для  учета  колеблемости  поступающего  потока  при  расчете  числа  каналов  в  обходном  направлении  V_обх  следует  использовать  метод  “эквивалентной  замены”

Рисунок  7.   Vобх   S   YЭ   M, D   mпот   Робх= 0.01

Вилкинсона.  Производим  эквивалентную  замену  пяти  первичных  полнодоступных  пучков  (см.  рис. 6),  на  каждый  из  которых  поступает  нагрузка  интенсивностью  Y_i,  одним  полнодоступным  пучком  емкостью  S  (рис.  7).  Рассматриваем  всю  эту  схему  как  один  полнодоступный  пучок  емкостью  V_обх + S,  на  вход  которого  поступает  эквивалентная  нагрузка  Y_экв.  Расчет  ведем  по  приближенным  формулам:

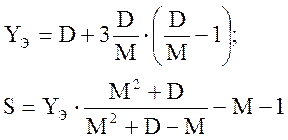
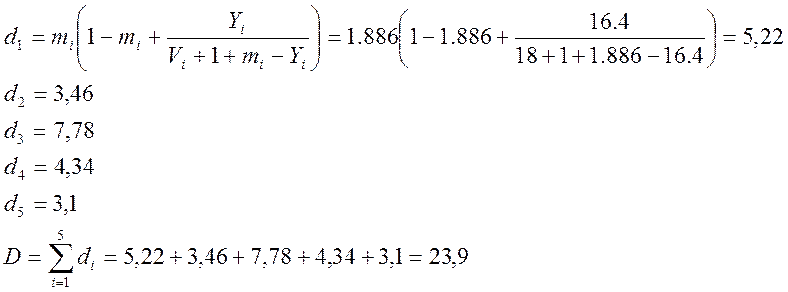
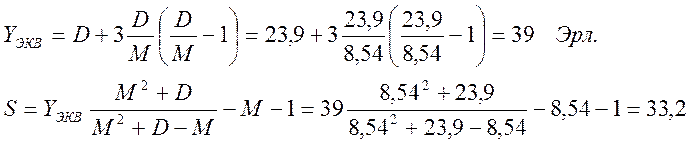
Потери  в  эквивалентной  схеме    можно  рассчитать  по  формуле  (нормативное  значений  потерь  в  обходном  направлении  р _обх.н  известно  и  равно  0.01):

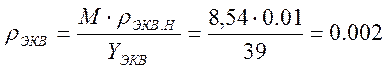
Рассматривая  (S + V_обх)  как  общий  полнодоступный  пучок.  Величину  (S + V_обх)  определяем  по  номограмме  Эрланга-Пальма  » 56  канал.  Зная  число  каналов  в  эквивалентном  пучке,  находим  V_обх.

  канала.

               Вывод:  избыточные  потоки  не  являются  пуассоновскими,  для  которых  характерен  равномерный  характер  поступления  вызовов  и  дисперсия  нагрузки  равна  ее  математическому  ожиданию  m_i = d_i.  Для  избыточного  потока  характерно  неравенство  m_i < d_i,  т.е.  он  характеризуется  наличием  малых  отрезков  времени,  на  которых  имеются  большие  скопления  вызовов,  и  больших  отрезков  времени,  когда  вызова  отсутствуют. 

Список литературы

1.  Теория сетей связи/Под ред. В.Н.Рогинского. – М.: Связь, 1981.

2.  Лазарев В.Г. Электронная коммутация в узлах связи. – М.: Связь, 1974.

3.  Методические указания и контрольное задание по курсу Проектирован и и техническая эксплуатация сетей связи./Сост. Н.Е.Богомолова, Н.П.Маркин, Г.Л.Слепова. 1991.