Анализ сети, заданной схемы. Структурная матрица сети. Определение путей ранга

Министерство связи РФ

Сибирский Государственный университет

телекоммуникаций и информатики

 Контрольная работа по курсу:

Сети связи

студента группы ЗТ-03

                                                                                 заочного факультета АЭС

                                                                                 А. С. Сидоров

Новосибирск – 2002 г.

Вариант №36

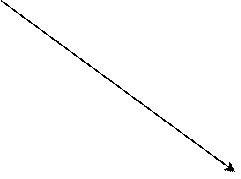
                 Задача  1:             Провести  анализ  сети,  схема  которой  дана  на  рис. 1:

Рис.  1   e   k   h   d   c   a   f   6   5   4   3   1   2   b

1.  Найти  структурную  матрицу  сети

2.  Найти  все  возможные  пути  от  узла  коммутации  УК_i  до  УК_j . Номера  узлов  i – 4,  j – 2,  в  соответствии  с  номером  варианта  0.

3.  Определить  пути  ранга  r  не  более  трех  для  заданной  в  п. 2  пары  УК_i - УК_j.

4.  По  заданной  матрице  построить  дерево  путей  ранга  r  на  более  3  между  УК_i  и  всеми  другими  узлами  сети.  Выделить  в  дереве  путей  пути  с  r < 3  для  связи  с  углом  j  и  сравнить  полученный  результат  с  результатом  п.  1  задания.

5.  Найти  квазисечения  между  УК_i  и  УК_j  для  множества  путей  r < 3.

6.  Определить   вероятность  связности  узлов  коммутации  сети  связи  УК_i  и  УК_j  - ,  если  определено  множество  путей,  которые  могут  быть  использованы  для  связи  между  указанными  УК.  Ограничить  ранг  путей  r < 3.  Решение  провести  для  данных,  указанных  в  п.  2,  используя  результат  решения  п.  3.  Определить  численное  значение  ,  при  условии,  что  вероятности  безотказной  работы  ребер  сети  одинаковы  и  равны  0.9.

                 Решение:   Граф  на  рис. 1  содержит  6  вершин  (УК)  и  9  ребер  (пучков  каналов),  обозначенных  для  кратности  буквами.  Ранг  вершины  (число  ребер,  опирающихся  на  данную  вершину)  в  нашем  случае  не  превышает  4  (4,  2).  Запишем  пути  от  узла  4  к  УК 2:

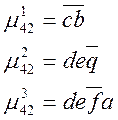
Совокупность  путей  от  УК4  к  УК₂  можно  записать:

Из  m_4,2  можно  выделить  множество  путей,   ранг  которых  будет  не  более  r < 3:

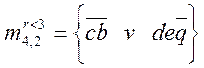
Для  анализа  сети,  т.е.  нахождения  путей  и  сечений,  используют  структурную  матрицу  В.  В – квадратная  матрица,  строки  и  столбцы  которой  сопоставлены  с  узлами  сети.  Связь  внутри  узла  отображается  единицей,  если   связи  между  узлами  нет,  то  элемент  равен  0.

B =		1	2	3	4	5	6
	1	1	a	0	0	0	f
	2		1	b	0	h	q
	3	0		1	c	0	0
	4	0	0		1	d	0
	5	0	0	0		1	e
	6			0			1

Определим  из  из  матрицы  В  m₄₂  и  проведем  разложение  по  ненулевым  членам  четвертой  строки  и  далее:

                

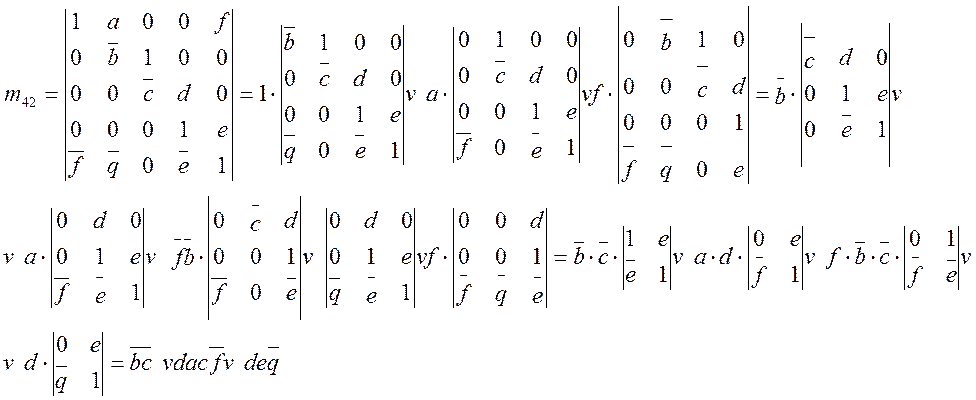
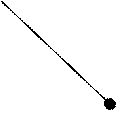
 Графический  эквивалент  перечня  путей – дерево  путей – можно  построить  непосредственно  по  матрице  В.  Для  построения  дерева  путей  из  УК4  берем  4  строку  матрицы  В  и  помечаем  на  графе  вершины  путей  с  r = 1,  имеющие  b_ij ¹ 0.  После  того,  как  процесс  для  строки  закончен  и  отмечены  номера  узлов  (по  номеру  столбца),    переходим  к  строке  одного  из  тех  узлов,     который  расположен  на  линии  r = 1,  и  продолжаем  процесс  аналогичным  образом.  При  этом  следует  учитывать,  что  узлы  в  одном  пути  не  должны  повторятся.   Дерево  путей  для  УК₄  (r < 3)  показано  на  рис.  2.