где 
-допустимая
нагрузка на трубы, определенная по условию сохранения прочности стека; σв.ст –предел прочности стекла; σт –предел текучести материала трубы; n- запас прочности (n
=1,3); Fст , Fтр
- площади поперечного сечения слоя стекла и трубы соответственно; Eст , Eтр –
модули упругости стекла и трубы соответственно.
Покрытие труб эпоксидными смолами и лаками также хорошо защищает их от отложений парафина и солей. Эпоксидные смолы эластичнее стекла, и при деформации труб эпоксидный слой не разрушается. Однако, температура применения покрытий из эпоксидных смол ограничена 80-100 0С.
Эмалированные трубы обладают наиболее прочным покрытием, высокой теплостойкостью, морозоустойчивостью и гладкой поверхностью. Для защиты НКТ от агрессивных сред трубы покрываются несколькими слоями. Однако технология нанесения эмалей значительно сложнее технологии покрытия стеклом и эпоксидными смолами.
По износостойкости силикатные покрытия (эмали и стекла) превосходят полимерные (смолы и лаки).
Термостойкость силикатных покрытий также значительно выше полимерных и составляет 200-600 0С.
Общим недостатком всех покрытий является незащищенность муфтового соединения труб. В этом месте рекомендуется устанавливать эластичные полимерные приставки, перекрывающие незащищенные место, или протекторные кольца, электрический потенциал материала которых значительно ниже потенциала стали.
Пример расчета глубины спуска остекленных труб. Проверить условие равенства относительных удлинений стекла и металла и рассчитать максимальную глубину спуска гладких остекленных НКТ 89х6,5 мм «Д» при фонтанной эксплуатации скважины, если предел прочности стекла составляет 60 МПа.
Решение. Для решения задачи используем формулы (*) и (**). Допустимую нагрузку на остекленные трубы определим по формуле (**), полагая, что по технологии изготовления средняя толщина слоя стекла составляет 1 мм.
Тогда Fтр=0,785(892-762)·10-6=1,684·10-3 м2 ;
Fст =0,785(762-742)·10-6=0,236·10-3 м2 ;
Допустимая нагрузка
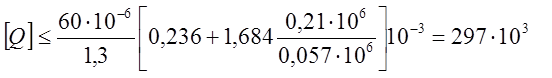Н,
Допустимая глубина спуска без учета облегчения в жидкости составит
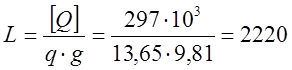м. Здесь –весь
1м остекленной трубы в кг
5.5. Расчеты насосно-компрессорных труб
Расчет тонкостенных труб на внутреннее давление
Трубу следует
считать тонкостенным, если толщина его стенки меньше одной десятой (0,1)
внутреннего диаметра трубы, т.е. 
При расчете тонкостенных труб предполагается, что в окружном (тангенциальном) направлении напряжения постоянны по толщине стенки, а в радиальном вообще отсутствуют.
Допустим, имеем отрезок трубы длиной l, внутренним диаметром Dв, толщиной стенки δ, внутри которого действует давление p. Сила, стремящаяся разорвать этот отрезок трубы по меридианной плоскости,
,
(5.1)
Сила
прочностного сопротивления стенок трубы N определяется
ее размерами (δ, l)
и прочностной характеристикой материала (
):
(5.2)
Из условия равновесия системы
сил, т.е. 
или 
,
откуда
,
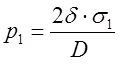(5.3)
или
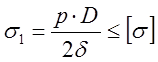
Здесь σ1 – окружное (тангенциальное) напряжение, возникающее в меридианной плоскости от давления p; D – cредний диаметр трубы.
При σ1 = σт давления p1 является разрушающим. Для определения допускаемого давления рдоп необходимо вместо σ1 подставить σдоп.
Под действием внутреннего давления создаются также продольные напряжения σ2.
,
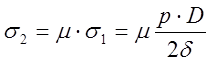(5.4)
где μ - коэффициент Пуассона (для стали всех марок μ=0,3).
,
(5.6)
и окружное (тангенциальное) напряжение
,
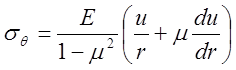(5.7)
Радиальное удлинение тела трубы от действия внутреннего давления u находим из уравнения Эйлера
,
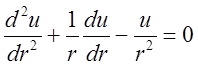или
,
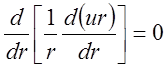Интегрируя его по r последовательно два раза, найдем общее решение уравнения
,
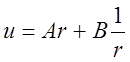(5.8)
Подставляя решение (5.8) в формулы (5.6) и (5.7), получим
,
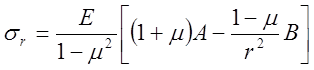(5.9)
,
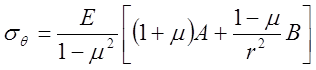(5.10)
Постоянные интегрирования А и В находим из условий для
на внутренней и наружной
поверхностях трубы:
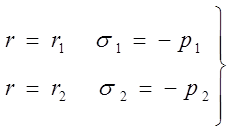(5.11)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.