Вертикальная составляющая силы давления на криволинейную стенку = весу тел давления Фв= G= ρ g Vт.д. , если направление вертикальной составляющей совпадает с направлением веса то она считается действительной, иначе мнимой.
Ф=√ Фx²+Фy²+Фz² , Ф=√ Фx²+Фz² =√ Фг²+Фв²
З-н Архимеда как частный случай силы давления на стенку криволинейного тела
3
на тело, погруженное в жидкость действует сила = весу ж-ти заключённой в погруженном теле.
Кинематика ж-ти
Основные понятия и определения
Движение ж-ти в пространстве носит очень сложный характер и м/б представлено в виде поля скоростей. Движение ж-ти бывает установившимся и неустановившимся. При неустановившимся движении υ и Р зависят от времени U=f1(x,y,z,t), P=f2(x,y,z,t) в установившемся не зависят от времени U=f1(x,y,z), P=f2(x,y,z). Движение м/б 3-х, 2-х или одно- мерным. Движение бывает напорное, безнапорное и свободное:
Напорное – весь канал ж-ти нах-ся под давлением
Свободное – вытекание ж-ти, движение струёй
Струи бывают свободными и затопленными(под уровнем ж-ти)
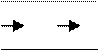
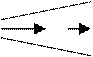Установившееся одномерное движение делится на
равномерное и не равномерное.
U1 = U2 U1>U2
Движение бывает вихревое и потенциальное
Линия тока – линия в каждой точке к-рой вектор скорости направлен по касательной
 |
При неустановившемся движении вид линии тока меняется каждое мгновение, при установившемся – совпадает с траекторией частицы.
Поверхность тока - поверхность, образованная линиями тока, замкнутый контур образованный поверхностями тока н-ся трубкой тока. Трубка тока с бесконечно малым сечением это элементарная струйка.
1. т.к. S бесконечно мало то Р, ρ и U в каждой точке сечения (живого) можно считать const.
2. т.к. элементарная струйка образована линиями тока и векторы скорости направлены по касательной частицы ж-ти не могут входить в неё и выходить ч/з боковую поверхность.
Совокупность элементарных струек образует поток. Живым сечением элементарной струйки( потока) н-ся сечение в каждой точке которого вектор U направлен по нормали. Если элементарная струйка расходится нужно провести сечения ┴ векторам скорости
Элементарный расход – кол-во ж-ти протекающее в единицу времени ч/з живое сечение элементарной струйки dQ Q=[м3/с] – объёмный ρQ=Qм [кг/с] – массовый ρgQ=QВ [Н/с] – весовой.
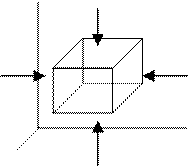Для
расчета каналов не круглого сечения используют понятие гидравлического радиуса
и характерного размера. Гидравлическим радиусом наз-ся отношение живого сечения
потока к длине смоченного периметра RГ=S/X
4
Pz+1/2 ∂P/∂z dz
Px-1/2 ∂P/∂x dx Px+1/2 ∂P/∂x dx
● M
Pz-1/2 ∂P/∂z dz
для этого состояния выведено дифференциальное ур-ие покоя ж-ти, используя принцип Даламбера, перейдём от состояния покоя к состоянию движения, для этого добавим силы инерции
5
сумма 3-х удельных энергий (соотнесённых к единице веса): удельная энергия положения, удельная кинетическая энергия, удельная потенциальная энергия давления есть величина постоянная вдоль потока = гидравлическому напору.
Для элементарной струйки невязкой ж-ти ур-ие Бернулли выражает з-н сохранения мех-ой энергии.
z- нивелирная высота
P/ρg- пьезометрическая высота
U2/2g- высота скоростного напора
6
сумма 3-х высот есть величина постоянная = высоте гидродинамического напора
7
средней скоростью наз-ся такая скорость при к-рой ч/з живое сечение струйки или канала проходит то же к-во ж-ти что и при действительной скорости
не вязкая вязкая ж-ть υS=const
 |
 |
уравнение Бернулли для струйки вязкой ж-ти
при движении вязкой ж-ти вследствие трения ж-ти о стенки канала и слоёв ж-ти друг с другом происходит частичный переход механической энергии в тепловую, к-рая рассеивается и обратно не возвращается – процесс диссипации или рассеивания энергии, поэтому по направлению движения энергия ж-ти уменьшается, в этом случае ур-ие Бернулли наз-ся балансом механической энергии.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.