Физика \ Гидравлика

Гидравлика. Свойства жидкости. Силы действующие в жидкости. Гидростатическое давление и его свойства. Кинематика жидкости, страница 2

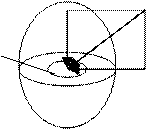
                             dФ                                dN           dФ- сила давления

                                                                                  dT-сила трения

                                                                          dN- результирующая сила

      dS                                                                     dФ/dS=Р lim dФ/dS=Р

                                                                               – давление в точке

                                                                  dT          Ф/S=Рср dТ/dS= τ

                                                                         – касательные напряжения

                                                                                    трения

                                                                Т/S= τср – среднее касательное  

                                                               напряжение по поверхности

гидростатическое давление и его свойства

1. (следует из определения ж-ти) гидростатическое давление в точке направлено по нормали к поверхности соприкосновения объёмов ж-ти и яв-ся сжимающим, т.е. направлено вовнутрь выделенного объёма.

2. величина гидростатического давления в точке не зависит от ориентации площадки в пространстве, на к-рую действует это давление. n – нормаль к АВС

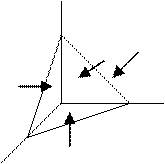                      z  B

                                      Pn       Py

          Px             dz

                                 dx                      x

                  dy                                C

        A                       Pz

y

Заменим действие окруж. силы силами давления, так же действуют силы тяжести

Поскольку элементарный объём нах-ся в покое сумма действ. на него сил =0

Запишем условия равновесия объёмов в проекции на оси координат: х: Px*1/2 dy dz- Pn SABC cos(n,x) + Ix*1/6 dx dy dz =0   SABC cos(n,x)=1/2 dy dz   Px - Pn + Ix*1/3 dx =0 (dx→0)

 Px - Pn =0  Px = Pn , Py = Pn , Pz = Pn , Px = Py= Pz = Pn

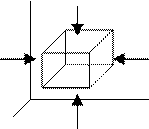3. величина гидростатического давления в точке зависит от плотности ж-ти и глубины погружения под свободную поверхность

                                                        Pz+1/2 ∂P/∂z  dz

Px-1/2 ∂P/∂x dx                                            Px+1/2 ∂P/∂x dx

                                                    ● M

                                                        Pz-1/2 ∂P/∂z dz 

В т.М действует сила давления и сила тяжести. Выделенный объём нах-ся в равновесии. Запишем условия равновесия в проекции на оси координат (Px-1/2 ∂P/∂x dx) dy dz – (Px+1/2 ∂P/∂x dx) dy dz + Ix ρ dx dy dz =0  -∂P/∂x dx dy dz + Ix ρ dx dy dz =0

-∂P/∂x + Ix ρ =0– (3)уравнение Эйлера для покоящейся ж-ти, перейдём к диф.ур-ям, помножим каждое ур-ие на dx, dy, dz и сложим –(∂P/∂x dx+ ∂P/∂y dy+ ∂P/∂z dz)+ ρ(Ix dx+ Iy dy+ Iz dz)=0, -dP+ ρ(Ix dx+ Iy dy+ Iz dz)=0 –уравнение в полных дифференциалах

поверхности, обладающие равным потенциалом наз-ся эквипотенциальными или поверхности уровня

поверхность давления вдоль к-рой давление остаётся одинаковым – поверхность равного давления Р=const, dP=0,   Ixdx+ Iydy+ Izdz=0 – поверхность равного давления

частные случаи решения ур-ия:

1) ж-ть нах-ся в поле силы тяжести

 Основной з-н гидростатики

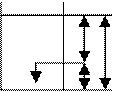          Р0

                                             h

                            M                             z0

                      G                 z

-dP+ ρ(Ix dx+ Iy dy+ Iz dz)=0, Ix=0, Iy=0, Iz= -g , -dP-ρ g dz=0 ∫dP=-ρ g ∫dz  P=-ρ g z+C при z=z0, P=P0, P0=-ρ g z0+C , C= P0+ ρ g z0, P= P0+ρ g (z0-z)=  P0+ρ gh, Основной з-н гидростатики: гидростатическое давление в точке складывается из внешнего давления P0 и весового давления ρ g h

сумма внешнего и весового давления относительно плоскости сравнения будет одинаковым для всех точек ж-ти

З-н Паскаля: внешнее давление передаётся ж-тью во все стороны одинаково

2) Относительный покой ж-ти в сосуде совершающего прямолинейное, равноускоренное движение

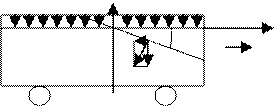       P0                             z

                                            X

                                                 а                       α            а

Скачать файл