Гидравлика. Свойства жидкости. Силы действующие в жидкости. Гидростатическое давление и его свойства. Кинематика жидкости, страница 3

                                                  I            g

-dP+ ρ(I_x dx+ I_y dy+ I_z dz)=0, I_x=-а, I_y=0, I_z= -g , dP= -ρ(а dx+ g dz), P= -ρ а x- ρ g z +C, при x=0, z=0, P=P₀  , C= P₀,  P=P₀ –ρ (а x+ gz), при dP=0, а dx= - g dz, dz= - а/g dx

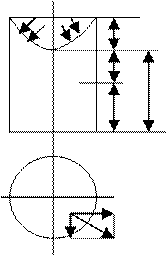
3) относительный покой ж-ти в сосуде, вращающемся с постоянной ω вокруг вертикальной оси

 

                                                   Н

                                                   z-z₀        z₀

                           M    

                                                   z

            r

                                          ω²x

                           ω²y           ω²r

 -dP+ ρ(I_x dx+ I_y dy+ I_z dz)=0, I_x= ω²x, I_y= ω²y, I_z= -g  -dP+ ρ(ω²x dx+ ω²y dy-g dz)=0, P= ρ(ω²x²/2+ ω²y²/2-g z)+C, при z=z₀, x=0, y=0, P=P₀, C= P₀+ ρ g z₀, P=P₀+ ρ(ω²r²/2+ g(z-z₀))

dP=0, ω²x dx+ ω²y dy-g dz=0, dz= ω²/g(x dx+y dy)+C, при z=z₀, x=0, y=0, C=z₀, z=z₀+ ω²r²/2g

если рассматривать свободную поверхность r=R, H=ω²R²/2g , ω=1/2√2gH, сосуд с жидкостью в данном случае м/б использован как жидкостной тахометр n=ω/2π

Давление абсолютное, избыточное и вакуумметрическое

Р_изб=Р_аб-Р_атм, избыточное - насколько абсолютное давление меньше атмосферного

Р_вак=Р_атм-Р_абс, вакуумметрическое – насколько абсолютное давление меньше атмосферного

Для измерения избыточного и вакуумметрического давления применяются жидкостные, механические и пьезоэлектрические приборы

Жидкостные: пьезометр

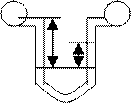
Дифференциальный манометр

  

                          Р₁                                       Р₂

                                    ρ₁

                                             х               b

                                               ∆h   

                                а

                                                ρ₂

P₁-P₂=? P_a=P_b , P_a= P₁+ ρ₁gx , P_b= P₂- ρ₁g(x-∆h) + ρ₂ g ∆h , P₁-P₂= g ∆h(ρ₂- ρ₁)

Батарейный жидкостной манометр

Механический манометр (вакуумметр)

Силы давления ж-ти на плоские стенки

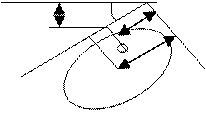
Рассмотрим силу давления ж-ти на плоскую стенку с одной стороны стенки

 

                   h                      α

                                                  y

                                        y_цт                               х

                                                      dS    

                                      S

dS- элементарная площадка площадь dS мала , давление во всех точках = , сила давления будет определяться: h= y sin α ,dФ = P dS= (P₀+ρ g h)dS ,Ф= P₀S= ρgsinαy_цтS

∫y dS =y_цт S – статический момент площади относительно оси х

Сила давления ж-ти на плоскую стенку = произведению давления в центре тяжести смоченной поверхности на площадь этой смоченной поверхности. Ф=Ф₁+Ф₂=Р₀ S+ ρ g h_цт S= сила внешнего давления + сила весового давления

Определение точки приложения силы весового давления

1

гидростатический парадокс

Ф₂= ρ g Н S , Н- высота ж-ти в сосуде

В случае, когда стенка расположена горизонтально α=0, т.е. представляет собой не боковую стенку, а дно сосуда суммарное давление определяется по тем же формулам. Давление на дно не зависит от формы и объёма сосуда, а только от площади дна и высоты столба ж-ти в сосуде, поэтому для сосудов разной формы заполненных одной ж-тью до одного уровня Н и имеющих одинаковую площадь дна сила полного давления на дно будет одинакова - гидростатический парадокс

Сила давления ж-ти на криволинейную стенку

Будем рассматривать симметричные криволинейные стенки имеющие общий центр кривизны, тогда все элементарные силы давления можно привести к одной равнодействующей. Пространственную силу давления можно разложить на 3 составляющие. т.к. горизонтальные составляющие определяются одинаково во всех направлениях то будем рассматривать 2 составляющие Ф_x и Ф_z

2

горизонтальная составляющая силы давления = произведению давления в центре тяжести вертикальной стенки на площадь проекции этой вертикальной стенки

Ф_z=ρg cosα ∫z dS Ф_z=ρ g cosα z_цт= ρ g V_{тела давления}

телом давления н-ся объём ограниченный криволинейной стенкой, свободной поверхностью или изометрической плоскостью и прямыми проектирующими криволинейную стенку на изометрическую плоскость. Тело давления действительное «+», мнимое «-».