Задача 1.8. Давление на поверхности воды в резервуаре измеряется ртутным U – образным манометром.
Как изменится показание h манометра, если его переместить вниз на а мм при неизменном давлении на поверхности воды и практически неизменном ее уровне?
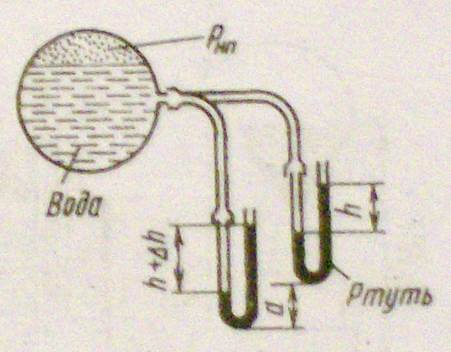
Решение.
Применим закон равновесия несжимаемой жидкости, из которого следует, что в жидкости плотностью ρрт = 13,546∙103 кг/м3 на границе раздела сред давление в трубках манометра одинаково. В правой трубке оно создается атмосферным давлением рат и весовым давлением столба ртути:
![]()
В левой трубке оно создано давлением рнп и весовым давлением столба воды:
![]()
Отсюда имеем:
![]()
![]()
При перемещении манометра вниз на а давление на границе раздела сред будет следующим:
![]()
![]()
Отсюда:
![]()
![]()
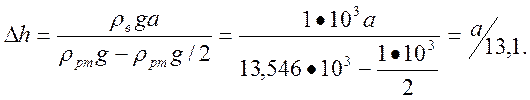
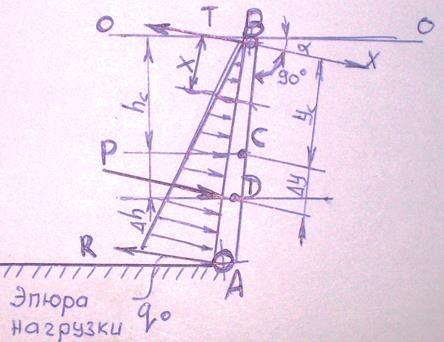
Задача 2.8. Клапанный затвор, имеющий плоскую поверхность размером L×B = 2,5×10 м, создает подпор воды Н=2,3 м.
Определить:
1) суммарную силу натяжения тросов Т, удерживающих затвор в заданном положении (без учета момента трения в опоре);
2) наибольший изгибающий момент М на затворе;
3) силу R, воспринимаемую цапфами опоры.
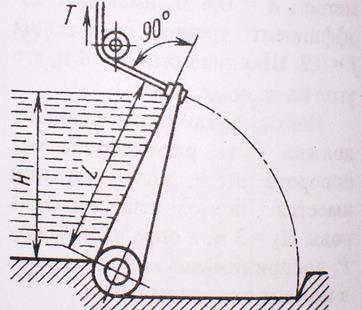
Решение.
Результирующая Р сил давления, воспринимаемая затвором и нормальная к ней:
![]()
где рСи – избыточное давление в центре тяжести площади F; hC – расстояние по вертикали от центра тяжести площади F до пьезометрической плоскости О – О (совпадает со свободной поверхностью воды).
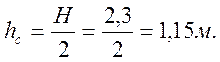
Площадь затвора:
![]()
![]()
Центр тяжести затвора уС:
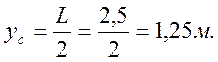
Центр давления силы Р:
![]()
Смещение центра давления:
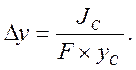
Для прямоугольника момент инерции:
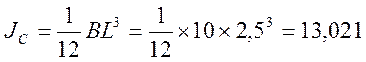
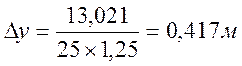
![]()
Определим силы Т и R.
Уравнения моментов будут иметь вид:
![]() ;
; ![]() ;
; 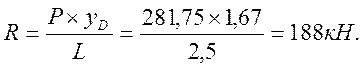
![]() ;
; ![]() ;
; 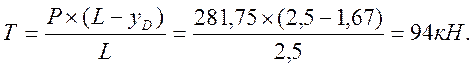
Для расчета наибольшего изгибающего момента затвора введем понятие наибольшей интенсивности нагрузки q0. Она равна наибольшему давлению:
![]()
Для построения эпюр возьмем сечение на расстоянии х от правого конца затвора. Ордината нагрузки в этом сечении q(x) определяется из подобия треугольников:
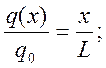
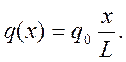
Для вычисления Q и M будем рассматривать правую часть затвора, так как на нее действуют сосредоточенная сила Т и треугольная нагрузка, в то время как на левую часть сила R и трапецеидальная нагрузка, что даст более сложные вычисления.
Поперечная сила Q будет равна сумме проекций на
вертикаль реакции Т и заштрихованной нагрузки 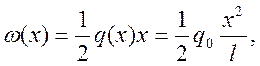 т.е.
т.е.
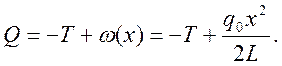
Через нуль поперечная сила переходит при х0, определяющемся из уравнения:
![]()
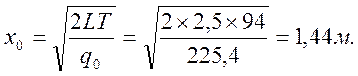
В этой точке достигает
максимума изгибающий момент. Опять рассмотрим правую отсеченную часть затвора
для расчета изгибающих моментов в затворе. Момент относительно точки О
равнодействующей заштрихованной треугольной нагрузки равен ее грузовой площади,
умноженной на плечо ![]() (место приложения
равнодействующей силы):
(место приложения
равнодействующей силы):
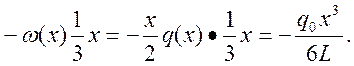
Изгибающий момент в проведенном сечении равен:
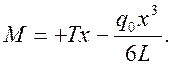
Это выражение для М пригодно на всем протяжении затвора. Наибольшее значение изгибающий момент получит в сечении, где Q=0, т.е. при х=х0=1,44 м:
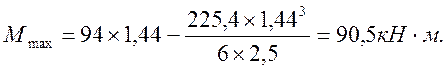
При практических подсчетах для балки, загруженной треугольной нагрузкой, всегда можно вместо Мmax вводить в вычисления момент посредине пролета. Ошибка не превышает 2,6 %.
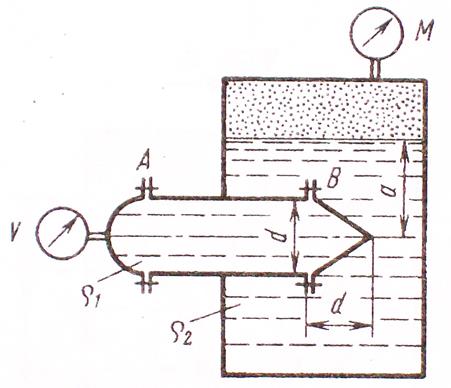
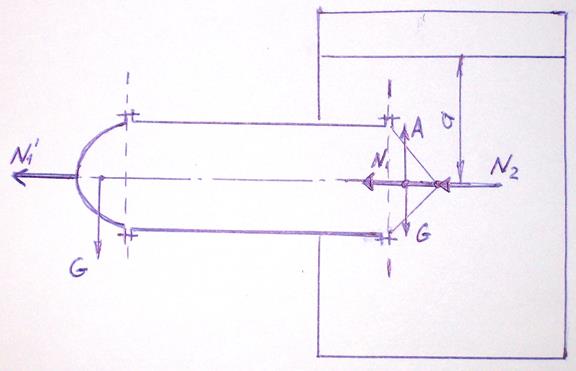
Задача 3.8. Горизонтальный цилиндрический сосуд диаметром d=0,8м с полусферической и конической тонкостенными крышками заполнен жидкостью плотностью ρ1. Правая половина цилиндра (с конической крышкой) вставлена в замкнутый резервуар и находится под уровнем другой жидкости (плотностью ρ2) на глубине а=2м.
Определить горизонтальные РГ и вертикальные РВ составляющие сил давления жидкости на полусферическую и коническую крышки А и В, если вакуумметра V=10 кПа, показание манометра М = 30 кПа и ρ1 = ρ2 =1000 кг/м3.
Показать в виде векторов горизонтальные и вертикальные составляющие сил давления жидкости на полусферу и конус. Как изменятся силы при ρ1 = 0,8 ρ2 = 800 кг/м3.
Решение
1. Коническая крышка
Рассчитаем горизонтальную составляющую. Для этого воспользуемся гидравлическим парадоксом Галилея, который гласит что давление на стенки сосуда определяется глубиной жидкости в сосуде независимо от формы стенок сосуда. В таком случае нам достаточно рассчитать давление жидкостей на вертикальную проекцию крышки по отдельности и затем сложить их векторно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.