Рассмотрим давление жидкости ρ1. Вакуумметр расположен на оси крышки. Поэтому рГ1 = V = 104 Па. Действие этой силы направлено внутрь сосуда (вакуум):
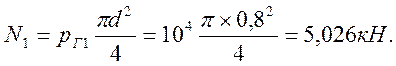
Рассмотрим давление жидкости ρ2. Жидкость воздействует на крышку с силой N2 направленной внутрь цилиндра:
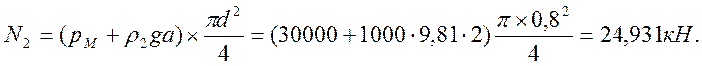
Их равнодействующая:
Как видно из уравнений, при изменении плотности ρ1 значение составляющих сил не изменится. А значит и их равнодействующая не изменится.
Рассмотрим вертикальную составляющую. Со стороны жидкости ρ1 на крышку воздействует сила веса жидкости, ограниченной конической крышкой:
Со стороны жидкости ρ2 на крышку действует архимедова сила:
Их равнодействующая:
При ρ1= ρ2
=0
При ρ1= 0,8 ρ2
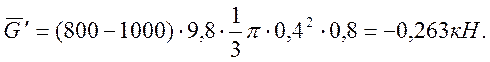
2. Полусферическая крышка
Рассуждая аналогичным образом, получаем что на крышку в горизонтальном направлении действует лишь сила N1 = 5,026 кН. Направлена она внутрь цилиндра. При изменении плотности горизонтальная составляющая не изменится.
Вертикальная составляющая состоит лишь из веса жидкости, ограниченной полусферой:
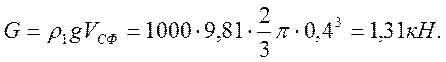
При изменении плотности:
G=0,8∙1,31=1,05 кН.
Задача 4.8.Закрытый цилиндрический сосуд диаметром D=0,6 м, имеющий полусферическое дно, наполнен до уровня Н=0,8 м водой и движется прямолинейно под углом α=30 ̊ к горизонту с постоянным ускорением а=2g.
Определить вертикальную РВ и горизонтальную РГ силы давления на дно, если избыточное давление газа над поверхностью воды в сосуде рИ=20 кПа и поверхность воды не касается крышки.
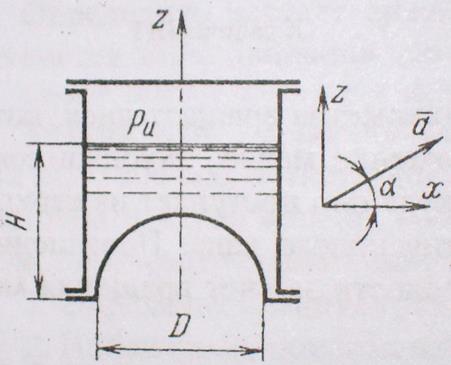
Решение.
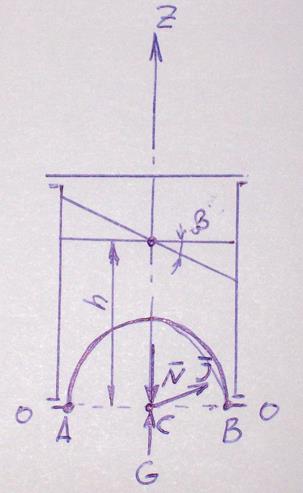
При движении с ускорением под углом к горизонту поверхность воды наклонится к горизонту с углом β, вычисляемый по формуле:
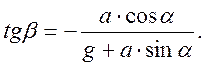
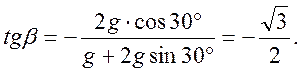
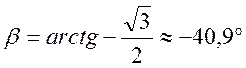
Найдем силу давления Р воды на дно из условий относительного равновесия жидкости объемом V, заключенным между криволинейной стенкой и плоским сечением, проведенным через граничный контур стенки:
где 
- сила давления на плоское сечение АСВ,
проведенное через граничный контур дна; 
-
вес объема V воды; 
-
сила инерции жидкости, заключенной в объеме V.
Так как дно выгнуто вовнутрь, то G и Jбудут вычитаться (направлены в противоположную сторону).
Сила давления на плоское сечение:
Давление в точках,
находящихся на глубине h
под поверхностью с давлением 
, выражается
соотношением:
Из условия неизменности
объема воды в сосуде следует, что свободная поверхность должна вокруг оси О,
расположенной на середине длины сосуда и нормальной к плоскости движения. Центр
тяжести круга совпадает с центром окружности. Таким образом 
. Отсюда:
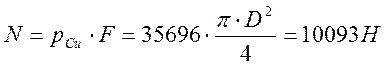
Вес воды в полусфере:
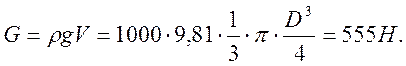
Сила инерции воды в полусфере:
Найдем проекции этих сил на вертикальную ось:
Проекции этих же сил на горизонтальную ось:
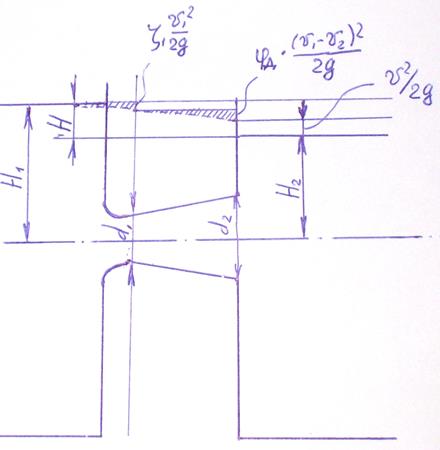
Задача 6.8. Вода перетекает из сосуда А в сосуд В через плавно сходящийся насадок диаметром выходного сечения d1 = 100 мм (коэффициент сопротивления ζ = 0,008) и приставленный к нему с небольшим зазором расходящийся конический насадок выходным диаметром d2 = 150 мм (коэффициент потерь φд = 0,3)
При заданном уровне Н1 = 2,5 м определить уровень Н2, при котором протекающая по насадкам вода не будет выливаться через зазор, а атмосферный воздух не будет засасываться внутрь насадков.
Построить график напоров.
Указание. В сечении потока, соответствующем зазору между насадками, давление должно равняться атмосферному.
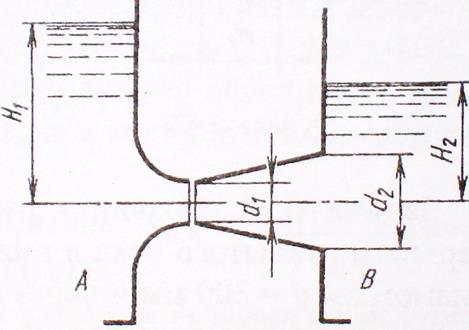
Решение.
При расчетах будем рассматривать данную комбинацию насадков как один насадок. Для рассматриваемого насадка (предполагая квадратичную зону истечения и пренебрегая неравномерностью распределения скоростей по сечению) имеем:
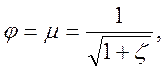
где ζ – коэффициент сопротивления насадка.
Пользуясь приемом суммирования потерь, получаем:
,
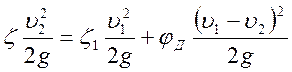где υ1 и υ2 – скорости во входном и выходном сечениях диффузора.
Так как по уравнению расхода:
то коэффициент сопротивления:
где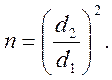 
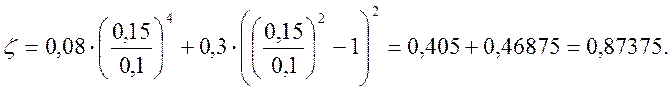
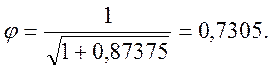
Скорость истечения:
При истечении под уровень, как в нашем случае, напор истечения Н представляет разность гидростатических напоров:
Для определения уровня Н2 рассмотрим истечение воды в атмосферу через плавно сходящийся насадок с давлением в сечении 1 – 1 р1 = рат .
Составим уравнение Бернулли для участка 0 – 1:
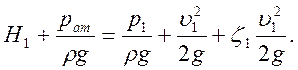
Подставляя зависимости в формулу, получим:
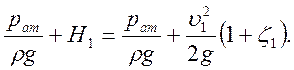
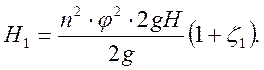
Отсюда:
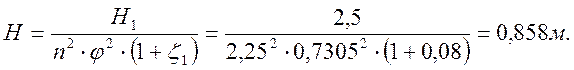
Построение графиков напоров дано на рисунке.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.