Исследование режимов течения жидкости: Методические указания к выполнению лабораторной работы, страница 6

 

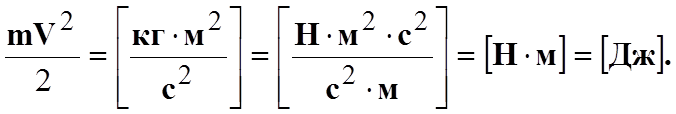
Таким образом, для элементарной струйки идеальной жидкости удельная энергия жидкости постоянная.

Графическая иллюстрация уравнения Бернулли для элементарной струйки идеальной жидкости представлена на рис.3.

На рис.3 необходимо обратить внимание на то, что линия полного напора располагается горизонтально, т. е. это постоянная величина.

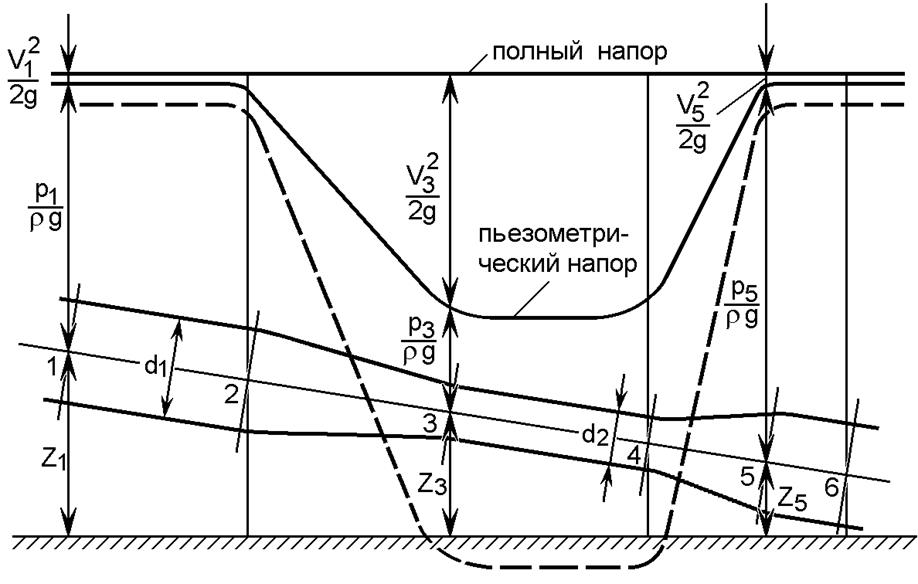
Рис.3. Изменение пьезометрического и скоростного напора вдоль струйки идеальной жидкости

Б. Уравнения Бернулли для потока реальной жидкости

При переходе от элементарной струйки идеальной жидкости к потоку реальной (вязкой) жидкости, имеющему конечные размеры и ограниченному стенками, необходимо учесть неравномерность распределения скоростей по сечению потока, а также потери энергии (напора). То и другое является следствием вязкости жидкости.

Неравномерность распределения скоростей по сечению потока учитывается коэффициентом Кориолиса:

a = 2 - для ламинарного режима течения жидкости;

a = 1,05 - 1,13 - для турбулентного режима течения жидкости.

Потери напора на участке между рассматриваемыми сечениями потока определяются в зависимости от характера сопротивлений на этом участке и подробнее будут рассмотрены в соответствующих лабораторных работах.

Исходя из описанных условий уравнение Бернулли для потока реальной жидкости имеет вид

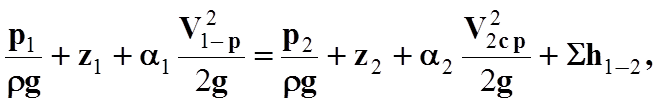                            (3)

где a₁ и a₂ - коэффициенты Кориолиса для соответствующих сечений;

       - суммарная потеря полного напора на участке между рассматриваемыми сечениями.

Выражение (3) графически иллюстрируется на рис.4.

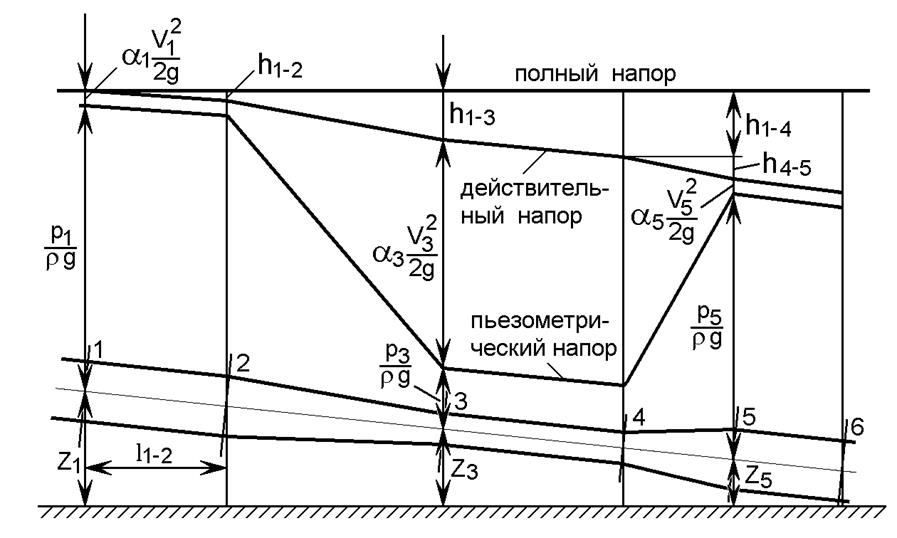
Рис.4. Изменение пьезометрического и полного напора

вдоль потока реальной жидкости

Из рисунка видно, что действительный напор в каждом последующем  сечении уменьшается на величину потерь hi, затрачиваемых на трение жидкости.

4.2. Экспериментальная часть

А. Лабораторная установка

Лабораторная установка, позволяющая изучить изменение пьезометрического и скоростного напоров при течении воды по трубопроводу переменного сечения, состоит (рис. 5) из напорного бака  1, трубопровода 2, на каждом характерном участке которого установлены попарно пьезометрические трубки 3 и гидрометрические трубки Пито 4, и мерного бака 6. Регулирование расхода жидкости по трубопроводу 2 осуществляется вентилями 5. Трубопровод 2 установлен горизонтально и имеет четыре участка с различными внутренними диаметрами (d₁, d₂ ,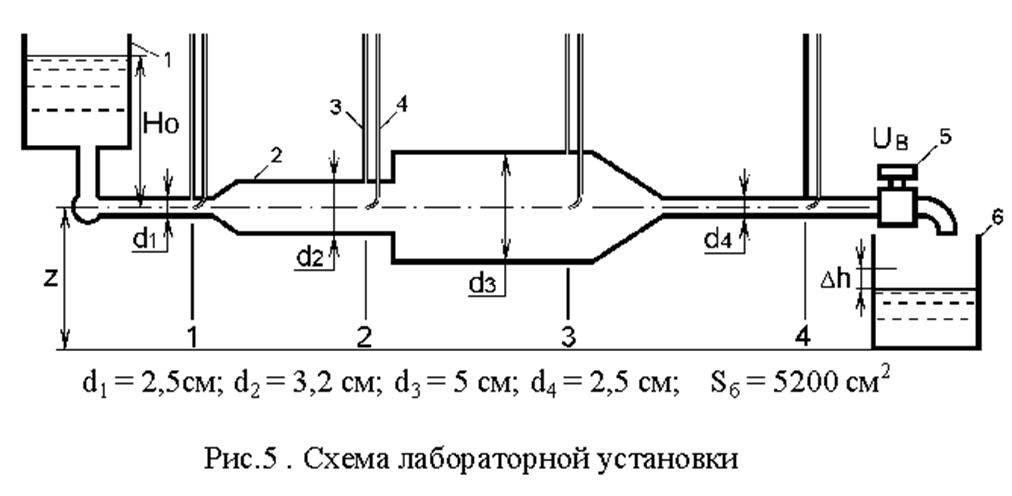
d₃ и d₄ ), соединенными различными переходами.

Б. Порядок проведения опытов

Эксперименты проводят при турбулентном режиме движения жидкости.

Для проведения опытов напорный бак заполняется водой до уровня Н_о при закрытом вентиле 5. Для этого в ячейку D22 ввести величину Н_о, заданную преподавателем. Затем, открывая вентиль 5, провести опыты. Для этого ввести в ячейку W37 значение параметра регулирования вентиля (величины открытия) Uв  в пределах от 0 до 1 по заданию преподавателя. Проводится два опыта.

Для каждого опыта определить величину приращения уровня воды в мерном баке Dh, взяв его значение из ячейки U48, и снять последовательно показания пьезометров и трубок Пито по выделенным сечениям. Все результаты занести в таблицу.

В. Обработка экспериментальных данных

1. Определить секундный расход воды

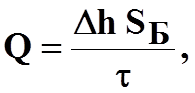
где S_Б - площадь мерного бака (S_Б = 5200 см²);

      Dh - приращение уровня в мерном баке, см;

        t - время опыта, с (t =30 с).

2. Определить среднюю скорость течения воды в каждом сечении трубопровода, см/с:

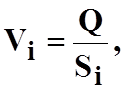
где 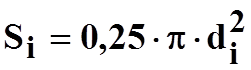 - площадь живого сечения трубопровода, см².

Здесь d_i - внутренний диаметр сечения трубы, см.

3. Определить скоростной напор в каждом сечении, см.

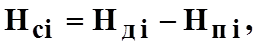
где 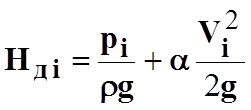 - показания трубки Пито в i сечении (действительный напор);

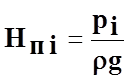      - показания пьезометрической трубки в i сечении (пьезометрический напор).

4. Определить среднюю скорость воды в сечениях по скоростному напору, см/с:

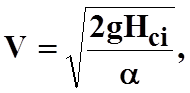
где a - коэффициент Кориолиса. Для турбулентного режима принять

 a = 1,1.

5. Определить потери напора по участкам трубы, см:

,

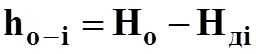где H_o - полный напор, см.