При небольшой скорости движения жидкости краска, попав в поток жидкости в виде тонкой струйки, продолжает на всем протяжении потока двигаться струйкой (рис.1,а). Это значит, что частицы испытуемой жидкости также движутся струйчато (слоисто). Это ламинарный режим.

Рис. 1. Режимы движения жидкости
При увеличении скорости движения жидкости окрашенная струйка приобретает волнистое очертание (переходная зона), а затем внезапно разрушается на отдельные частицы, которые далее двигаются по случайным неопределенно искривленным траекториям, окрашивая весь поток жидкости. Это турбулентный режим. При таком режиме часть энергии затрачивается на поперечное перемещение и перемешивание частиц жидкости, вследствие чего турбулентный режим требует больших удельных затрат на перемещение жидкости, чем ламинарный.
На основе эксперимента может быть построен график зависимости числа Рейнольдса от скорости потока жидкости (рис.2), на котором будут отмечены моменты перехода режимов движения жидкости один в другой и наоборот.
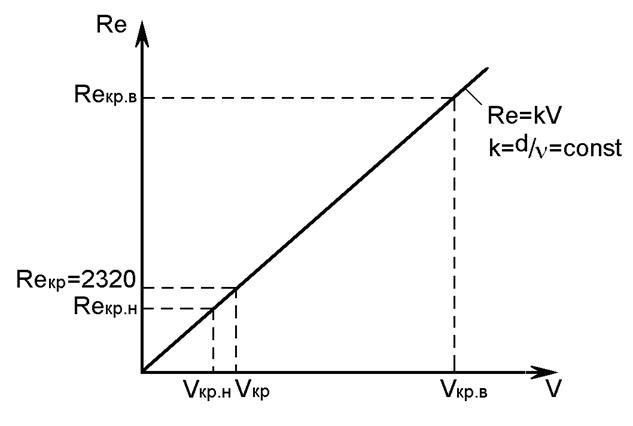
Рис.2. Зависимость числа Рейнольдса от скорости потока жидкости
Рейнольдс определил два критических числа - верхнее и нижнее. Верхнее критическое число Рейнольдса соответствует моменту перехода от ламинарного режима к турбулентному: Reкр.в=12000. Нижнее критическое число Рейнольдса соответствует моменту перехода от турбулентного режима к ламинарному: Reкр.н = 998. На участке между этими двумя критическими числами Рейнольдса возможно существование как ламинарного, так и турбулентного режима движения жидкости. Это зависит от условий входа жидкости в трубу, шероховатости стенок и других случайных факторов.
В практических расчетах число Рейнольдса используется при определении сопротивления трубопроводов. Обычно для жестких трубопроводов критическое число Рейнольдса принимают Reкр =2320.
При Rei < Reкр ламинарное движение является вполне устойчивым: всякого рода искусственная турбулизация потока и его возмущения (сотрясение трубы, введение в поток колеблющегося тела и др.) погашаются влиянием вязкости, и ламинарный режим течения жидкости снова восстанавливается. При Rei > Reкр наоборот, турбулентный режим устойчив, а ламинарный не устойчив.
Если живое сечение потока отличается от круглого или в трубопроводе имеется большое число близко расположенных местных сопротивлений, критическое число Рейнольдса может отличаться от приведенного выше значения. Так, например, для гибких шлангов в системе гидропривода Reкр =1600.
От режима движения жидкости зависят не только потери на преодоление сопротивления трубопровода, но и энергетические параметры потока. На рис.3 показаны эпюры скоростей в живом сечении потока жидкости в круглой трубе.
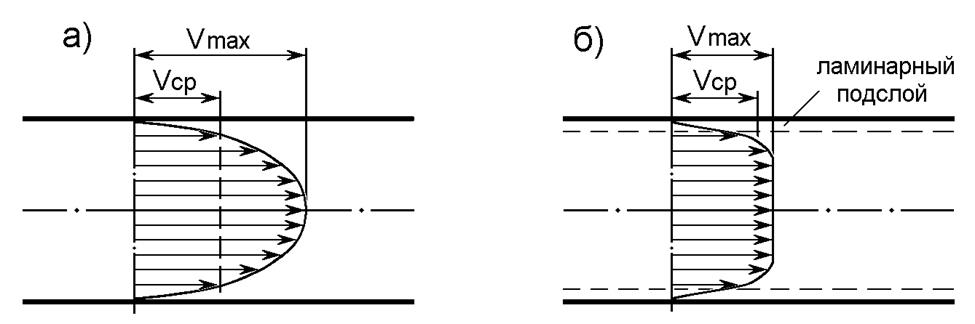
Рис.3. Эпюры скоростей при ламинарном (а) и турбулентном (б)
режимах движения жидкости
Эпюра скоростей в случае ламинарного режима в трубопроводе круглого сечения представляет собой параболоид вращения, ось которого совпадает с геометрической осью трубы. Сопротивление трубопровода в этом случае прямо пропорционально вязкости жидкости и обратно пропорционально числу Рейнольдса.
Расчетами можно доказать, что Vср = 0,5Vmax .
Эпюра скоростей турбулентного режима имеет ярко выраженное турбулизированное ядро потока с примерно одинаковыми средними скоростями. Лишь частицы жидкости, близко расположенные к стенке, испытывают от нее тормозящее действие сил трения и образуют так называемый ламинарный подслой. В этом случае сопротивление трубопровода в наибольшей степени определяется шероховатостью стенок трубы и имеет квадратичную зависимость от скорости жидкости и числа Рейнольдса. Средняя скорость потока Vср несколько меньше Vmax, а при абсолютно турбулентном режиме (что возможно только теоретически для идеальной жидкости) Vср = Vmax .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.