Метод конечных элементов для расчета конструкций (Специальная часть дипломного проекта)

СОДЕРЖАНИЕ:

2.1 Введение…………………………………………….2

2.2 Построение геометрической модели……………3

2.3 Анализ результатов…………………………….…9

2.4 Техническое решение……………………………..12

Обозначение остальных частей:

Технологическая часть                                       ДП.ТЧ.КМ130.03.00.000.

Автоматизация проектирования                      ДП.АП.КМ130.04.00.000. Экономическая часть                                          ДП.ЭЧ.КМ130.05.00.000.

Техника безопасности                                          ДП.ТБ.КМ130.06.00.000.

2. СПЕИАЛЬНАЯ ЧАСТЬ

2.1. Введение

 Создание современных металлических конструкций шахтных крепей, отвечающих требованиям эксплуатации, связано с повы­шением их технологичности и несущей способности. Металлокон­струкции шахтных крепей, как правило, работают в сложных гор­но-геологических условиях, подвергаясь при этом различным ви­дам нагрузок и деформаций.

Кроме того, на напряженно-деформированное состояние кон­струкций серьезно влияют остаточные сварочные напряжения, воз­никающие в процессе их изготовления и достигающие значений, со­измеримых с расчётными от внешних нагрузок.

Остаточные напряжения в сочетании с напряжениями от горно­го давления приводят к изменению расчетных схем металлокон­струкций крепей и отдельных элементов, к существенному (до 20 - 30 %) снижению их несущей способности. Вот почему применяе­мые в настоящее время расчеты на прочность не вполне соответ­ствуют действительным условиям работы конструкций и не могут гарантировать надежности их работы.

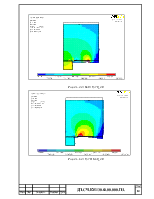
В данной части дипломного проекта изложены основные положения мето­дики для расчёта взаимодействия верхняка крепи с массивом горной породы и представлены эпюры напряжений, возникающих в массиве горной породы .Существующие методы расчета шахтных крепей пригодны лишь для ориентировочных расчетов, так как они базируются на применении общемашиностроительных методов расчета и не отражают влияния конструктивно-технологи­ческих факторов на несущую способность конструкций.

В практике мирового крепестроения все больше применяются современные научно обоснованные методы исследований и расче­тов. В связи с этим приведены основные положения метода конеч­ных элементов (МКЭ) для расчета несущих элементов крепей и результаты математического моделирования на ЭВМ напряженно-деформированного состояния (НДС) металлоконструкций.

Применение МКЭ для расчета конструкций крепей дало воз­можность учесть их пространственную многомерность, жесткость сопряженных элементов, реальные условия нагружения и прило­жения опорных реакций.

Метод конечных элементов (МКЭ) является мощным и надёжным средством исследования поведения конструкций в условиях разнообразных воздействий.

В настоящее время на рынке программного обеспечения имеется  большое количество комплексов МКЭ, в том числе ANSYS, NASTRAN, ABAQUS, COSMOS и др. Традиционно эти продукты относятся к категории CAE (Computer Aided Engineering) программного обеспечения, применяемого при проектировании конструкций. Эта категория программного обеспечения занимает прочное место в списке CAD/CAM/CAE/GIS/PDM, продуктами из которого  том или ином виде пользуется большинство инженеров во всём мире.

Метод конечных элементов ANSYS широко известен и пользуется популярностью среди инженеров – исследователей, занимающихся вопросами динамики и прочности. Средства МКЭ ANSYS позволяют проводить расчёты статического и динамического напряжённо-деформированного состояния конструкции (в том числе геометрически и физически нелинейных задач механики деформируемого твёрдого тела), форм и частот колебаний, анализа устойчивости конструкции, нелинейных переходных процессов и др.

                      2.2. Построение геометрической модели.

     Геометрическая модель представляет собой плоскую картину взаимодействия верхняка механизированной крепи с массивом горной породы в механизированной лаве шахты.

    Построение плоской геометрической модели производится в программе ANSYS в  натуральную величину (в метрах). По геометрическим размерам были созданы ключевые точки. Далее по ключевым точкам были созданы линейные объекты ,часть из которых была объединена в поверхности. Геометрическая модель состоит из пяти элементов:

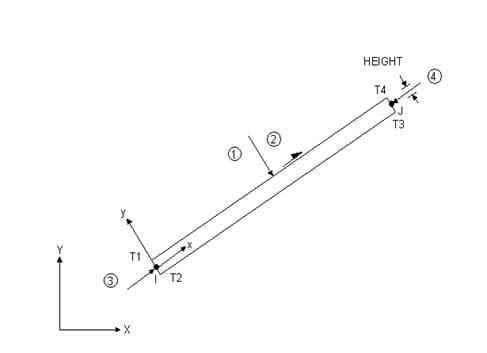
      1 Element – BEAM3 упругая балка ,которая эмитирует верхняк шарнирно соединенный с козырьком механизированной крепи.

Краткие сведения:   - 2 узла;

                                    -DOF: UX, UY, ROTY;

                                    -Форма: прямая.

     2 Element – PLANE42 прочностной твердотельный элемент эмитирует массив горной породы ,  который расположен непосредственно над верхняком крепи.

Краткие сведения:   - 4 узла; 2D;

                                    -DOF: UX, UY;

                                    -Форма: четырехугольник.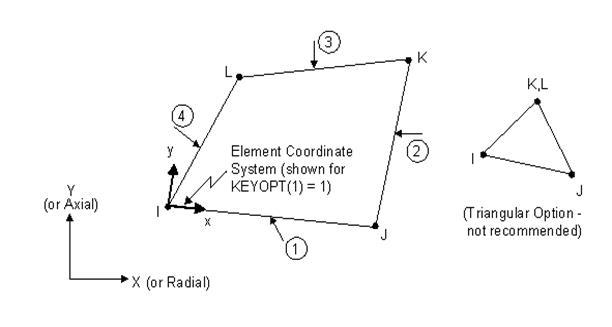

     3 Element – PLANE42  прочностной твердотельный элемент эмитирует массив угольного пласта.

Краткие сведения:   - 4 узла; 2D;

                                    -DOF: UX, UY;

                                    -Форма: четырехугольник.

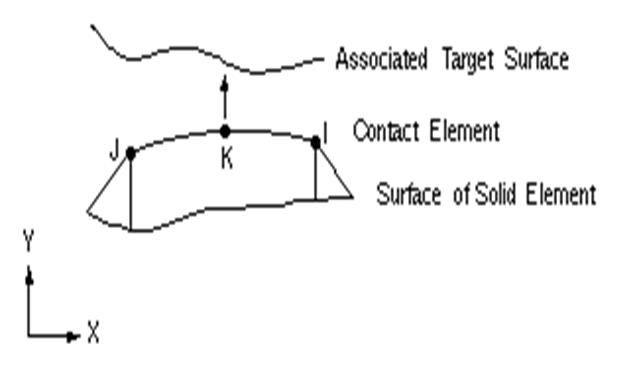
     4 Element – TARGE169 элемент контакта, который обеспечивает взаимодействие между породой и верхняком.

Краткие сведения:   - 1,2 или 3  узла; 2D;

                                    -DOF: UX, UY, ROTZ, TEMP;

                                    -Форма: прямая, дуга, парабола, окружность, точка.

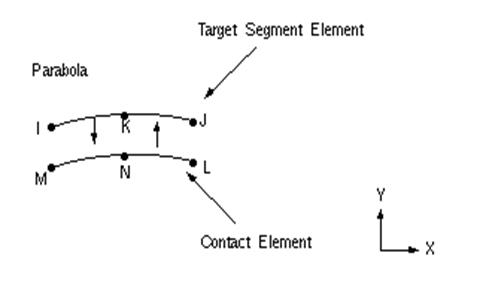
    5 Element – CONTA172 элемент контакта, который обеспечивает взаимодействие между породой и верхняком.

Краткие сведения:   - 3  узла; 2D;

                                    -DOF: UX, UY, TEMP;

                                    -Форма: парабола.

   Следующим этапом моделирования стало задание необходимых свойств материалов, которые сведены в таблицу 2.2.1