Страхование валютных рисков. Расчет валютного риска компании, страница 2

Изменение стоимости (прибыль или убыток) откладывается по оси ординат, а 30-дневный форвардный обменный курс – по оси абсцисс.

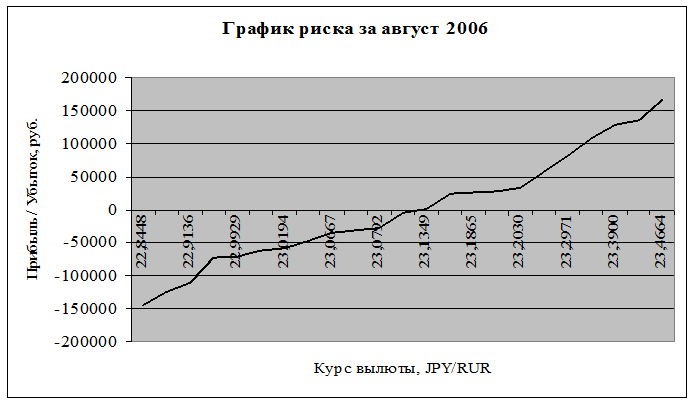
Однако график риска не несет полной информации о подверженности компании валютному риску, так как не отражает степень изменчивости курса. Для этого необходимо произвести соответствующие расчеты.

3.    Произведем расчет дисперсии, представленной в уравнении, с помощью, которой измеряется изменчивость курса, и среднеквадратического отклонения, которое вычисляется как квадратный корень из дисперсии:

σ² = ∑ (С_i – C_ср)² / (n – 1)

                                            Среднеквадратическое отклонение =σ²

где    σ² – дисперсия;

         С_i– курс валюты согласно варианту;

         C_ср – средний курс валюты согласно варианту;

         n – число наблюдений.

Расчеты занесем в таблицу.

Число наблюдений	Курс САD/RUR на август 2006	Величина прибыли,  руб.	(С - Сср)	(С - Сср)2
1	23,6735	11836750	-0,1924	0,0370
2	23,7138	11856900	-0,1521	0,0231
3	23,7173	11858650	-0,1486	0,0220
4	23,7196	11859800	-0,1463	0,0214
5	23,7624	11881200	-0,1035	0,0107
6	23,7674	11883700	-0,0985	0,0097
7	23,7695	11884750	-0,0964	0,0092
8	23,7816	11890800	-0,0843	0,0071
9	23,7956	11897800	-0,0703	0,0049
10	23,7989	11899450	-0,067	0,0044
11	23,8141	11907050	-0,0518	0,0026
12	23825	11912500	-0,0409	0,0016
13	23,8446	11922300	-0,0213	0,0004
14	23,8451	11922550	-0,0208	0,0004
15	23,8722	11936100	0,0063	0,00003
16	23,8832	11941600	0,0173	0,0002
17	23,922	11961000	0,0561	0,0031
18	23,9991	11999550	0,1332	0,0177
19	24,0856	12042800	0,2197	0,0482
20	24,1101	12055050	0,2442	0,0596
21	24,169	12084500	0,3031	0,0918
22	24,181	12090500	0,3151	0,0992
Итого		262585300	0,0216	0,4743

Дисперсия: σ² = 0,4743 / (22 – 1) = 0,0225

Среднеквадратическое отклонение: σ = 0,0225 = 0,15

4.    Используя свойства нормального распределения, построим доверительный интервал и вычислим вероятности того, что обменный курс выйдет за определенные границы.

Доверительный интервал – это множество значений, симметрично распределенных относительно ожи­даемой величины, на которое выпадает заданная вероятность. Эта вероятность называется уровнем доверия. Если задается 90%-ный доверительный интервал, то он начинается в точке «ожидаемая величина минус 1,64 среднеквадратического отклонения» и заканчи­вается в точке «ожидаемая величина плюс 1,64 среднеквадратического отклонения». Если задается 95%-ный интервал как интервал от точки «ожидаемая величина минус 1,96 среднеквадратического отклонения» до точки «ожидаемая величина плюс 1,96 среднеквадратического отклонения».

Полученные данные представим в виде таблицы.

Доверительный интервал	Уровень доверия	Ожидаемая величина	Среднеквадратическое отклонение	Начальная точка интервала	Конечная точка интервала
90%	1,64	23,1349	0,15	22,884	23,376
95%	1,96	23,1349	0,15	22,836	23,424

  5.  Построим график доверительного интервала. Для этого необходимо определить изменение прибыли соответственно каждой границе интервала. Риск изменения прибыли для компании можно определить, умножив размер позиции в иностранной валюте (сумма векселя) на среднеквадратическое изменения курса. Этот риск прибыли может быть преобразован в доверительный интервал (90% или 95%) с помощью свойств нормального распределения: