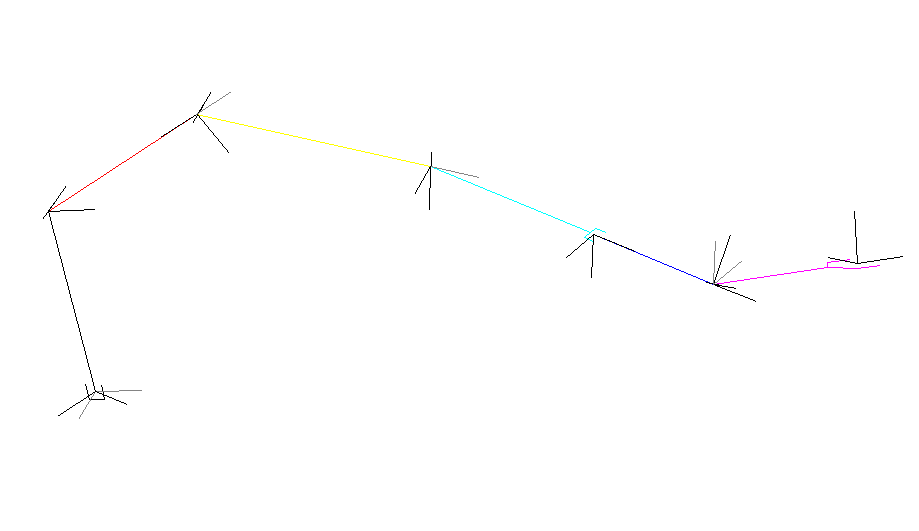
Рис.5 Кинематическая схема механизма.
Подготовка для расчёта обратной кинематической задачи методом Ньютона заключается в получении матрицы Якоби. В связи с большим объёмом расчётов определим лишь некоторые элементы данной матрицы (по координатам Х, Y, Z)
В общем случае матрица Якоби будет иметь вид :

Здесь : x,y,z-координаты вектора положения расчётной точки;
α,β,γ-углы ориентации рабочего органа;
q1..q6-обобщенные координаты.
Ниже приведены элементы матрицы Якоби В по координатам X, Y, Z.
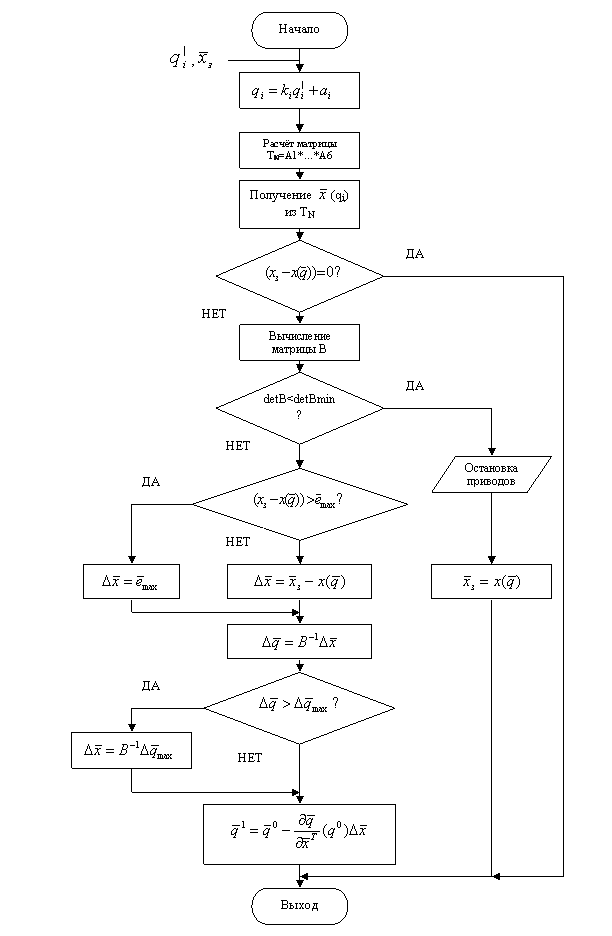
Алгоритм решения ПЗК и ОКЗ.
Расчёт влияния массы переносимого груза на инерцию 1-й оси механизма
Jгруза=R2m=(2.183)*(2.183)*80=381 кг*м2
Jдвигателя=0.000095 кг*м2
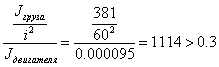 , таким образом требуется производить
учёт взаимного влияния координат исполнительного механизма в настройках
регуляторов приводов.
, таким образом требуется производить
учёт взаимного влияния координат исполнительного механизма в настройках
регуляторов приводов.
Программа решения прямой кинематической задачи
Программа решения прямой кинематической задачи написана на языке С++, текст программы представлен ниже :
#include <iostream.h>
#include <math.h>
void main ()
{
double a[6][4][4],t[6][4][4],s1,s2,s3,s4,s5,s6,q1,q2,q3,q4,q5,q6;
int k,i,j;
s1=1370;
s2=1000;
s3=700;
s4=300;
s5=0;
s6=183;
//Ввод углов
cout<<"\n Введите углы:\n";
cin>>q1>>q2>>q3>>q4>>q5>>q6;
q1=q1*((3.1415926535897932384626433832795)/180);
q2=q2*((3.1415926535897932384626433832795)/180);
q3=q3*((3.1415926535897932384626433832795)/180);
q4=q4*((3.1415926535897932384626433832795)/180);
q5=q5*((3.1415926535897932384626433832795)/180);
q6=q6*((3.1415926535897932384626433832795)/180);
//Определение матриц Аi
a[0][0][0]=-sin(q1); a[0][0][1]=0; a[0][0][2]=-cos(q1); a[0][0][3]=0;
a[0][1][0]=-cos(q1); a[0][1][1]=0; a[0][1][2]=sin(q1); a[0][1][3]=0;
a[0][2][0]=0; a[0][2][1]=1; a[0][2][2]=0; a[0][2][3]=s1;
a[0][3][0]=0; a[0][3][1]=0; a[0][3][2]=0; a[0][3][3]=1;
a[1][0][0]=sin(q2); a[1][0][1]=cos(q2); a[1][0][2]=0; a[1][0][3]=-s2*cos(q2);
a[1][1][0]=-cos(q2); a[1][1][1]=sin(q2); a[1][1][2]=0; a[1][1][3]=s2*sin(q2);
a[1][2][0]=0; a[1][2][1]=0; a[1][2][2]=1; a[1][2][3]=0;
a[1][3][0]=0; a[1][3][1]=0; a[1][3][2]=0; a[1][3][3]=1;
a[2][0][0]=-sin(q3); a[2][0][1]=0; a[2][0][2]=cos(q3); a[2][0][3]=-s3*sin(q3);
a[2][1][0]=cos(q3); a[2][1][1]=0; a[2][1][2]=sin(q3); a[2][1][3]=-s3*cos(q3);
a[2][2][0]=0; a[2][2][1]=1; a[2][2][2]=0; a[2][2][3]=0;
a[2][3][0]=0; a[2][3][1]=0; a[2][3][2]=0; a[2][3][3]=1;
a[3][0][0]=sin(q4); a[3][0][1]=0; a[3][0][2]=cos(q4); a[3][0][3]=s4*cos(q4);
a[3][1][0]=-cos(q4); a[3][1][1]=0; a[3][1][2]=sin(q4); a[3][1][3]=s4*sin(q4);
a[3][2][0]=0; a[3][2][1]=-1; a[3][2][2]=0; a[3][2][3]=0;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.