4.а) Расчёт 
:
если 
> 0,999… или < – 0,999…, то следует положить:
= ± 0,999… (для формата двойной вещественной
точности число «девяток» равно тринадцати);
тогда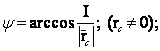 
если J < 0, то 
: = 2p - ;
далее j0=p + ; если j0 > 2p, то j0: = j0 - 2p.
4.б) Расчёт 
:
если 
>
0,999… или 
< – 0,999…, то следует положить:
= ± 0,999… (для формата двойной вещественной
точности число «девяток» равно тринадцати);
тогда 
если xK – xС < 0, то jK: = 2p - jK.
5. Формирование начального значения угла j и установка признака разрешения расчета дуги окружности:
j: = j0.
Далее приведён этап исполнения дуги окружности.
1. Признак разрешения расчета дуги установлен?
Нет, выход; да, перейти на п. 2 .
2. Анализ конца дуги:
½j - jк½ £ ½Dj½? да, j: = jк,
сбросить признак разрешения расчета дуги, на п. 4;
нет, j: = j + Dj, на п. 3.
3. Выполнение нормировки угла j:
j < 0? да? j: = j + 2p, на п. 4;
j > 2p? да, j: = j - 2p, на п. 4;
нет, на п. 4.
4. Расчет точки, лежащей на дуге:
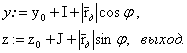
Рассмотрим далее алгоритмы разгона и торможения.
Для дуги :
-угол
в функции времени
-угловая
скорость
-угловые
ускорения разгона и торможения
Алгоритм разгона :
1. 
2. 
3. 
?
Да : окончить разгон, установить признак конца разгона, выход.
Нет : выход.
Алгоритм торможения :
1.
Определить остаток пути : 
2. Выполнено ли неравенство
Да : на п.3.
Нет : выход.
3.
;на п.4.
4.
?
Да : окончить торможение, установить признак конца торможения, выход.
Нет : выход.
Алгоритм расчета дуги ( с встроенными блоками разгона и торможения )
Нет : выход.
Да : на п.2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.