Проектування цифрових пристроїв на типових ІС та на ВІС програмованої структури з використанням моделюючого пакету MAX+plus II, страница 5

Рисунок 2.2 – Карта Карно для вихідної функції

Зчитуємо з карти Карно функцію:

Побудуємо схему порогового елемента:

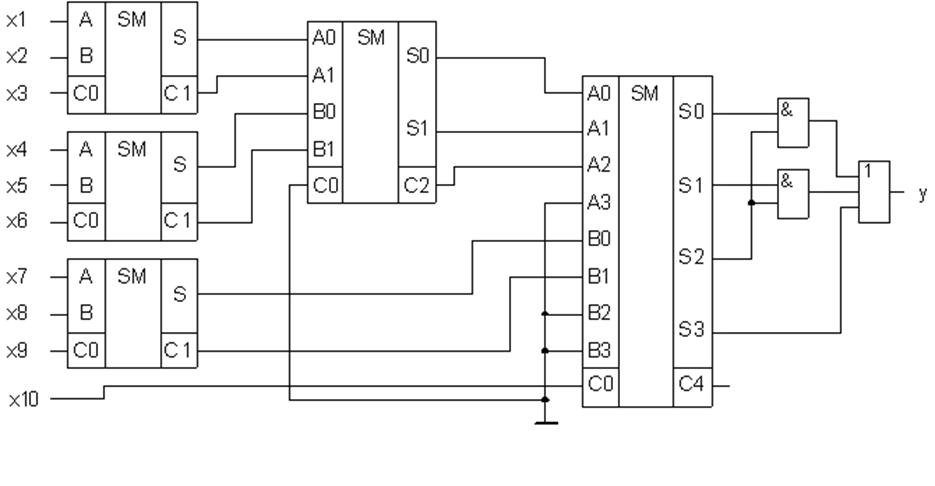
Рисунок 2.3 – Схема порогового елемента

2.3Автоматичне проектування пристрою на тому самому або вищому структурному рівні у текстовому редакторі MAX+plus II

Створюємо графічний файл зі схемою порогового елемента:

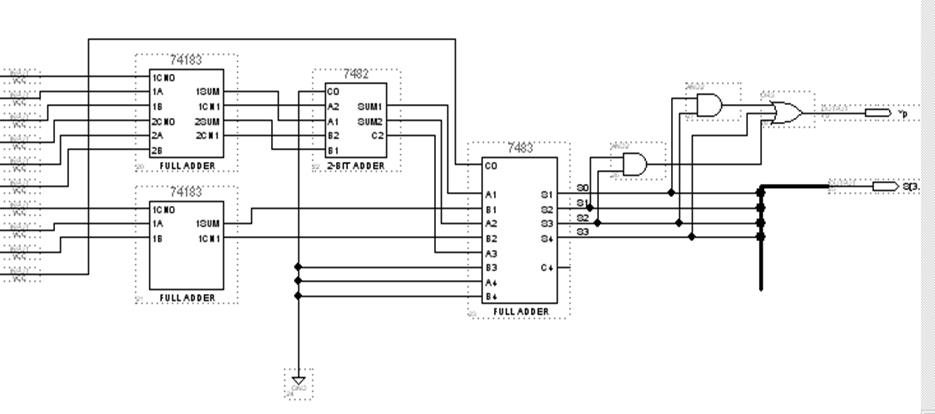
Рисунок 2.4 – Зображення порогового елемента в графічному редакторі

Компілюючи проект, отримаємо результати:

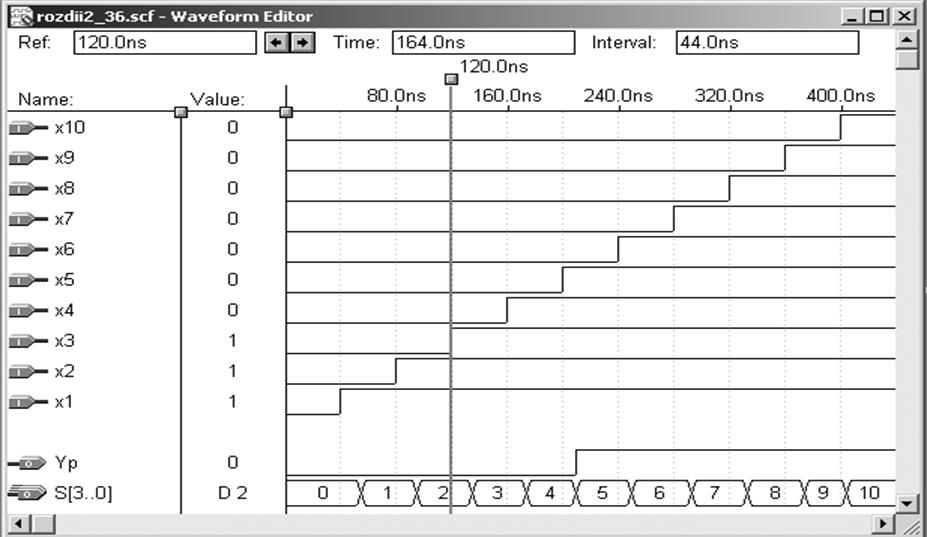
Рисунок 2.5 – Часові діаграми пристрою

З рис. 2.5 видно, що функція стає одиничною лише тоді, коли сума вхідних сигналів буде не менша 5. такі діаграми відповідають нормальній роботі пристрою.

2.3 Автоматичне проектування пристрою в текстовому редакторі MAX+Plus II

Опишемо мовою AHDL пороговий елемент :

TITLE "ПОРОГОВИЙ ЕЛЕМЕНТ НА SM і CMP";   

INCLUDE "rozdii2_36_cmp.inc"

FUNCTION 74183 (1cn0, 1b, 1a, 2cn0, 2a, 2b)

          RETURNS (1sum, 1cn1, 2sum, 2cn1);      

FUNCTION 7482 (a[2..1], b[2..1], c0)       

          RETURNS (sum[2..1], c2);

FUNCTION 7483 (a[4..1], b[4..1], c0)

          RETURNS (s[4..1], c4);

SUBDESIGN rozdii2_36_pe

(

          x1, x2, x3, x4, x5, x6, x7, x8, x9,x10 :  INPUT;

          Yp, S[3..0]                               :  OUTPUT;

)

VARIABLE

          sm1   : 74183;  sm2 : 7482;  sm3 : 7483;  cmp : rozdii2_36_cmp;

BEGIN   

          sm1.1cn0=x1; sm1.1a=x2; sm1.1b=x3;   

          sm1.2cn0=x4; sm1.2a=x5; sm1.2b=x6;

          sm1.2cn0=x4; sm1.2a=x5; sm1.2b=x6;

          sm2.a1=sm1.2sum; sm2.a2=sm1.2cn1; sm2.c0=x7;

          cmp.dataa[]=(sm2.c2, sm2.sum2, sm2.sum1);

          p=cmp.ageb; N[]=(sm2.c2, sm2.sum2, sm2.sum1);

END;

FUNCTION 7482 (a[2..1], b[2..1], c0)       

          RETURNS (sum[2..1], c2);

          p=cmp.ageb; N[]=(sm2.c2, sm2.sum2, sm2.sum1);

END;

Результати порівняння часових діаграм створених текстовим та графічним файлом наведені на рисунку 2.6.

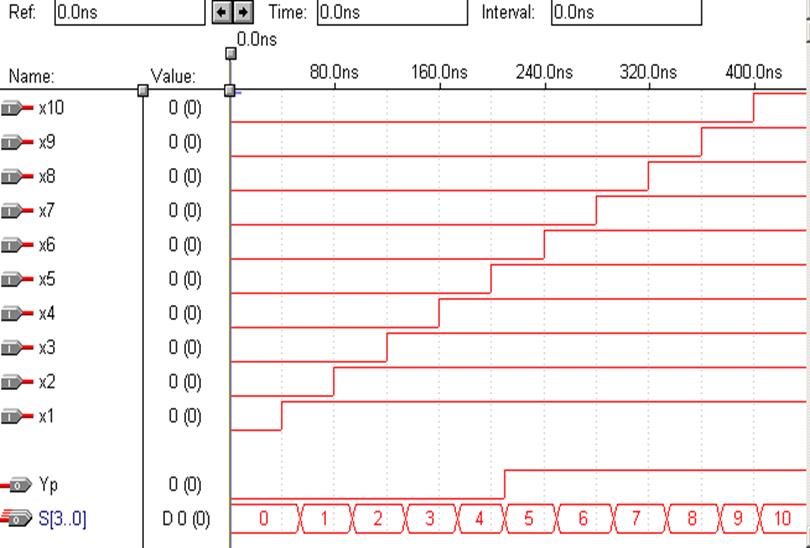
Рисунок 2.6 — Результати порівняння часових діаграм створених текстовим та графічним файлом

У даному розділі проводилось проектування пристрою на ЦКП, а саме: порогового елементу на суматорах з використанням логічних елементів. В ході проектування була наведена таблиця відповідності, діаграма термів, логічний вираз, по яким проводилась побудова порогового елементу. Виконавши автоматичне проектування пристрою на рівні макрофункцій у графічному та текстовому редакторах МАХ+рlus II, отримали часові діаграми, які виявилися ідентичними.  Тобто це свідчить, що проектування виконано вірно.

РОЗДЛ 3

3.1 Проектування ЦПП потрібного типу на основі заданої елементної бази. Задано тип регістра: регістр зсуву, кодова послідовність: 0001001. Спроектувати реверсивний генератор кодової послідовності.

1) Визначаємо модуль М=7, що дорівнює кількості символів у послідовності, та мінімальну кількість розрядів ГКП, яка становить n= 3, бо при  n= 2, як зазначено вище, деякі з вихідних кодів будуть однаковими.

Під час зсуву числа з послідовності символів на один крок у бік старших розрядів значення початкового коду N = Q₂Q₁Q₀ подвоюється (наприклад, 001 ® 010) і до молодшого розряду додається ще наступний символ x_N послідовності, тобто з надходженням чергового синхроімпульсу матимемо код  N⁺ = 2N + x_N. Але якщо є одиниця в старшому розряді, у наступному такті зсуву вона зникає, тому її вагу 2^n-1 перед подвоєнням треба відняти. Отже, наступний код можна визначити з виразу:

N⁺ = 2N + x_N, якщо N <  2^n-1; N⁺ = 2(N–  2^n-1 ) + x_N, якщо N ³ 2^n-1.

Так, при n= 3 робочий цикл буде слідуючим

N = Q₂Q₁Q₀ = (0001001) =0,1,2,1..

при n= 4

N = Q₂Q₁Q₀ = (0001001) =1,2,4,9,2...

 при n= 5

N = Q₂Q₁Q₀ = (0001001) =2,4,9,18,4...

при n= 6

N = Q₂Q₁Q₀ = (0001001) =4,9,18,36,8,17,34...

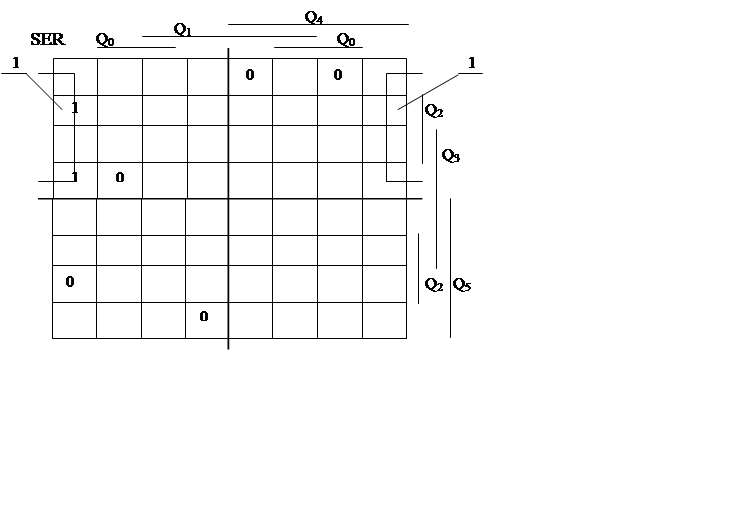
2) Мінімізуємо функцію збудження для входу послідовного введення SER (рис 3.1). Отже, для регістра на D-тригерах функція має вигляд:

 .

 

Рисунок 3.1 - діаграму термів (Вайча-Карно)