Проектування цифрових пристроїв на типових ІС та на ВІС програмованої структури з використанням моделюючого пакету MAX+plus II, страница 3

         

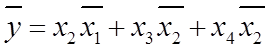
Рисунок 1.2 - Обчислення інверсного значення МДНФ

          МКНФ утворюється об’єднанням не одиниць, а нулів. Причому змінні, які входять до утворених об’єднань термів в протилежній до диз’юнктивної форми. Також тут якщо об’єднання входить до змінної, то змінна записується з інверсією, і навпаки якщо об’єднання не входить до змінної, то змінна записується без інверсії.

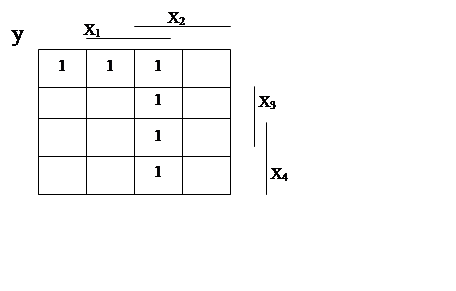
          Користуючись рисунком 1.3, знайшов МКНФ прямої форми:

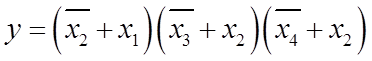
          Користуючись рисунком 1.4, знайшов МКНФ інверсної форми:

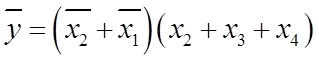
          Складність реалізації у булевому базисі досконалих форм на багато більша, ніж мінімальних форм. Безпосередньо це випливає з того, що до кожної групи досконалих форм входять усі чотири змінні . А у мінімальних формах, що найменше, виключається по одній змінній.

Рисунок 1.3 - Обчислення прямого значення МКНФ

 

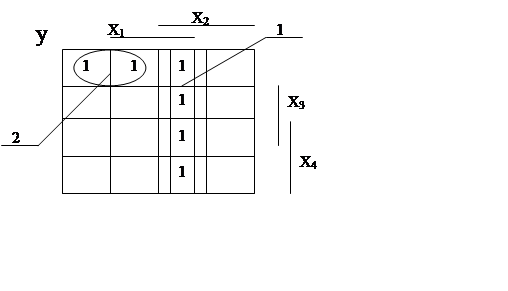Рисунок 1.4 - Обчислення інвесного значення МКНФ

1.3 Реалізація функції в базисах І-НЕ, АБО-НЕ та І-АБО-НЕ

Реалізація прямої функції в базисі І-НЕ зображена на рисунку 1.5. Приведемо пряму функцію МДНФ до відповідного базису:

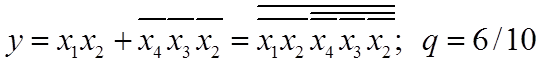
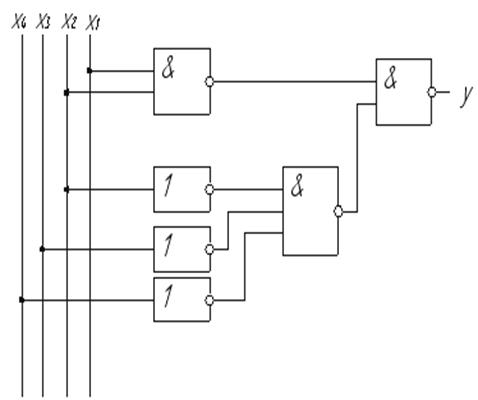
Рисунок 1.5 - Реалізація прямої функції в базисі І-НЕ

          Тут, і нижче елемент:

в базисі І-НЕ реалізується, як

Реалізація інверсної функції в базисі І-НЕ зображена на рисунку 1.6. Приведемо інверсну функцію МДНФ до відповідного базису:

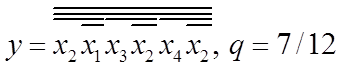
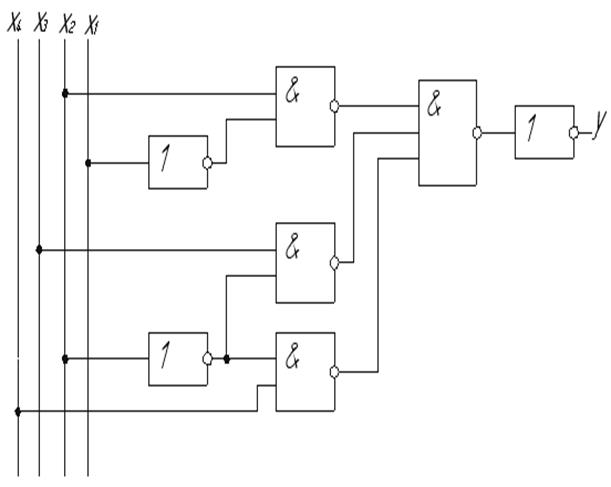
Рисунок 1.6 - Реалізація інверсної функції в базисі І-НЕ

Реалізація прямої функції в базисі АБО-НЕ зображена на рисунку 1.7 Приведемо пряму функцію МКНФ до відповідного базису:

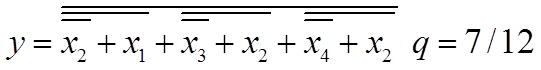
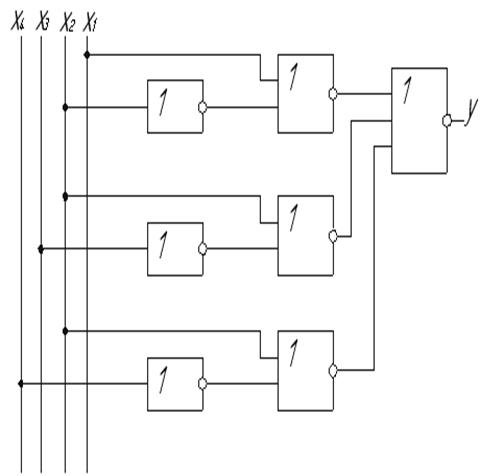
Рисунок 1.7 - Реалізація прямої функції в базисі АБО-НЕ

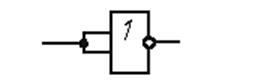
          Тут, і нижче елемент:

в базисі АБО-НЕ реалізується, як

Реалізація інверсної функції в базисі АБО-НЕ зображена на рисунку 1.8. Приведемо інверсну функцію МКНФ до відповідного базису:

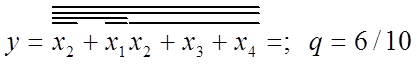
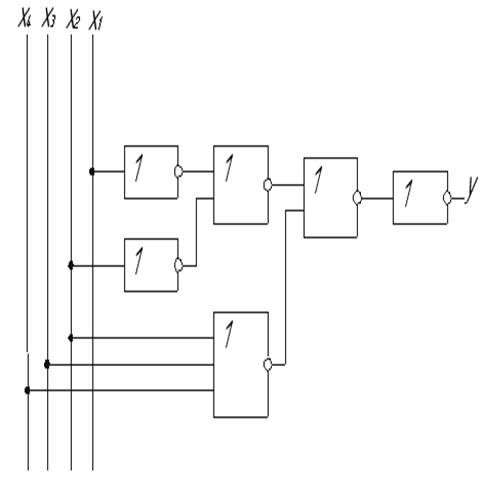
Рисунок 1.8 - Реалізація інверсної функції в базисі АБО-НЕ

Реалізація інверсної функції МКНФ в базисі І-АБО-НЕ зображена на рисунку1.9. Приведемо інверсну функцію МДНФ до відповідного базису:

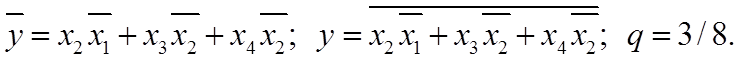
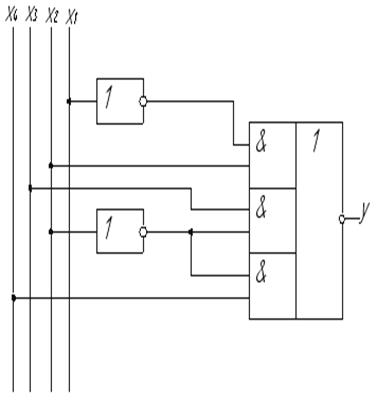
Рисунок2.9 - Реалізація функції в базисі І-АБО-НЕ

1.4 Мінімізація схеми в одному елементному базисі (І-НЕ чи АБО-НЕ), який потребує меншої кількості елементів

Знайдемо найбільш ефективну схему у базисі І-НЕ для прямого значення функції (рисунок 1.10) та приведемо її до потрібного базису, а також підрахуємо складність реалізації:

 

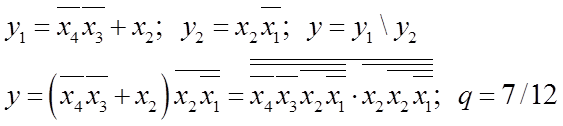
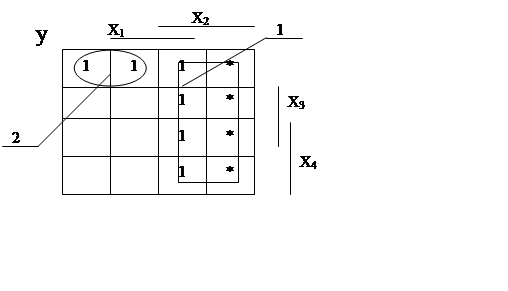Рисунок 1.10 - Мінімізація схеми в базисі І-НЕ

Реалізуємо схему отриманої функції (рисунок 1.11):

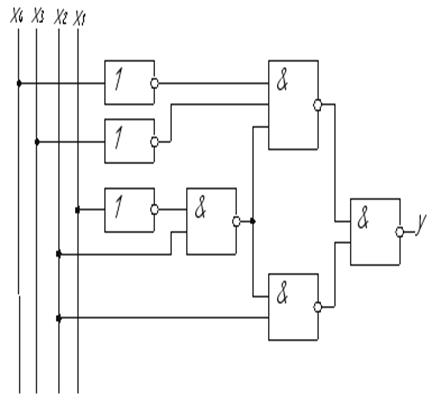
Рисунок 1.11 - Мінімізована схема в базисі І-НЕ

Знайдемо найбільш ефективну схему у базисі АБО-НЕ (рисунок 2.12) та приведемо її до потрібного базису, а також підрахуємо складність реалізації:

 

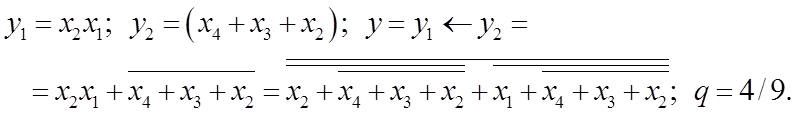
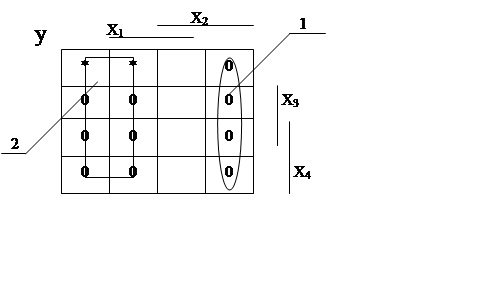Рисунок 1.12  - Мінімізація схеми в базисі І-НЕ

Реалізуємо схему отриманої функції (рисунок 1.13):

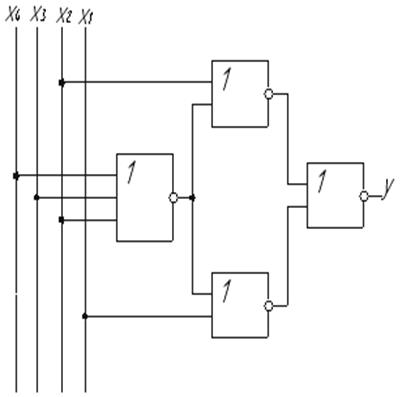
Рисунок 1.13 - Мінімізація схеми в базисі АБО-НЕ

          Порівнявши складності реалізації отриманих мінімальних форм, я вибрав схему рисунок 1.13 , так як вона вимагає найменшої кількості елементів та входів. Саме тому дана форма реалізації функції являється мінімальною формою.

2.5 Елементи технічного проектування мінімальної форми на інтегральних схемах вибраної серії (рисунок .14)

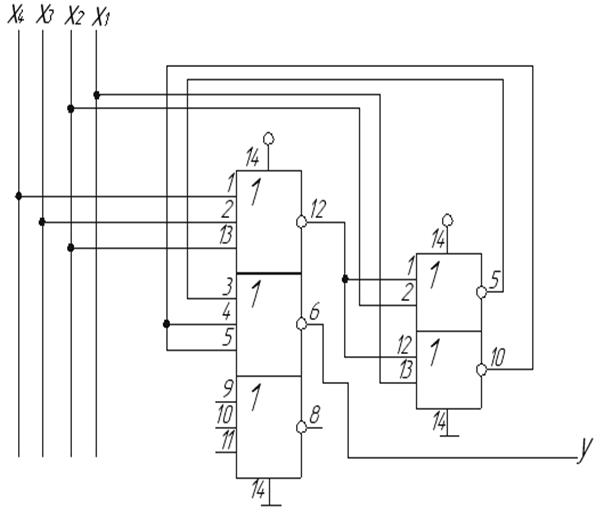
Рисунок  1.14 - Мінімальна форма на інтегральних схемах вибраної серії

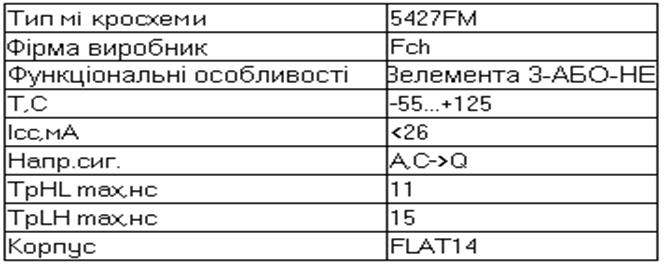
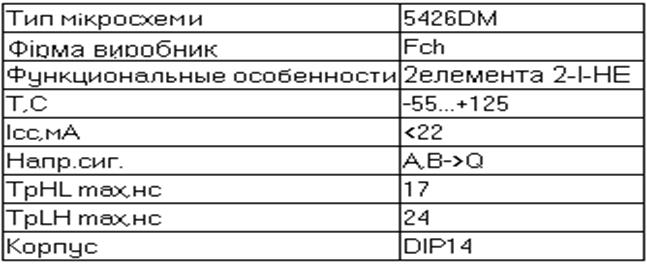
          Для реалізації отриманої мінімальноє форми я обрав дві інтегральні схеми 5427FM з трьома елементами АБО-НЕ та 5426DM  з двома елементами АБО-НЕ. Їх параметри приведені в табл 1.2 та 1.3 відповідно

Таблиця 1.2 — Параметри інтегральної схеми 5427FM

Таблиця 1.3 — Параметри інтегральної схеми 5426DM

2.6 Аналіз синтезованої мінімальної форми на ЕОМ

 Отриману синтезовану мінімальну форму я реалізував з допомогою пакету MAX+plus II.

          На рисунку 1.15 зображена схема реалізації функції, в базисі І-НЕ для прямого значеня функції.

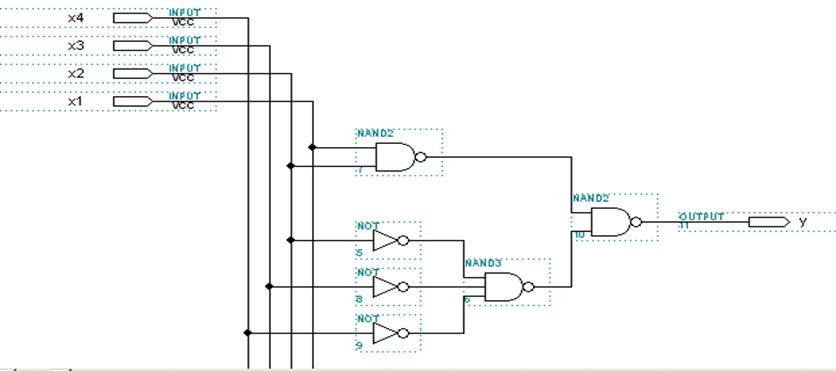
Рисунок 1.15 - Схема реалізації функції в базисі І-НЕ для прямого значення функції в програмі MAX+plus II

Результати моделювання даної форми наведені на рисунках 1.16-1.17