Проектування цифрових пристроїв на типових ІС та на ВІС програмованої структури з використанням моделюючого пакету MAX+plus II, страница 2

1.4 Мінімізація схеми в одному елементному базисі (І-НЕ чи АБО-НЕ), який потребує меншої кількості елементів. ………………………………………

1.5 Елементи технічного проектування мінімальної форми на інтегральних схемах вибраної серії ………………… ………………………………………

1.6 Аналіз синтезованої мінімальної форми на ЕОМ. ……………………

Розділ 2 …………………………………………………….…………………

2.1 Синтез порогового елементу (на SM, COMP) 5 З 10 (жорсткої стртуктури)

2.2 Автоматичне проектування пристрою на рівні макро або мегафункцій у графічному редакторі MAX+plus II. ……………………………….………

2.3Автоматичне проектування пристрою на тому самому або вищому структурному рівні у текстовому редакторі MAX+plus II ……………

Розділ 3 …………………………………………………….…………………

3.1 Проектування ЦПП потрібного типу на основі заданої елементної бази. 3.2 Аналіз функціонування пристрою, його самовідновність та повний перемикальний граф. Принципова схема ЦПП, часові діаграми перемикання з позначенням затримок. …………………………………………………….

3.3 Елементи технічного проектування. …………………………………

3.4 Аналіз спроектованого пристрою на ЕОМ………………….………………

Висновок…………………………………………………………………………

Список використаної літератури………………………………………………

СПИСОК СКОРОЧЕНЬ

ДДНФ – досконала диз’юнктивна нормальна форма

ДКНФ – досконала кон’юнктивна нормальна форма

МДНФ – мінімальна диз’юнктивна нормальна форма

МКНФ – мінімальна кон’юнктивна нормальна форма

ЦПП – цифровий послідовнісний пристрій

РОЗДІЛ 1

2.1 Мінімізація логічної функції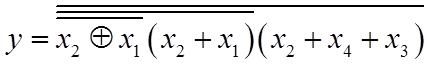

Побудуємо таблицю відповідностей та наведемо вирази для логічної функції y в досконалих формах (ДДНФ, ДКНФ).

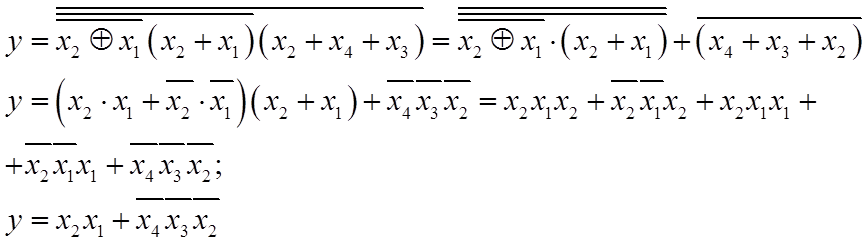
          Побудуємо таблицю відповідностей за отриманою ДДНФ. Тут комбінація розрядів двійкового числа одного з доданків (наприклад, 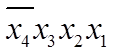 - це число 7, бо ) буде відповідати конкретному десятковому числу у таблиці відповідностей, при чому значення функції y для цього числа рівне одиниці (таблиця 1.1)

Таблиця 1.1- Таблиця істинності заданої функції

i	X4	X3	X2	X1	y
0	0	0	0	0	1
1	0	0	0	1	1
2	0	0	1	0	0
3	0	0	1	1	1
4	0	1	0	0	0
5	0	1	0	1	0
6	0	1	1	0	0
7	0	1	1	1	1
8	1	0	0	0	0
9	1	0	0	1	0
10	1	0	1	0	0
11	1	0	1	1	1
12	1	1	0	0	0
13	1	1	0	1	0
14	1	1	1	0	0
15	1	1	1	1	1

          Запишемо ДДНФ та ДКНФ для прямих та інверсних значень функції y :

ДДНФ:

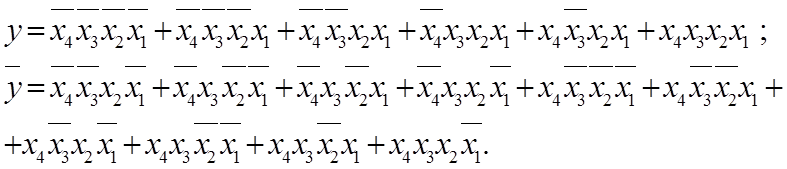
ДКНФ:

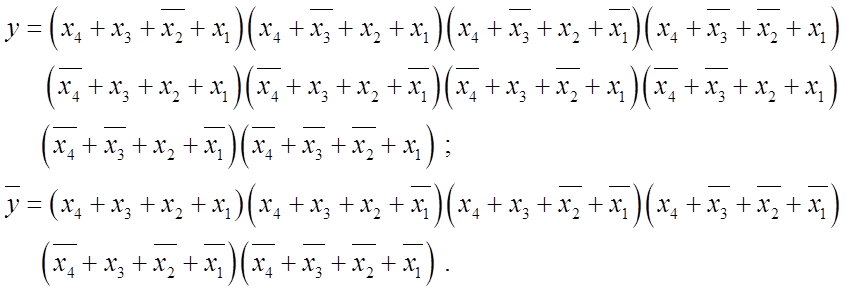
2.2 Мінімізація функції в чотирьох формах (МДНФ і МКНФ для прямої та інверсної форми)

Так як у мене функція чотирьох змінних , то діаграма термів мусить бути розмірності . Тобто така, у якій має місце шістнадцять змінних.

          Обчислимо МДНФ, знайдемо значення функції:

 

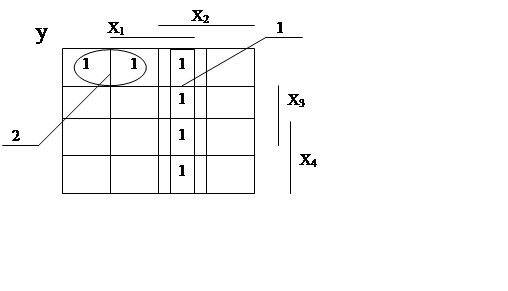Рисунок 1.1 - Обчислення прямого значення МДНФ

          На рисунку 1.1 зображено об’нання одиниць, яким користувався для створення МДНФ прямої форми. В даній формі якщо проти усього об’єднання знаходиться змінна, то вона записується без інверсії, а коли навпаки – без інверсії.Причому до терму входять ті змінні, які протягом усього об’єднання мають стале значення, а ті що змінюються – взагалі не входять. Врахувавши це можна записати, що МДНФ прямої форми буде:

          При обчисленні МДНФ для інвертованого значеня функції я користувався об’єднанням нулів функції (рисунок 1.2). Враховуючи те, що це є диз’юнктивна форма (а отже її функція є конституєнтою одиниці), скористався попередніми правилами. Отже МДНФ інверсної форми матиме такий запис: