Проектування цифрових пристроїв на типових ІС та на ВІС програмованої структури, страница 6

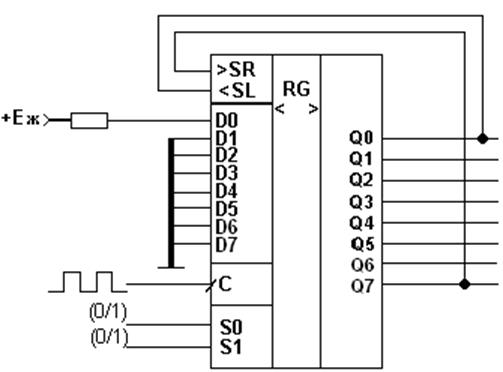
Наведемо перемикальну таблицю (на вхід подаємо 00000001):

С	S0	S1	D0	D1..D7	Q0	Q1	Q2	Q3	Q4	Q5	Q6	Q7	SR	SL
01	1	1	1	0	1	0	0	0	0	0	0	0	0	0
01	1	0	1	0	0	1	0	0	0	0	0	0	0	0
01	1	0	1	0	0	0	1	0	0	0	0	0	0	0
01	1	0	1	0	0	0	0	1	0	0	0	0	0	0
01	1	0	1	0	0	0	0	0	1	0	0	0	0	0
01	1	0	1	0	0	0	0	0	0	1	0	0	0	0
01	1	0	1	0	0	0	0	0	0	0	1	0	0	0
01	1	0	1	0	0	0	0	0	0	0	0	1	1	0
01	1	0	1	0	1	0	0	0	0	0	0	0	0	0
01	1	0	1	0	0	1	0	0	0	0	0	0	0	0
01	0	1	1	0	0	0	1	0	0	0	0	0	0	0
01	0	1	1	0	0	1	0	0	0	0	0	0	0	0
01	0	1	1	0	1	0	0	0	0	0	0	0	0	1
01	0	1	1	0	0	0	0	0	0	0	0	1	0	0
01	0	1	1	0	0	0	0	0	0	0	1	0	0	0
01	0	1	1	0	0	0	0	0	0	1	0	0	0	0
01	0	1	1	0	0	0	0	0	1	0	0	0	0	0
01	0	1	1	0	0	0	0	1	0	0	0	0	0	0
01	0	1	1	0	0	0	1	0	0	0	0	0	0	0
01	0	1	1	0	0	1	0	0	0	0	0	0	0	0

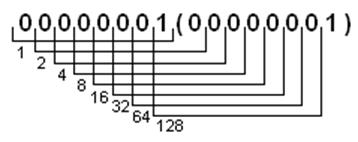Будуємо перемикальний граф:

Визначаємо коди які будуть утворюватись на виході регістра, зважаючи на схему визначення бачимо, що

N = 1, 2, 4, 8, 16, 32, 64, 128. Якщо регістр працюватиме у реверсивному режимі, відповідно будемо мати N = 128, 64, 32, 16, 8, 4, 2, 1.

Перемикальний граф  ГКП, де „” -  позначає прямий хід, а „” – зворотний:

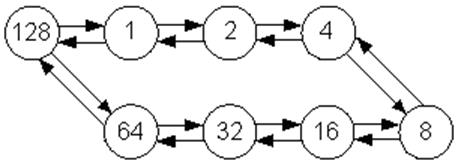
Перевіримо отриманий регістр на самовідновність, виходячи з формули:За формулою:

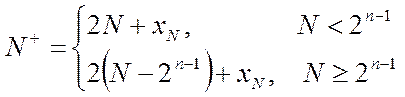
Перевіряємо стани, в яких РІР не перебуває. Дана функція на самовідновність перевірена, і є самовідновною. Дані по перевірці не приводяться оскільки їх дуже багато. Повний перемикальний граф не приводиться з аналогічної причини.

Будуємо часові діаграми: