Також дуже важливими для якості розробленого пристрою є теоретичні принципи його побудови. Одну і ту саму функцію можна реалізувати кількома схемними рішеннями, матеріальні виконання яких не завжди тотожні. Тому однією з найважливіших задач розробника є розгляд якомога більшого числа варіантів і вибір оптимального із них як за швидкодією, так і за вартістю.
Типові елементи логічних пристроїв служать основою для побудови цифрових обчислювальних машин та автоматів дискретної дії. Логічні елементи здійснюють перетворення логічних сигналів, елементи пам’яті - запам’ятовування інформації. Логічні пристрої можна розділити на комбінаційні та послідовнісні. Комбінаційні логічні пристрої складаються з логічних елементів; вихідний сигнал залежить тільки від вхідних сигналів в розглянумий момент часу. Послідовнісні логічні пристрої окрім логічних елементів вміщують і елементи пам’яті; вихідний сигнал залежить не тільки від вхідних сигналів в розглянутий момент часу, але й від напруги на виводах елементів пам’яті, яка є результатом логічної обробки сигналів, поступаючих в попередні моменти часу.
1 Спроектувати пристрій на логічних елементахдля логічної функції ![]()
 1.1
Навести досконалу форму (ДДНФ або ДКНФ) і таблицю відповідності для заданої
функції.
1.1
Навести досконалу форму (ДДНФ або ДКНФ) і таблицю відповідності для заданої
функції.
Мінімізуємо задану функцію(ДДНФ): у
![]()
![]()
![]()
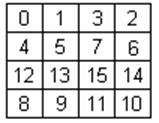
Складаємо таблицю відповідності:
|
i |
X4 |
X3 |
X2 |
X1 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
|
2 |
0 |
0 |
1 |
0 |
0 |
|
3 |
0 |
0 |
1 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
0 |
|
5 |
0 |
1 |
0 |
1 |
1 |
|
6 |
0 |
1 |
1 |
0 |
0 |
|
7 |
0 |
1 |
1 |
1 |
0 |
|
8 |
1 |
0 |
0 |
0 |
1 |
|
9 |
1 |
0 |
0 |
1 |
0 |
|
10 |
1 |
0 |
1 |
0 |
1 |
|
11 |
1 |
0 |
1 |
1 |
0 |
|
12 |
1 |
1 |
0 |
0 |
1 |
|
13 |
1 |
1 |
0 |
1 |
0 |
|
14 |
1 |
1 |
1 |
0 |
0 |
|
15 |
1 |
1 |
1 |
1 |
0 |
По складеній таблиці наведемо вирази для логічної функції Y:
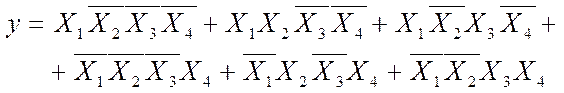 |
ДКНФ:
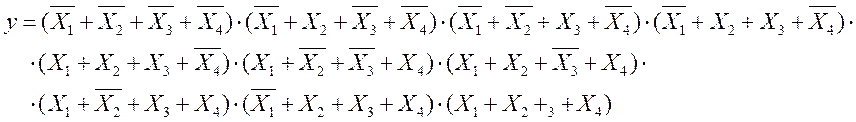
1.2 Мінімізувати функцію у формі (МДНФ / МКНФ для прямого / інверсного її зображення), потрібній для реалізації в базисах І-НЕ, АБО-НЕ, І-АБО-НЕ та навести схеми в цих базисах із зазначенням їх складності.
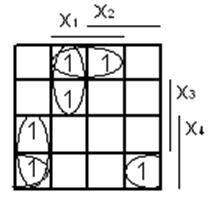
По таблиці відповідності складаємо відповідні діаграми термів, щоб записати МДНФ і МКНФ:
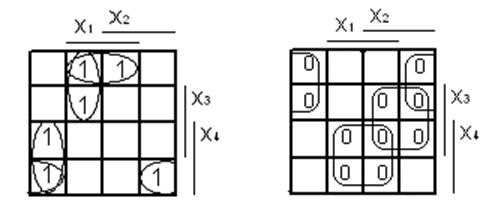
МДНФ: ![]()
МДНФ (інверсна): ![]()
МКНФ: ![]()
МКНФ (інверсна): ![]()
Зображаємо схему функції (після мінімізації функції) у базисі І-НЕ:
Мінімізуємо функцію у базисі І-НЕ:
![]()
![]()
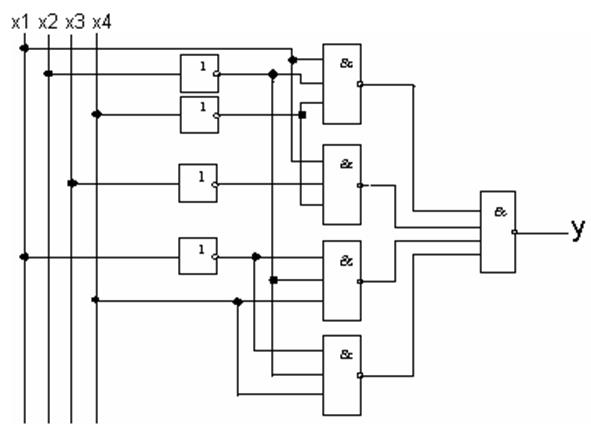 |
В результаті видно, що складність даної схеми, становить: 9/20
Зображаємо схему функції у базисі АБО-НЕ:
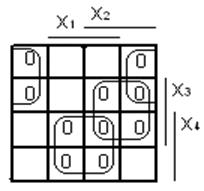 Мінімізуємо функцію
у базисі АБО-НЕ:
Мінімізуємо функцію
у базисі АБО-НЕ:
![]()
![]()
В результаті видно, що складність даної схеми, становить: 8/13
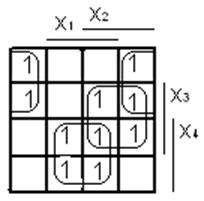 Зображаємо
схему функції у базисі І-АБО-НЕ:
Зображаємо
схему функції у базисі І-АБО-НЕ:
Мінімізуємо функцію у базисі І-АБО-НЕ:
![]()
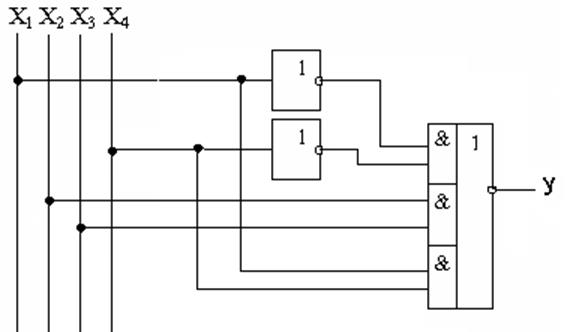
В результаті видно, що складність даної схеми, становить: 3/8
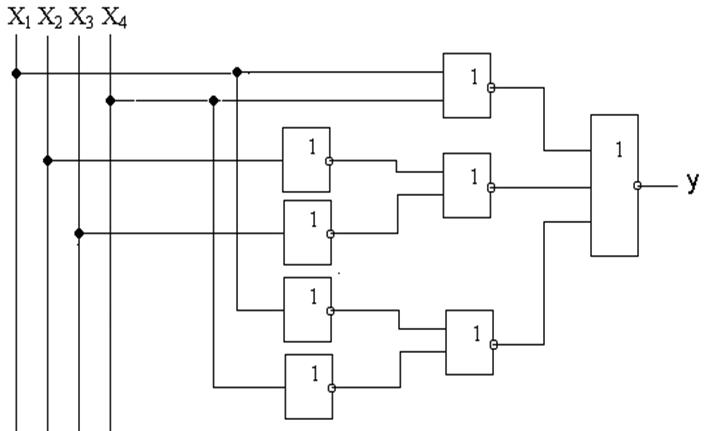
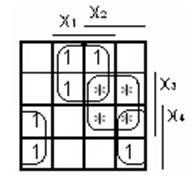
1.3 Мінімізувати схему в одному елементному базисі (І-НЕ чи АБО-НЕ), що забезпечує меншу складність, порівняти її зі складністю схем за п. 1.2.
Зображаємо схему функції після виконання редукції у базисі I-НЕ:
![]()
![]()
![]()
![]()
![]()
![]()
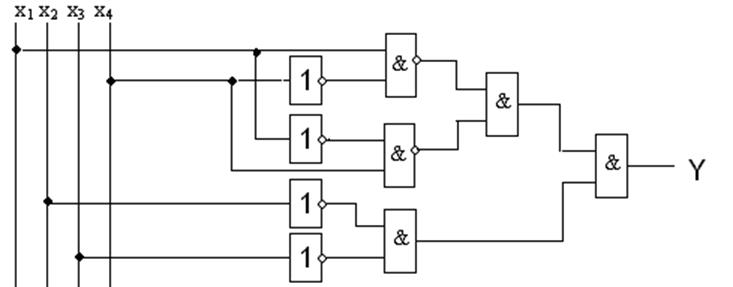
В результаті видно, що складність даної схеми, становить: 9/14
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.