Санкт-Петербургский государственный политехнический университет
Кафедра Теоретической Электротехники
Расчётное задание №1
“Расчёт схемы с помощью законов Кирхгоффа, метода контурных токов, метода узловых напряжений и метода сечений”.
Выполнил: студент группы 4027/3
Бельский Р.А
Преподаватель: Адалев А.С.
Санкт-Петербург
2011
Таблица 1. Начальные условия
|
Ветвь |
Узлы |
Параметры |
|||||
|
начало |
конец |
R |
L |
C |
E |
J |
|
|
1 |
2 |
1 |
|
|
|||
|
2 |
3 |
2 |
|
|
|||
|
3 |
4 |
2 |
|
|
|
||
|
4 |
7 |
2 |
|
||||
|
5 |
1 |
7 |
|
||||
|
6 |
7 |
3 |
|
|
|
||
|
7 |
4 |
7 |
|
||||
|
8 |
4 |
6 |
|
|
|||
|
9 |
5 |
4 |
|
|
|||
|
10 |
6 |
5 |
|
||||
|
11 |
7 |
6 |
|
||||
|
12 |
4 |
3 |
|
||||
Таблица 2. NET лист. Без идеального источника тока
|
Ветвь |
Узлы |
Параметры |
|||||
|
начало |
конец |
R |
L |
C |
E |
J |
|
|
1 |
2 |
1 |
|
|
|
||
|
2 |
3 |
2 |
|
|
|||
|
3 |
4 |
3 |
|
||||
|
4 |
5 |
4 |
|
|
|||
|
5 |
6 |
5 |
|
||||
|
6 |
7 |
6 |
|
||||
|
7 |
7 |
2 |
|
|
|||
|
8 |
7 |
3 |
|
|
|
||
|
9 |
4 |
7 |
|
||||
|
10 |
4 |
6 |
|
|
|||
|
11 |
4 |
2 |
|
|
|
||
Таблица 3. NET лист. Без идеального источника ЭДС
|
Ветвь |
Узлы |
Параметры |
|||||
|
начало |
конец |
R |
L |
C |
E |
J |
|
|
1 |
2 |
1 |
|
|
|||
|
2 |
3 |
2 |
|
|
|||
|
3 |
4 |
3 |
|
||||
|
4 |
5 |
4 |
|
|
|
||
|
5 |
6 |
5 |
|
||||
|
6 |
1 |
6 |
|
||||
|
7 |
6 |
2 |
|
||||
|
8 |
6 |
3 |
|
|
|
||
|
9 |
4 |
6 |
|
||||
|
10 |
4 |
5 |
|
|
|||
|
11 |
4 |
2 |
|
|
|
||
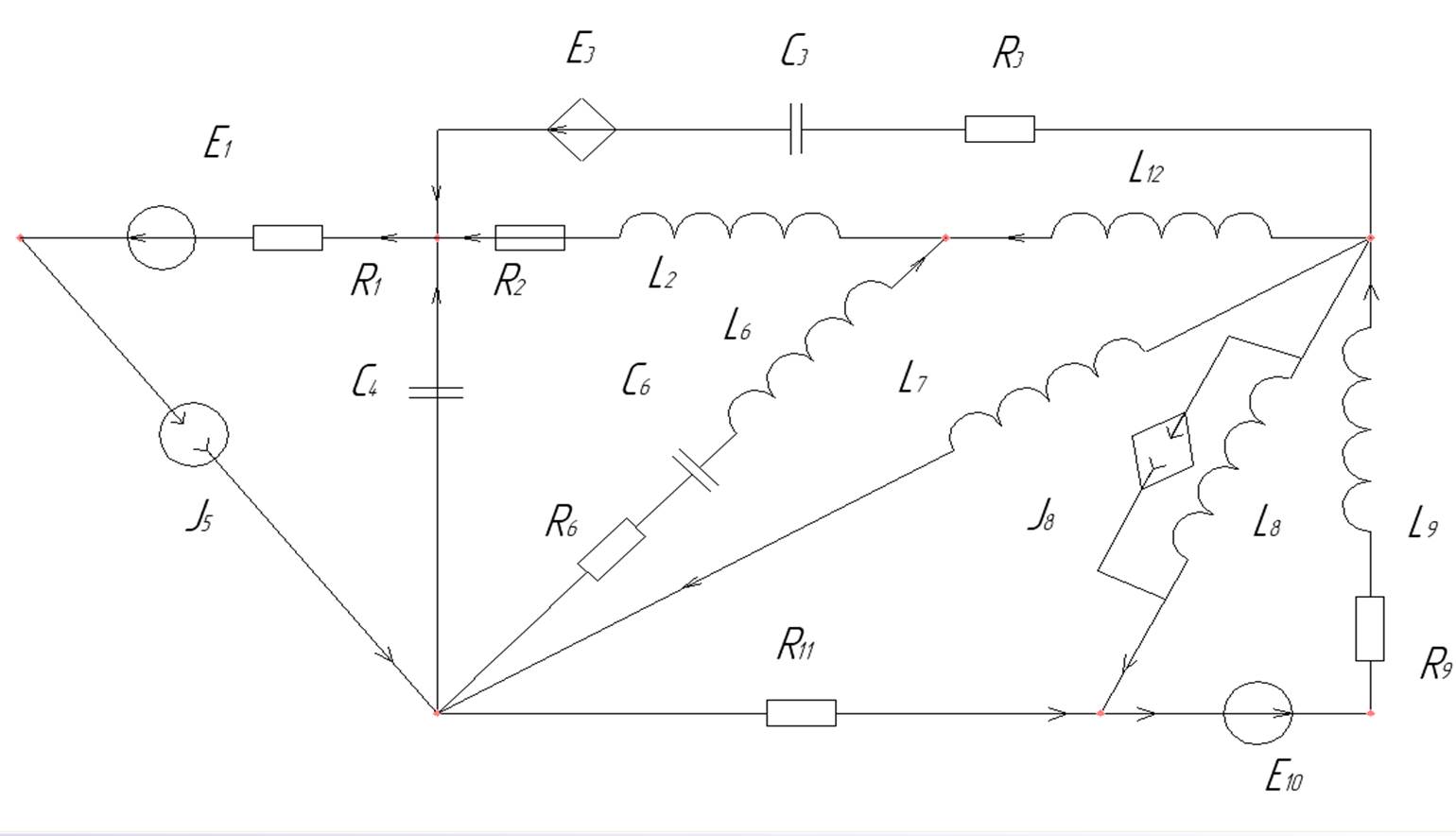
Рисунок 1. Общая схема
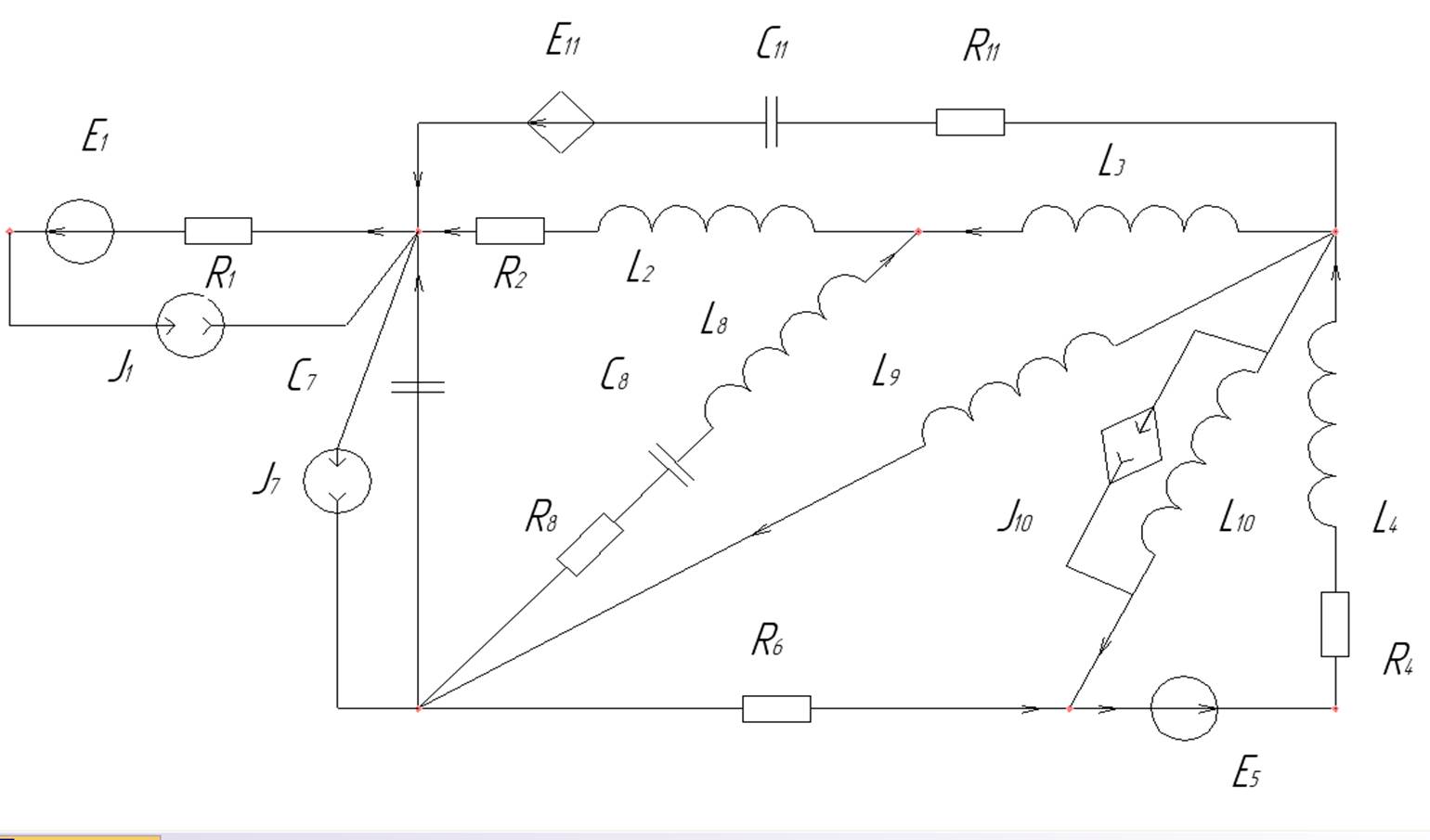
Рисунок 2.Схема без идеального источника тока для решения через закон Кирхгоффа и метод контурных токов.
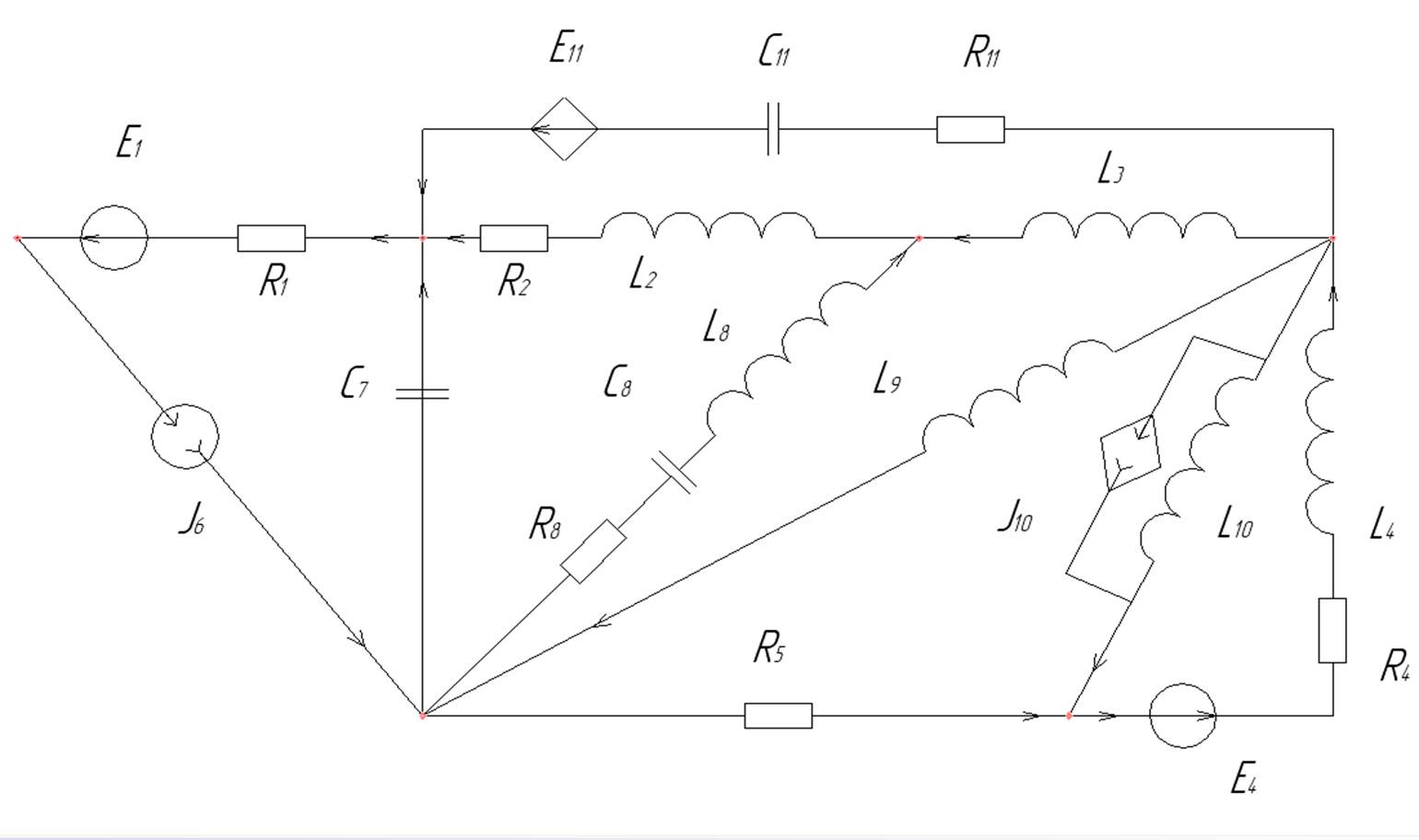
Рисунок 3.Схема без идеального источника ЭДС для решения методом сечения и методом узловых напряжений.
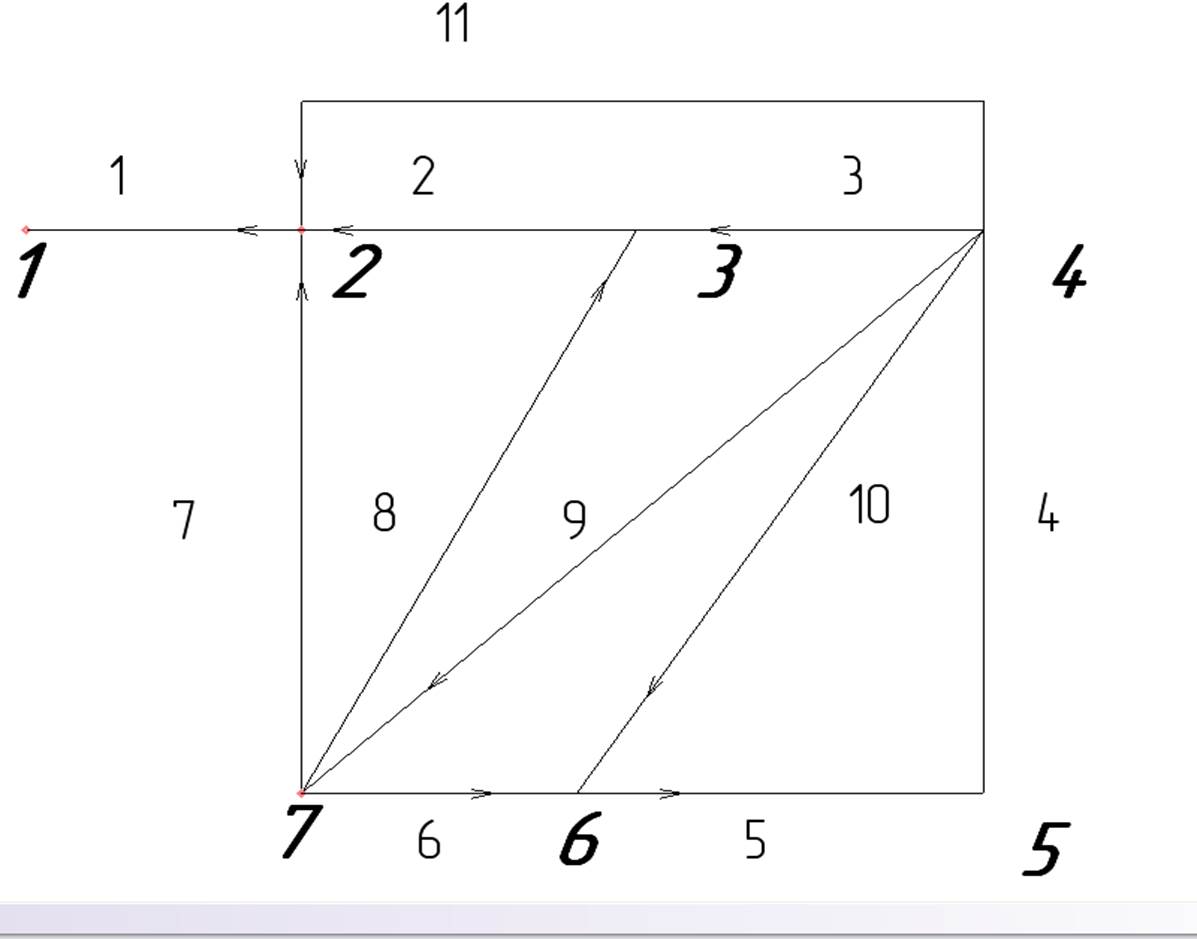
Рисунок 4. Граф схемы без идеального источника тока
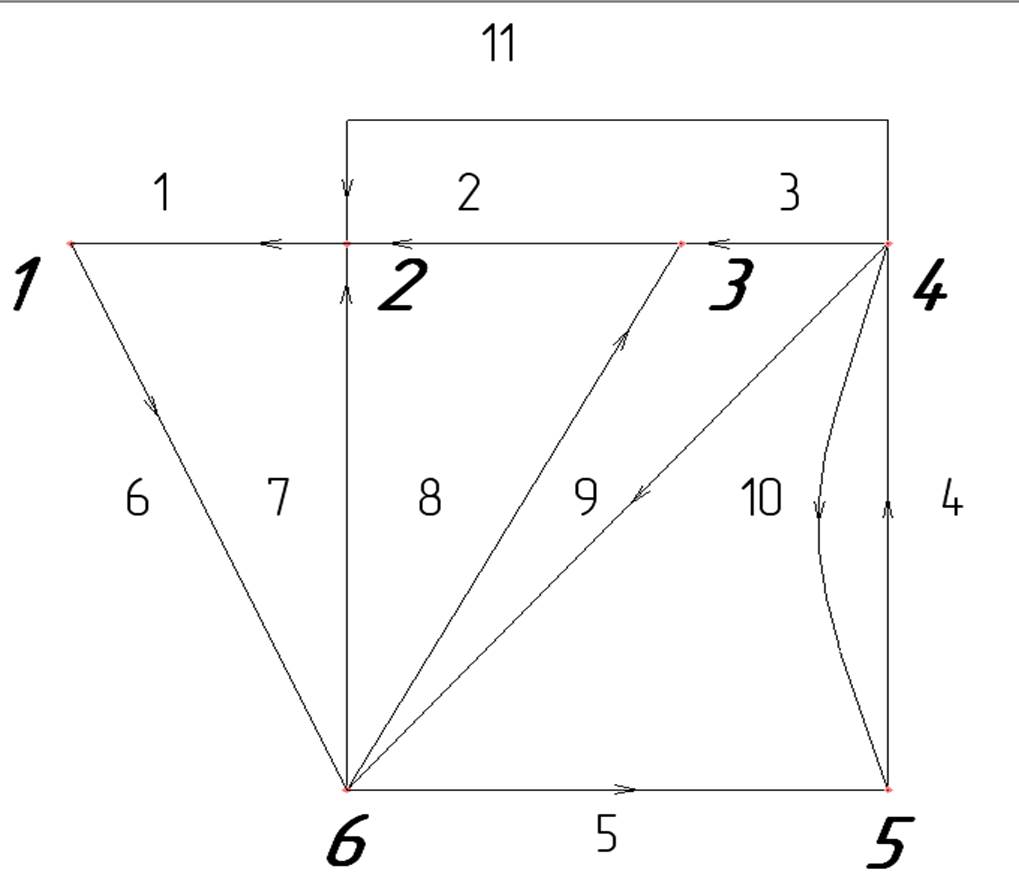
Рисунок 5. Граф схемы без идеального источника ЭДС
Закон Кирхгоффа.
1) Составляем NET лист.
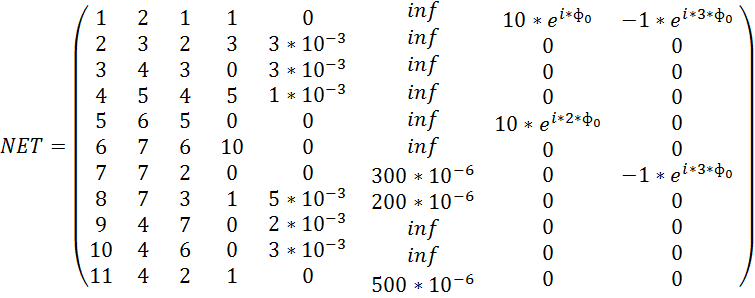
2) Выделим матрицы ![]() .
.
![]()
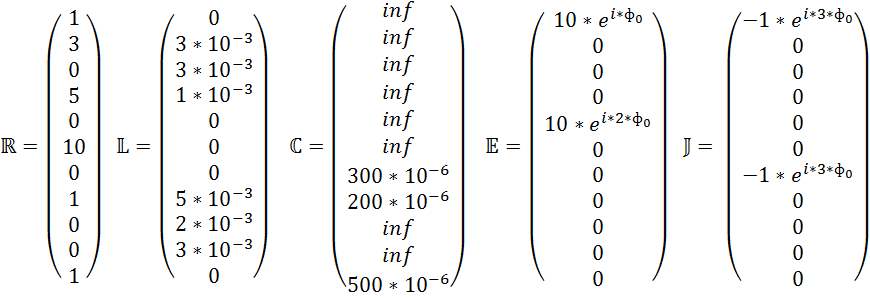
3) Составляем матрицу сопротивлений.
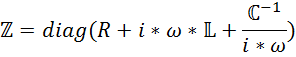
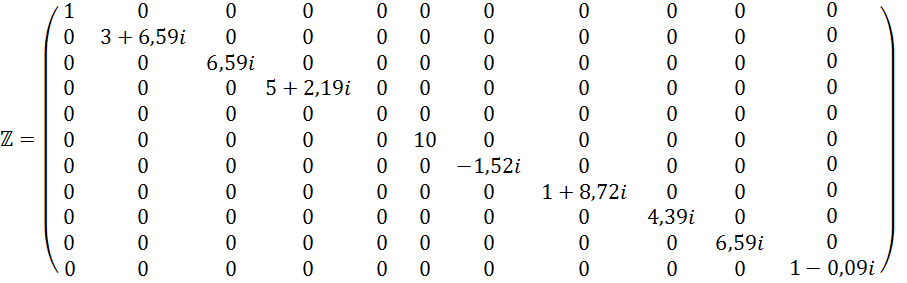
Составляем матрицу узловых соединений .
Для начала необходимо написать программу, которая заполнит ячейки.
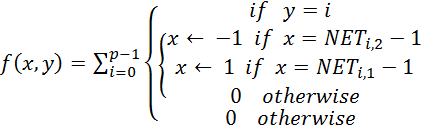
![]()
![]()
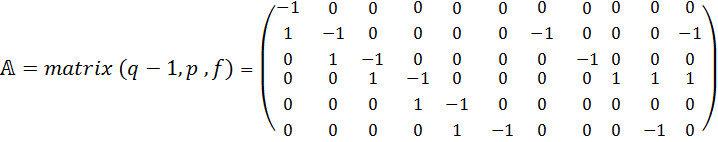
4) Разделяем на две субматрицы
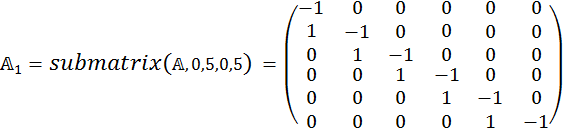
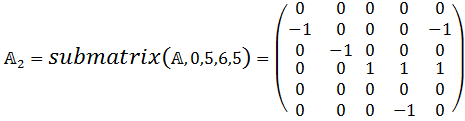
5) Выводим матрицу F
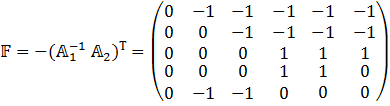
6) Выводим матрицу контуров С
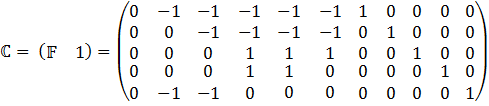
7) Выводим матрицу сечений D
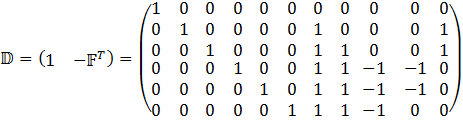
8) Составляем матрицы коэффициентов пропорциональности
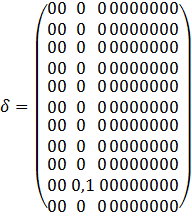
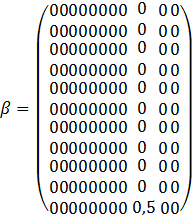
9) Решение закона Кирхгоффа. Для цепи без зависимых источников.
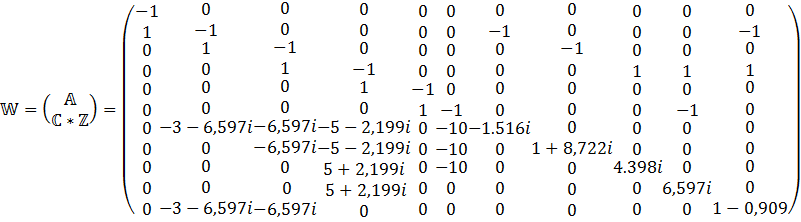
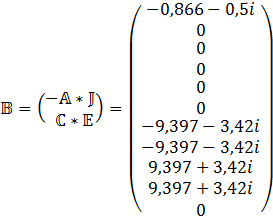
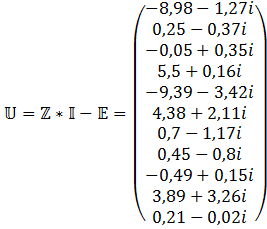
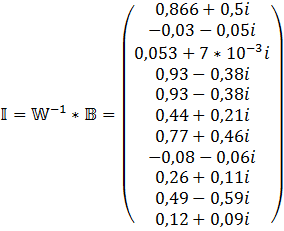
10) Решение закона Кирхгоффа. Для цепи с зависимых источников.
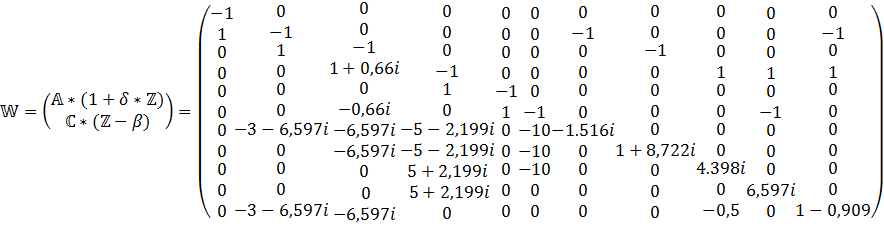
Также необходимо учесть зависимые источники
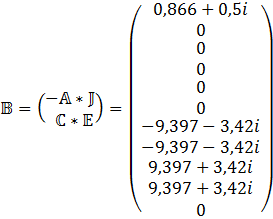
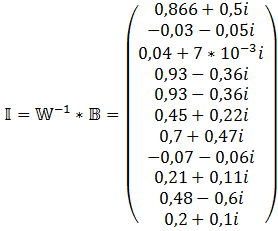
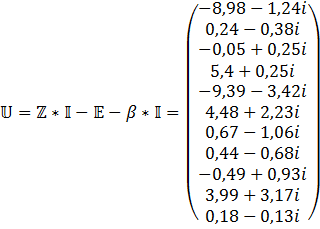
Метод контурных токов.
1) Матрицы узловых соединений А, матрицу F, контуров С, сечений D а также матрицы β и Δ возьмём из решений законов Кирхгоффа.
На основе этих данных запишем матрицу решения контурных токов для цепи без зависимого источника
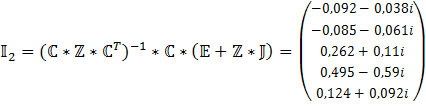
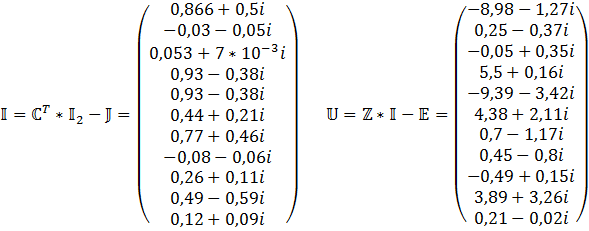
2) Запишем матрицу решения контурных токов для цепи с зависимым источником
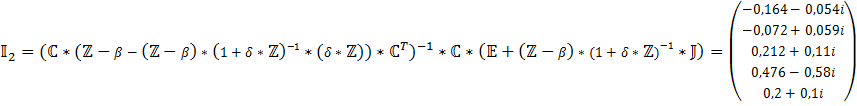
3) Решение МКТ
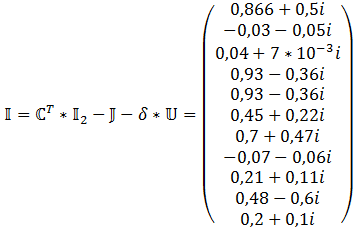
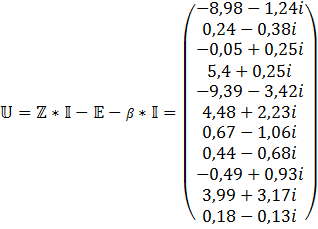
Метод узловых напряжений.
1) Составляем NET лист.
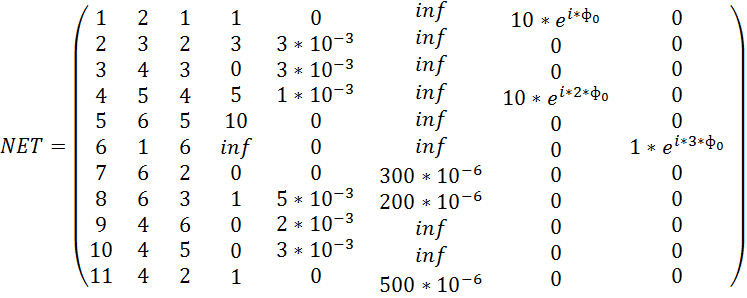
2) Выделим матрицы ![]() .
.
![]()
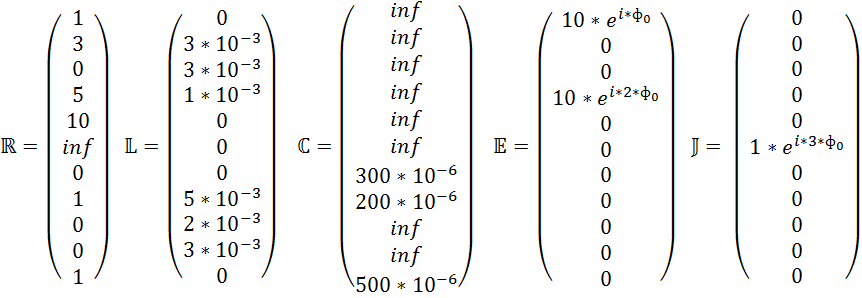
3) Составляем матрицу сопротивлений.
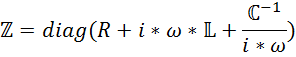
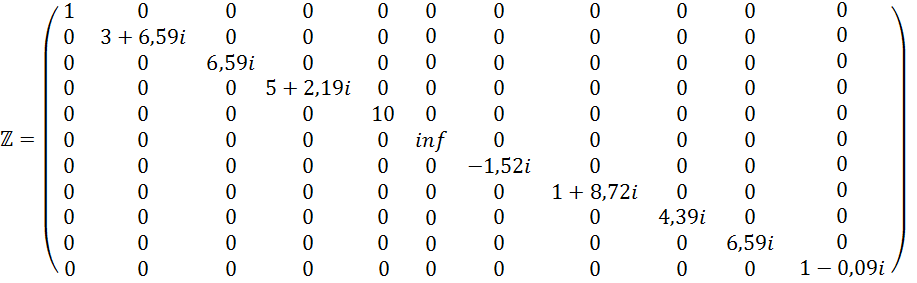
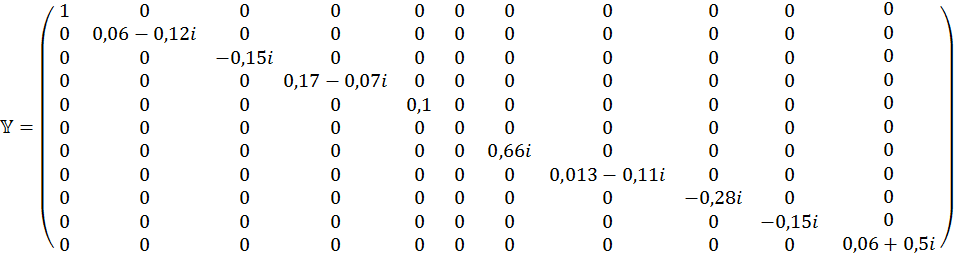
11) Составляем матрицу проводимости.
![]()
4) Составляем матрицу узловых соединений .
Для начала необходимо написать программу, которая заполнит ячейки.
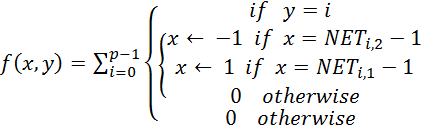
![]()
![]()
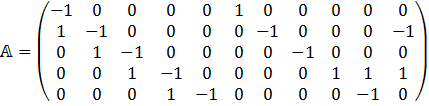
5) Разделяем на две субматрицы
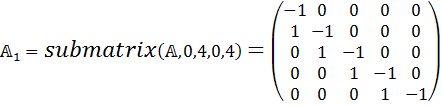
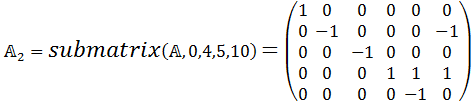
6) Выводим матрицу F
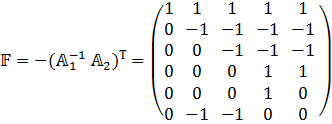
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.