Основные свойства определенного интеграла по отрезку. Теорема об оценке. Теорема о среднем. Теорема Барроу, страница 5

В этом случае мы непосредственно получаем только одно решение . Докажем, что в качестве второго решения можно взять функцию . Продифференцируем дважды функцию :

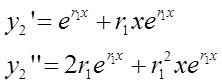
Подставив данные выражения в левую часть уравнения:

.

Поскольку  корень характеристического уравнения, то ; а так как  - двукратный корень, то по формуле Виета . Таким образом выражение заключенное в скобках равно 0, и функция  действительно является решением уравнения.

В случае действительных, равных корней общее решение имеет вид:

.

Билет №37

Линейные однородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами, Ф.С.Р. и общее решение в случае комплексных корней, характеристические уравнения с доказательством.

Корни характеристического уравнения комплексные сопряженные числа.

Для комплексных корней общее решение можно записать так

Для того чтобы получить решение в действительной форме, воспользуемся следующим простым правилом: если уравнение с действительными коэффициентами имеет комплексное решение , то каждая функция является решением этого уравнения.

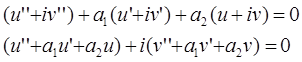
Комплексное выражение равно 0 только тогда, когда равны 0 его действительная и мнимая части, а это и значит, что функции являются решениями. Так как по формуле Эйлера:

то это и будет решением данного уравнения. В случае комплексных корней характеристического уравнения общее решение имеет вид:

Билет №38

Линейные неоднородные дифференциальные уравнения 2-ого порядка, метод вариации произвольных постоянных с доказательством.

Неоднородное уравнение – значит с правой частью. Общее решение такого уравнения складывается из общего решения соответствующего уравнения без правой части и какого-нибудь частного решения уравнения с правой частью. Но правая часть может иметь разный вид. Рассмотрим некоторые.

1) пусть правая часть имеет вид: . Тогда уравнение имеет частное решение вида .

2) правая часть имеет вид: . Если числа  не являются корнями, то уравнение имеет частное решение вида . Если же эти числа не являются корнями, то просто надо домножить на х.

3) правая часть имеет вид: . Если числа  не являются корнями уравнения, то общее решение имеет вид: , если же эти числа являются решениями, то надо домножить на х.

Метод вариации произвольных постоянных.

Этот метод дает возможность найти как частное, так и общее решение уравнения. Известно, что общее решение уравнения . Если С₁ и С₂ определяются из одного уравнения, то для определения 2-х функций одну из них определяем произвольно. Продифференцируем равенство:

Продифференцируем еще раз

Подставим в левую часть уравнения

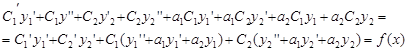
Выражения в обеих скобках равны 0, так как  - являются решениями уравнения без правой части. Значит чтобы функция  была решением, должно соблюдаться условие

Таким образом, мы приходим к системе уравнений

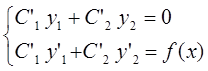
Билет №39

Система функций является линейно независимой, если ни одну из этих функций нельзя представить в виде линейной комбинации остальных. Из этого следует, что ни одна из функций не может равняться 0. Система функций не являющаяся линейно независимой называется линейно зависимой. Существует простое условие линейной независимости частных решений. Именно, этим условием служит неравенство нулю определителя Вронского, составленного из функций  и их производных. Определитель не может равняться 0, ни при каком значении х.  Этот определитель играет важную роль при отыскании частного решения по заданным начальным условиям.