Основные свойства определенного интеграла по отрезку. Теорема об оценке. Теорема о среднем. Теорема Барроу, страница 2

Дифференциальные уравнения 1-го порядка.

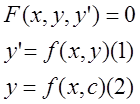
Общим решением дифференциального уравнения называется совокупность функций зависящих от х и константа С, которая удовлетворяет дифференциальным уравнениям при любых С.

Частное решение:

Если С – число, то  эти функции зависят от х.

Задача Коши для дифференциального уравнения 1-го порядка.

Из общего решения (2) можно выделить частное решение, для этого необходимо задать начальные условия.

Начальное условие 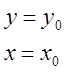 или .

Теорема Коши (о существовании единственного решения дифференциального уравнения).

Если функция (1) непрерывна в области Д на плоскости ХОУ содержит точку , то уравнение  имеет решение  соответствующую начальным условиям, имеет решение если кроме этого непрерывна и частная производная , то это решение единственно ( - частное решение).

О.4 Частным решением называется функция  которая:

1.  удовлетворяет дифференциальному уравнению

2.  начальным условиям.

Геометрическая иллюстрация решения дифференциального уравнения 1-го порядка.

Имеется дифференциальное уравнение 1-го порядка  и обозначим решение  - это есть множество интегральных кривых.

 - это одна из кривых проходящая через точку  

1)

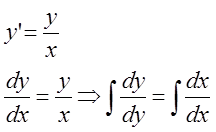
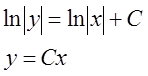
Пучек прямых:

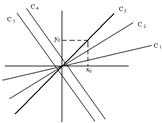
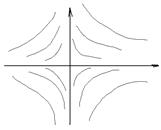
Т(0,0) – седло, Т – особая. Точки, в которых условия теоремы не выполняются называются особыми.

Билет №25

Дифференциальные уравнения, в которых переменные можно разделить посредством умножения обеих частей на одно и то же выражение, называются дифференциальными уравнениями с разделяющимися переменными.

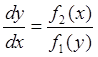
деля обе части уравнения на произведение , получим

,

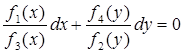интегрируя, запишем:

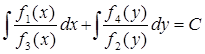
уравнение 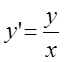 имеет общее решение , т.е. совокупность прямых проходящих через начало координат, за исключением прямой х=0 – оси ординат.

Билет №26

Уравнение вида , т.е. линейное относительно искомой функции и ее производной называется линейным. Здесь  и  - известные функции независимой переменной х.

Уравнение сводится к двум уравнениям с разделяющимися переменными следующим путем: заменяют . Соответственно . Подставляя эти выражения в уравнения, получаем:

 или .

Выберем в качестве  какое-нибудь частное решение уравнения:

тогда для отыскания  получим уравнение: .

Сначала найдем  из уравнения . Разделяя переменные, имеем

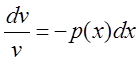
откуда

 и .

Зная , находим далее  из уравнения (***):

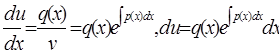 и значит,

.

По u и v находим искомую функцию у:

.

Полученная формула дает общее решение линейного уравнения.

Билет №27

Уравнения Бернулли.

.

При n=0, это линейное уравнение, а при n=1 можно разделить переменные. При других значениях n оно сводится к линейному при помощи следующего приема: делим обе части уравнения на  и записываем его так:

.

Если внести вспомогательную неизвестную функцию , то , и уравнение примет вид

.

Это линейное уравнение; решая его и переходя от z снова к y, мы и получим решение исходного уравнения.

Билет №28

Поле направлений определяемое уравнением y`=f(x,y). Изоклины, метод Эйлера, приближенного решения з. Каши для уравнения y`=f(x,y).

Если ни один из приемов решения дифференциального уравнения не приводит к его решению, то можно прибегнуть к приближенному решению этого уравнения. Уравнение  определяет в каждой точке плоскости ХОУ, в которой справедлива теорема существования единственности решения, величину углового коэффициента касательной к интегральной кривой, проходящей через точку . Эту величину можно изобразить прямолинейной стрелкой. Таким образом, заданием уравнения устанавливается поле направлений в плоскости ХОУ. Геометрическое место точек с одинаковым направлением поля называется изоклиной (линией равных наклонов) уравнения. Мы получим уравнение изоклины, соответствующей данному значению , если подставим это значение в дифференциальное уравнение.

Графический метод Эйлера.