Основные свойства определенного интеграла по отрезку. Теорема об оценке. Теорема о среднем. Теорема Барроу, страница 3

Задача сводится к отысканию частного решения уравнения 1 с начальными условиями. Для этого проделаем следующие однотипные построения.

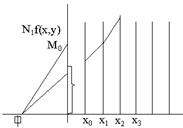
Разобьем интервал х₀, х на n частей точками x₀, x₂, x₃ и т.д. Через точки деления проведем прямые параллельные оси у. Вычислим значения  в точке М₀, тогда значения  - тангенс угла наклона или угловой коэффициент. Для построения направлений возьмем некоторый полис Ф по оси ОХ и отстоящий от него на расстояние . На оси ОУ в масштабе ОФ отложим значения функции. Подставим точку М₀, соединим ее с полюсом Ф. Из точки  проведем прямую параллельную  до пересечения с х1. Вычислим значения функции в точке х1. Отложим значения Ф от х₁,у₁ по оси У в масштабе ОФ, получим точку, соединим полюс Ф с точкой Ф₁ линии. Из точки М₁ проведем прямую, параллельную ФМ₁, до пересечения с прямой х=х₂. Аналогичные построения, в конечном счете, дают ломаную линию, которая заменяет интегральную кривую.               

 Билет №29

Уравнения высших порядков, з. Каши для уравнения y``=f(x,y,y`) и её геометрические интерпретации. Общее и частное решение дифференциального уравнения 2-ого порядка.

О.1 Дифференциальным уравнением n-го порядка называется уравнение, связывающее искомую функцию у и ее первых n производных.

(3)  - разрешенное.

О.2 Общим решением дифференциального уравнения n-го порядка называется функция , такая что:

1) удовлетворяет дифференциальному уравнению при любых С.

2) при задании начальных условий постоянную С можно найти так чтобы функция удовлетворяла и дифференциальному уравнению и начальным условиям.

Начальные условия:

.

Теорема Коши. 

Если в уравнении (3) функция  непрерывна со своими частными производными в некоторой области содержащей значения при , то существует единственное решение, удовлетворяющее начальным условиям.  - которое называется частным решением дифференциального уравнения (3).

О.4 Всякая функция, полученная из общего решения при конкретных С называется частным решением.

Билет №31

Линейная зависимость и независимость системы функций. Фундаментальная система решений(Ф.С.Р) линейного однородного дифференциального уравнения 2-ого порядка, определение. Определитель Бронского.

Теория для решения однородного дифференциального уравнения второго порядка может быть перенесена для решения уравнений n-го порядка.

 - однородное линейное уравнение n-го порядка. Чтобы сформулировать основную теорему о структуре общего решения, введем понятие линейной независимости системы функции.

О.1 Система функций  определенная в одном и том же интервале называется линейно независимой если ни одну из них нельзя представить в виде линейной комбинации остальных.

О.2 Фундаментальной системой уравнения называется система n линейно независимых частных решений .

Теорема.

Если {y_n} есть n частных, линейно независимых решений уравнения, образующих фундаментальную систему решений, то общее решение дифференциального уравнения есть линейная комбинация этих функций.

 (6) – общее решение дифференциального уравнения n-го порядка.

Доказательство проводится аналогично доказательства дифференциального уравнения второго порядка. Условие линейной независимости частных решений следует из неравенства нулю определителя Вронского. Этот определитель играет важную роль при отыскании частного решения при заданных начальных условиях. Т.к. определитель не равен 0, то решение единственно. Для перехода к системе необходимо домножить первый столбец на С₁, второй на С₂ и т.д.

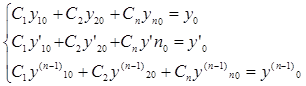
Билет №32

Свойства решений линейного однородного дифференциального уравнения с доказательством.

Докажем основное свойство однородного линейного дифференциального уравнения второго порядка. Из общего решения, всегда можно выделить частное решение при любых заданных возможных начальных условиях. Пусть заданы начальные условия (). Х₀ принадлежит интервалу, где функции непрерывны, т.е. выполняется условие существования и единственности теоремы Коши. Если а₁ и а₂ числа, то х₀ – любая точка. Подставим начальные условия в выражение для общего решения и ее производную. Получим систему относительно неизвестных С₁ и С₂: