Об усталостной прочности лопасти несущего винта вертолета при действии ветровых нагрузок
А.И. Братухина
Статья посвящена рассмотрению вопроса о напряжениях в невращающейся лопасти и втулке несущего винта вертолета под действием ветровых нагрузок. Сделано допущение, что вертолет находится на стоянке и его винт не вращается. Расчет проводился для несущего винта с шарнирным креплением лопастей. Решена задача о собственных и вынужденных колебаниях лопасти вертолета. Определены деформации и внутренние усилия (изгибающие моменты и напряжения в лонжероне лопасти). Проведен анализ результатов и оценено влияние швартовки лопасти в наземных условиях эксплуатации.
В данной работе рассмотрены случаи нагружения элементов конструкции лопасти и втулки в наземных условиях. Потребность в подобных расчетах всегда существует, в связи с постоянно встречающимися в эксплуатации повреждениями винтов при работе вертолета на земле.
Необходимость рассматривать наземные случаи нагружения вертолета подтверждена в "Нормах летной годности гражданских вертолетов", а также требованиями по сертификации, предъявляемыми за рубежом.
Рассматривается задача определения деформаций и внутренних усилий (изгибающих моментов и напряжений) в лонжероне лопасти несущего винта вертолета под действием ветровых нагрузок. Предполагается, что вертолет находится на стоянке и его винт не вращается. В некоторый момент времени на лопасть действует порыв ветра. Под действием порыва ветра на лопасти возникает аэродинамическая подъемная сила, которая в зависимости от направления ее действия, поднимает лопасть вверх или прижимает вниз. В результате этого лопасть совершает вынужденные колебания в вертикальной плоскости, а лонжерон нагружается изгибающим моментом, действующим в основном в плоскости наименьшей жесткости.
Расчет проводился для несущего винта с шарнирным креплением лопастей.
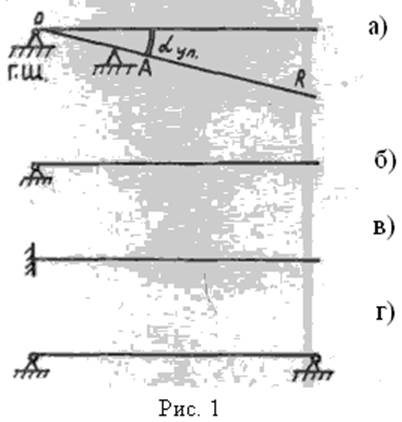
Движение лопасти относительно горизонтального шарнира происходит свободно до
некоторого положения, характеризуемого углом ограничителя свеса ![]() (рис. 1а). После этого перемещение
лопасти может происходить только за счет ее упругих деформаций. Таким образом,
если колеблющаяся под действием внешней нагрузки лопасть находится выше линии
OR, то ее движение описывается расчетной схемой, показанной на рис. 1б. После
того, как точка А комля лопасти достигла упора ограничителя свеса, ее
дальнейшее движение должно быть описано схемой, изображенной на рис. 1в. Для
зашвартованной лопасти расчетная схема соответствует рис. 1г.
(рис. 1а). После этого перемещение
лопасти может происходить только за счет ее упругих деформаций. Таким образом,
если колеблющаяся под действием внешней нагрузки лопасть находится выше линии
OR, то ее движение описывается расчетной схемой, показанной на рис. 1б. После
того, как точка А комля лопасти достигла упора ограничителя свеса, ее
дальнейшее движение должно быть описано схемой, изображенной на рис. 1в. Для
зашвартованной лопасти расчетная схема соответствует рис. 1г.
Малые колебания лопасти невращающегося несущего винта вертолета описываются дифференциальным уравнением в частных производных [1] :
![]() . (1)
. (1)
В уравнении: ![]() - перемещение сечения лопасти в плоскости
наименьшей жесткости;
- перемещение сечения лопасти в плоскости
наименьшей жесткости; ![]() - изгибная жесткость сечения лопасти
относительно главной оси, лежащей в плоскости хорд;
- изгибная жесткость сечения лопасти
относительно главной оси, лежащей в плоскости хорд; ![]() - внешняя распределенная нагрузка:
- внешняя распределенная нагрузка:
![]() , (2)
, (2)
где
![]() - погонная масса лопасти;
- погонная масса лопасти;
![]() - погонная аэродинамическая нагрузка;
- погонная аэродинамическая нагрузка;
![]() - ускорение силы тяжести.
- ускорение силы тяжести.
После подстановки (2) в (1) получим
![]() (3)
(3)
Решение уравнения (3) представим в виде разложения в ряд по собственным формам колебаний [2] :
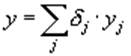 , (4)
, (4)
где ![]() -
число собственных форм, принимаемых в расчете;
-
число собственных форм, принимаемых в расчете;
![]() - форма
- форма ![]() - ого тона собственных колебаний лопасти в пустоте,
которая является функцией ее радиуса;
- ого тона собственных колебаний лопасти в пустоте,
которая является функцией ее радиуса;
![]() - некоторые функции времени (коэффициенты
деформаций).
- некоторые функции времени (коэффициенты
деформаций).
Собственные формы ![]() определяются из дифференциального уравнения
(3), когда его правая часть равна нулю:
определяются из дифференциального уравнения
(3), когда его правая часть равна нулю:
![]() (5)
(5)
После определения частот и форм собственных колебаний в решении (4),
неизвестными останутся только коэффициенты деформаций ![]() . Применяя метод Б.Г. Галеркина к
системе дифференциальных уравнений изгибных колебаний лопасти, записанных в
частных производных (3), после двукратного дифференцирования, получим:
. Применяя метод Б.Г. Галеркина к
системе дифференциальных уравнений изгибных колебаний лопасти, записанных в
частных производных (3), после двукратного дифференцирования, получим:
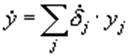 , (6)
, (6)
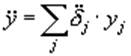 . (7)
. (7)
Подставим (4), (6) и (7) в уравнение (3), а затем умножим его поочередно на ![]() и проинтегрируем
по радиусу лопасти. В силу ортогональности собственных форм получим систему
обыкновенных дифференциальных уравнений, связанных между собой только через
аэродинамическую нагрузку:
и проинтегрируем
по радиусу лопасти. В силу ортогональности собственных форм получим систему
обыкновенных дифференциальных уравнений, связанных между собой только через
аэродинамическую нагрузку:
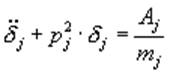 (8)
(8)
где
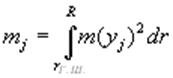 ;
;
![]() - частота собственных колебаний лопасти по
j-ому тону,
- частота собственных колебаний лопасти по
j-ому тону,
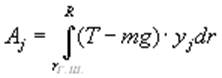 .
.
Расчет аэродинамических сил, входящих в правую часть уравнения (8),
выполняется в зависимости от аэродинамических коэффициентов подъемной силы ![]() и силы
сопротивления
и силы
сопротивления ![]() от угла атаки профиля лопасти и числа Маха,
полученных по результатам продувок в аэродинамических трубах. Вычисление
коэффициентов деформации лопастей
от угла атаки профиля лопасти и числа Маха,
полученных по результатам продувок в аэродинамических трубах. Вычисление
коэффициентов деформации лопастей ![]() выполняется методом численного
интегрирования уравнения (8).
выполняется методом численного
интегрирования уравнения (8).
Под действием ветровой нагрузки лопасть вертолета, находящегося на стоянке,
начинает движение в вертикальной плоскости. В зависимости от того, находится ли
лопасть на ограничителе свеса или отошла от него, в решении (4) используются
шарнирные или консольные формы колебаний. Коэффициенты деформации, определяемые
из системы дифференциальных уравнений (8), также будут соответствовать
шарнирным или консольным формам. При колебательном движении лопасти в момент
изменения консольных форм ![]() на шарнирные
на шарнирные ![]() и наоборот должно соблюдаться
условие сопряжения решений. Это может быть получено путем обеспечения равенства
перемещений и скоростей движения лопасти в момент смены форм. Обозначим
перемещения и скорости для шарнирно опертой лопасти через
и наоборот должно соблюдаться
условие сопряжения решений. Это может быть получено путем обеспечения равенства
перемещений и скоростей движения лопасти в момент смены форм. Обозначим
перемещения и скорости для шарнирно опертой лопасти через
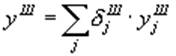 (9)
(9)
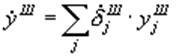 (10)
(10)
а для консольного закрепления
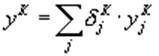 , (11)
, (11)
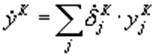 . (12)
. (12)
Приравнивая выражения (9), (11) для перемещений и (10), (12) для скоростей
движения и учитывая угол ![]() , получим после некоторых преобразований
начальные условия для коэффициентов деформации и их производных в момент
времени, когда лопасть поднимается с ограничителя свеса:
, получим после некоторых преобразований
начальные условия для коэффициентов деформации и их производных в момент
времени, когда лопасть поднимается с ограничителя свеса:
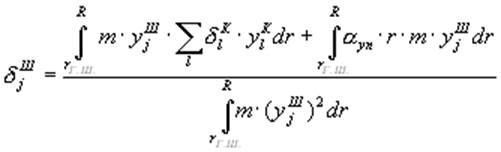 (13)
(13)
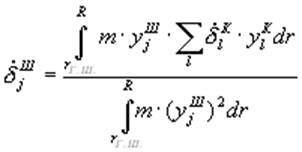 (14)
(14)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.