Об усталостной прочности лопасти несущего винта вертолета при действии ветровых нагрузок, страница 2

В момент касания ограничителя свеса, при опускании лопасти вниз, будем иметь

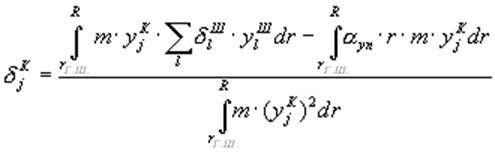 ,   (15)

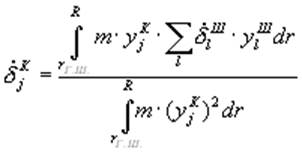 .   (16)

Таким образом, по формулам (13) и (14) вычисляются начальные условия при численном интегрировании уравнения (8) для момента времени, в который происходит изменение консольных собственных форм в решении (4) на шарнирные. Выражения (15) и (16) служат для вычисления начальных условий при обратной смене форм.

По описанной методике был проведен расчет деформаций и изгибающих моментов, действующих в лопасти несущего винта вертолета Ми-8 при штормовом ветре. Вертолет с невращающимся несущим винтом (угловая скорость вращения винта ) находится на стоянке и обдувается ветром. Направление ветра определяется азимутальным положением лопасти и углом наклона вектора скорости ветра к горизонту (рис.2). Скорость ветра изменяется во времени по заданному на рис.3 закону, который соответствует штормовому порыву . На графике (рис.4) в этом же масштабе времени показано изменение прогиба конца лопасти. Из графика видно, что реакция лопасти на порыв ветра представляет собой затухающий во времени колебательный процесс.

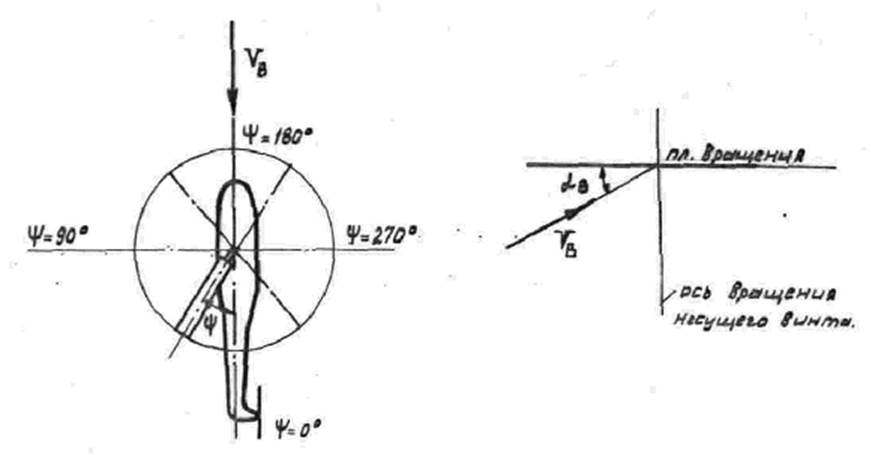
Рис. 2

Момент времени, соответствующий наибольшему отклонению конца лопасти, является расчетным. В это время имеют место максимальные деформации лопасти, а в лонжероне действуют наибольшие изгибающие моменты. Расчетным сечением для незашвартованной лопасти является сечение, находящееся на относительном радиусе . В этом сечении при изгибающем моменте равном , по результатам лабораторных испытаний, происходит потеря устойчивости нижней панели лонжерона.

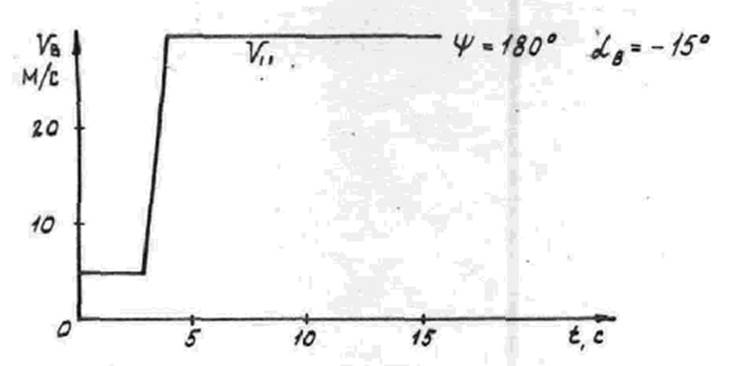
Рис. 3

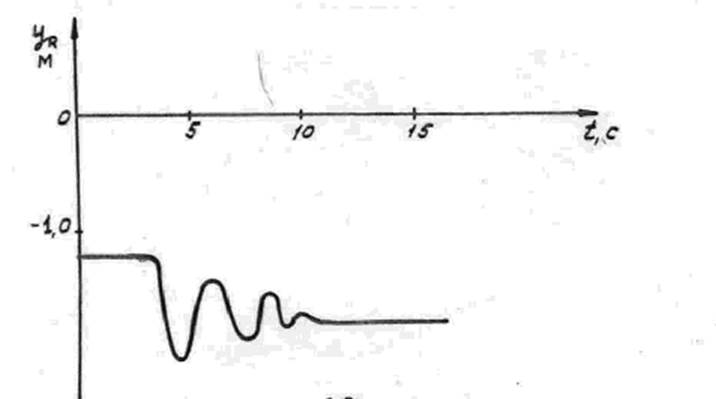
Рис. 4

Данную величину изгибающего момента будем считать расчетной. С целью определения азимута лопасти, на котором происходит наибольшая ее деформация, для заданного угла атаки винта () проводился расчет для углов (рис. 5). На рис. 6 представлен график максимальных изгибающих моментов в расчетный момент времени в функции азимута для того же значения угла атаки винта. Из этих двух графиков видно, что наибольший прогиб конца лопасти происходит тогда, когда лопасть находится на азимуте . На этом же азимуте действует и максимальный изгибающий момент. На рис. 7 показана форма упругой линии лопасти, полученная из этого расчета, которая соответствует моменту времени (через после начала действия порыва). В это время лопасть находится на упоре ограничителя свеса, и колебания происходят по консольным формам. На рис. 8 представлены графики прогиба конца лопасти, находящейся на азимуте , в функции угла атаки винта.

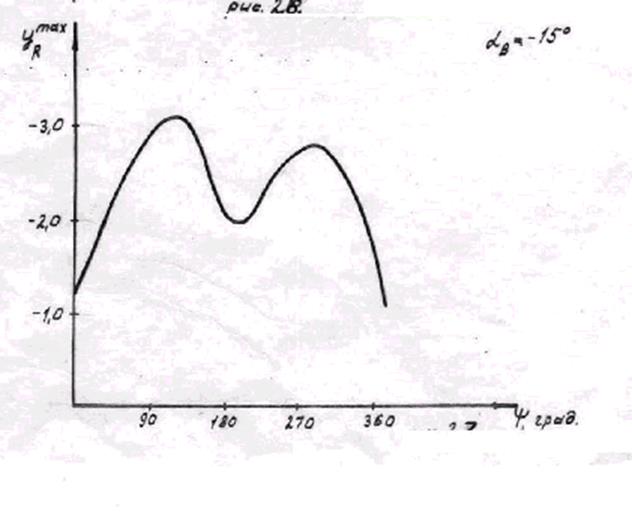
Рис.5

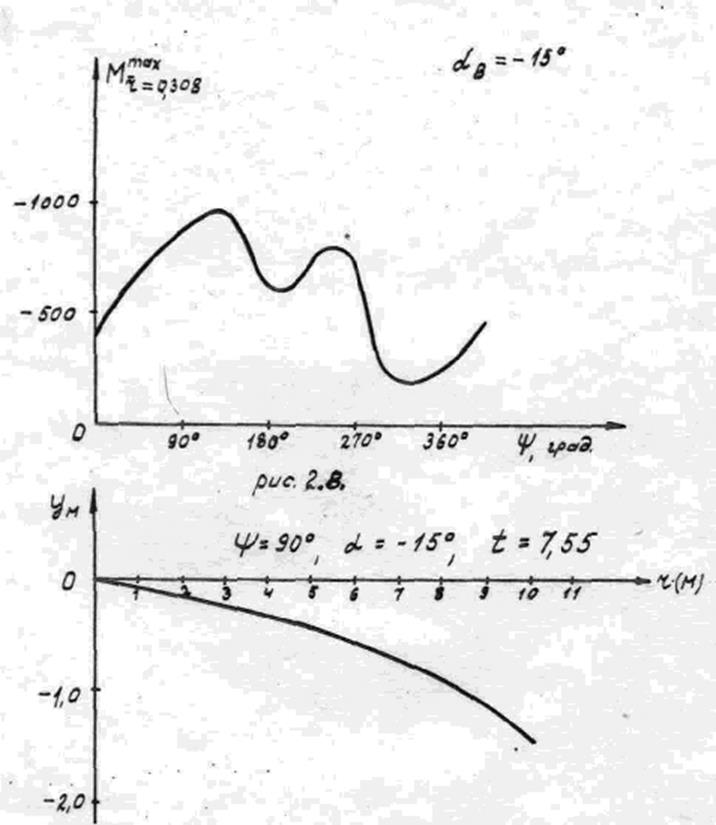
Рис. 7

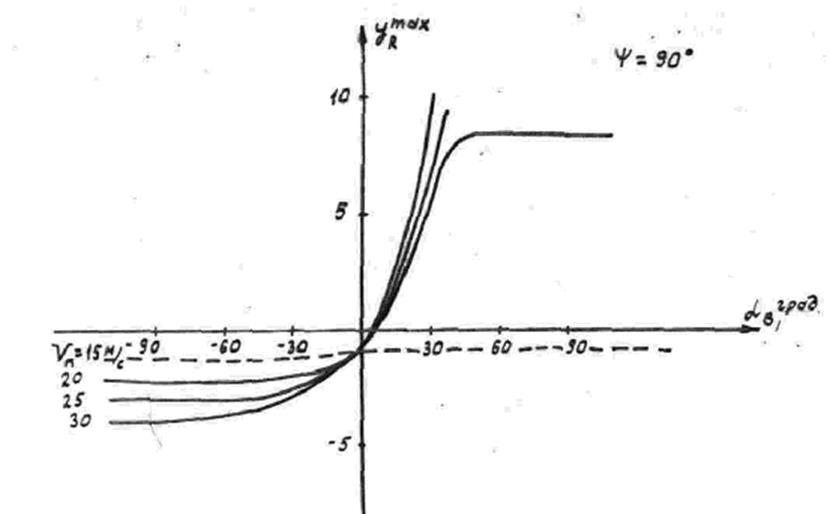
Рис. 8

Эти зависимости рассчитаны для порывов ветра разной интенсивности, когда скорость ветра нарастала по закону, представленному на графике рис. 3. Из графиков видно, что в зоне отрицательных углов атаки винта лопасть деформируется как консольно закрепленная в комле балка. Прогибы конца лопасти выходят на асимптоту, достигая максимальных величин при угле атаки винта, равном . Для отрицательных углов атаки, превосходящих по модулю 30⁰, лопасть достигает уровня колес вертолета при скоростях порыва ветра . При этой скорости ветра, но в области положительных углов атаки винта, лопасть будет заброшена вверх. Следует отметить, что в природе порывы ветра не постоянны по величине и направлению. К тому же втулка винта имеет ограничитель угла взмаха лопасти вверх, который не учтен в расчете. Поэтому представленные зависимости (особенно в области положительных углов атаки винта) и вытекающие из них ограничения следует рассматривать как взятые с запасом. На графиках рис. 9 представлены изгибающие моменты, действующие в расчетном сечении лопасти. Как видно из графиков, при скорости порывов ветра и угле атаки , изгибающий момент превышает величину, при которой нижняя панель лонжерона теряет устойчивость. В диапазоне положительных углов атаки винта изгибающий момент не велик, т.к. движение лопасти происходит по шарнирным формам. На рис. 10 показан график изменения напряжений в лонжероне лопасти в расчетном сечении для скорости порыва ветра .

Для оценки влияния швартовки был сделан расчет деформаций и изгибающих моментов зашвартованной лопасти. В расчетной схеме лопасть представлялась как двухопорная шарнирно-опертая балка (рис. 1г). По результатам расчетов можно сделать вывод, что во всем диапазоне углов атаки винта максимальный прогиб при не превышает по абсолютной величине . При этом максимальный изгибающий момент в точке максимального прогиба равен , что соответствует напряжению в лонжероне лопасти . Таким образом, для обеспечения прочности и сохранения перемещений незашвартованной лопасти в допустимых пределах во всем диапазоне углов атаки винта скорость ветра не должна превышать . Наиболее опасным азимутом при действии ветровых нагрузок является .

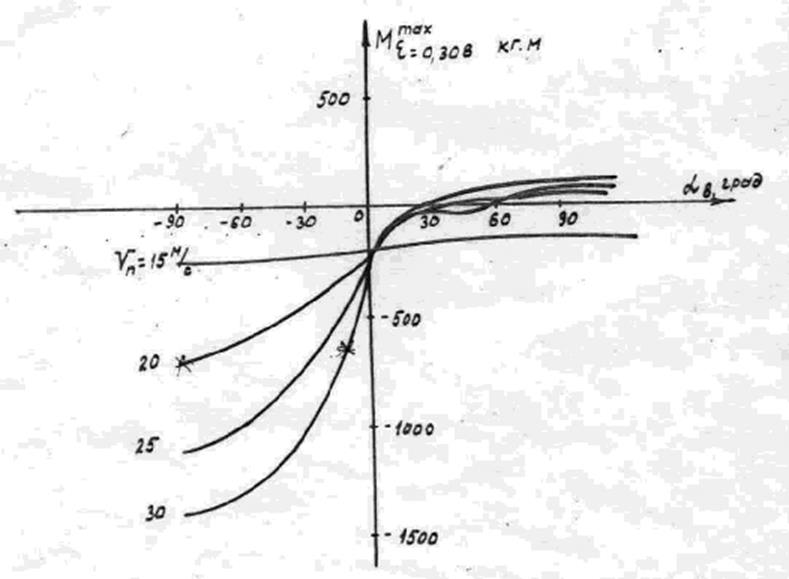
Рис. 9

Расчет зашвартованной лопасти проводился для швартовки, конструкция которой обеспечивает неподвижность ее конца. В этом случае упругие деформации лопасти и действующие в лонжероне изгибающие моменты находятся в допустимых пределах во всем диапазоне углов атаки винта до скорости ветра .

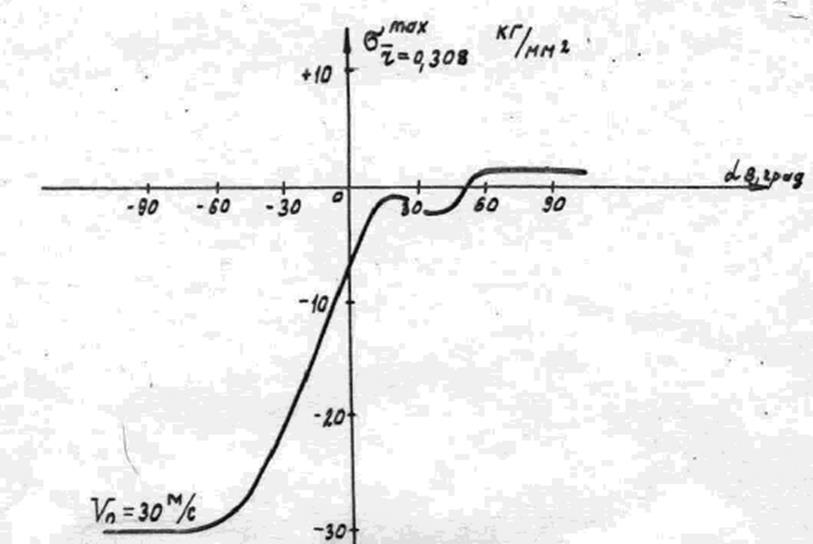
Рис. 10

Список литературы

1. Миль М.Л., Некрасов А.В., Браверман А.С., Гродно Л.Н., Лейканд М.А. Вертолеты. v М.: Машиностроение, 1967. - 424 с.

2. Михеев Р.А. Исследование динамической прочности лопастей несущего винта вертолета при горизонтальном полете и в неспокойном воздухе. / Р.А. Михеев, А.И Туркина А.И. Братухина] // Современные проблемы строительной механики и прочности летательных аппаратов. Всесоюзная конф., Москва. 1983: Тез. Докл. - МАИ, 1983. v c. 156.

________________________________________________________________________________________

сведения об авторе

Братухина Анна Ивановна, доцент кафедры строительной механики и прочности Московского государственного авиационного института (технического университета), к.т.н.

s