Файл 4
ЛПЗ №4 Розрахунок навантаження з'єднаного у ''трикутник".
Мета роботи: Оволодіти методиками розрахунку навантаження з'єднаного у ''трикутник".
4.1 Обсяг завдання
1.Відповідно до варіанта, вибраного на попередньому занятті, визначити лінійні і фазні струми споживачів і джерела розрахункової схеми.
2.Правильність обчислення струмів довести складанням балансу потужностей джерела та споживачів.
3.На комплексній площині побудувати векторні діаграми струмів та напруг окремих споживачів і джерела, з використанням яких проаналізувати характери навантажень у фазах споживачів.
4.2 Методичні вказівки до аналізу кола
За заданими значеннями індуктивностей Lфі ємностей Сф , аналогічно розрахунку кола однофазного струму, розраховують реактивні опори ХLф = 2πf. та ХCф =(2πfСф)-1, після чого записують комплекси повних опорів фаз (аb, bс, са) трикутника (Ом):
![]()
![]()
![]()
![]()
![]()
![]()
За законом Ома розраховують комплекси фазних струмів (А):
![]()
![]()
![]()
У разі з'єднання фаз споживача у „трикутник" комплекс лінійв го струму визначають як різницю комплексів відповідних фазіте струмів:
![]()
Для розрахункової схеми комплекси лінійних струмів будуть (А)
![]()
![]()
![]()
Правильність визначення комплексів струмів
„трикутника” перевіряють за першим законом Кірхгофа ![]() :
:
(44,79 - j1,36) + (-5,93 - j30,24) + (-38,87 - j31,6) ![]() (0 ± j0) .
(0 ± j0) .
У разі його невиконання треба перевіряти розрахунок напруг струмів з'єднання.
Комплекси повної потужності ![]() (ВА) активні Рф∆ (Вт) та
ре активні Qф∆
(вар) потужності фаз „трикутника", а також з'єднання І цілому відповідно
(ВА) активні Рф∆ (Вт) та
ре активні Qф∆
(вар) потужності фаз „трикутника", а також з'єднання І цілому відповідно ![]() , Р∆ , Q∆ визначають за такими формулами:
, Р∆ , Q∆ визначають за такими формулами:
![]()
S![]() =
=![]() SФ
SФ![]() =P
=P![]() j Q
j Q![]()
Для розрахункової схеми ці величини мають такі значення:
Sab = 10e jО * 382 = 14440е j0 = (14440 + j0);
Sbc = 13е -j67.37 * 29,232 = 11107е –j67.37 = (4272 – j10253);
Sca = 16.12e j29.74 • 23,572 = 8955е j29.74 = (7778 + 4444);
S![]() = (14440 +
j0) + (4272
-j10253) +
(7778 + І4444) = (26490-j5809).
= (14440 +
j0) + (4272
-j10253) +
(7778 + І4444) = (26490-j5809).
Зверніть увагу: оскільки за умовою розрахункової задачі до одного джерела підключені кілька споживачів ("зірка" і "трикутник"), то комплекс лінійного струму „трикутника'' не дорівнює комплексу відповідного фазного струму джерела і, отже, у цьому разі не можна визначати потужності фаз джерела і потужність джерела в цілому. Коли ж до джерела підключений лише один „трикутник" потужність джерела визначаємо за формулою:
Sф дж = Uф дж Iл![]() = Pф дж
= Pф дж ![]() jQф дж;
jQф дж;
Sдж = ![]() Sф дж = Pдж
Sф дж = Pдж ![]() jQдж.
jQдж.
За результатами розрахунків на комплексній площині будують суміщену діаграму струмів і напруг „трикутника” (рис. 3.6) у такому порядку:
1) у масштабі, аналогічному рис. 3.4.б, будують „зірку” векторів фазних (вана ж – „зірка" векторів лінійних)
напруг споживача (джерела);
2) з центра координат
площини у масштабі (Мі), з урахуванням напрямків (кутів) відкладають
вектори лінійних (ІА![]() , ІВ
, ІВ![]() , ІС
, ІС![]() ) і фазних (Іab , Ibc , Ica ) струмів
з’єднання;
) і фазних (Іab , Ibc , Ica ) струмів
з’єднання;
3) з кінців векторів Іab , Ibc , Ica , змінивши напрямок на зворотний , відкладають і показують
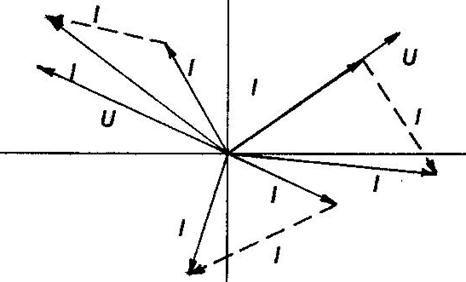
Рис 4.1
пунктирно вектори відповідно: – Іca , Іab , Іbc .
4) на діаграмі показують
кути зсуву фаз ![]() у фазах „трикутника"
(кути між фазним струмом (Іab , Іbc
, Іca)і відповідною фазах з напругою споживача).
у фазах „трикутника"
(кути між фазним струмом (Іab , Іbc
, Іca)і відповідною фазах з напругою споживача).
За правильно виконаних розрахунків струмів і правильно довжини їх векторів на діаграмі отримують три трикутники струми однією стороною кожного з цих трикутників є вектор лінійного струму. Дві інші сторони кожного з трикутників утворені векторами однакових струмів, один з яких має зворотний напрямок і поданий пунктиром.
З аналізу векторної діаграми випливає споживача з’єднаного в „трикутник” мають навантаження :
ФАЗА ab — активне, оскільки кут зсуву дорівнює нулю:
![]() ab =
ab = ![]() uab –
uab – ![]() I ab = 300 – 300 =00 ;
I ab = 300 – 300 =00 ;
ФАЗА Ьс — активно-ємнісне, оскільки кут зсуву фаз від’ємний:
![]() bc =
bc = ![]() u bc –
u bc – ![]() I bc = -900 – (-22,620) = –67,38° <00;
I bc = -900 – (-22,620) = –67,38° <00;
ФАЗА са — активно - індуктивне, оскільки кут зсуву фаз від’ємний:
![]() ca =
ca = ![]() u ca –
u ca – ![]() I ca = 1500– 120,260 = 29,710 > 00.
I ca = 1500– 120,260 = 29,710 > 00.
Зверніть увагу: за правильно виконаних розрахунків та правильно побудованої діаграми кут між вектором фазного струму і вектором відповідної фазної напруги споживача (кут зсуву фаз ) дорівнює комплексу повного опору цієї фази.
4.3 Розрахунок балансу потужностей схеми.
Оскільки до одного джерела підключені два споживачі („зірка" і „трикутник") то комплекс повної потужності Scп (ВА), активну Рсп (Вт) та реактивну Qcп (вар) потужності фаз і навантаження в цілому можна визначити так:
Scn = Sy +S![]() = Pcn
= Pcn![]() jQcn
= 6517-j4912+26490-j5809 = 33007-j10720 = 34704e-j17,99
jQcn
= 6517-j4912+26490-j5809 = 33007-j10720 = 34704e-j17,99
Комплекс повної потужності Sф дж(ВА),активну Pф дж(Вт) та активну Qф дж(вар) потужності фаз джерела , а також джерела в цілому Sдж(ВА) розраховують за формулою:
Sф дж = Uф дж Iф дж = Pф дж ![]() jQф дж;
jQф дж;
Sдж = ![]() Sф дж = Pдж
Sф дж = Pдж![]() jQдж
jQдж
Для розрахункової схеми ці величини дорівнюють:
SA = UAIA =220еj0*57.9ej10.51 = 12738ej10.53 = (12523+j2328);
SВ = UBIB = 220е-j120*49.25ej70.71 = 10835e-j49.29 = (7067-j8213);
SC = UCIC = 220ej120*65.2e-j139.67 = 14344e-j19.67 = (13507-j4828);
Sдж = 12523+j2328+ 7067- j8213 +13507- j4828=33097-j10713 = 34788e-j17.94
Похибку розрахунку трифазного кола оцінюють за такою самою методикою, як і для кола однофазного змінного струму:
![]() =
100 (Рсп - Рдж) / Рдж =(33007 - 33097) / 33097 = -0,27%;
=
100 (Рсп - Рдж) / Рдж =(33007 - 33097) / 33097 = -0,27%;
![]() = 100(Qсп -Qдж)/Qдж = (-10720-(-10713)) / (-10713) = 0,065%.
= 100(Qсп -Qдж)/Qдж = (-10720-(-10713)) / (-10713) = 0,065%.
При ![]() < ±1 % та
< ±1 % та
![]() <
< ![]() 1
% задача розв'язана правильно.
1
% задача розв'язана правильно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.