





Файл 4
Перехідні процеси в електричних колах
1. Приклади аналізу перехідних процесів:
1.1. Вмикання котушки індуктивності до джерела постійної ЕРС.
1.2. Вмикання конденсатора до джерела постійної ЕРС (через резистор)
1.3. Відключення котушки індуктивності від джерела постійної ЕРС з розрядом на резистор.
1.4. Відключення конденсатора від джерела постійної ЕРС з розрядом на резистор.
1.5. Підключення котушки індуктивності до джерела синусоїдної ЕРС.
1.6. Розряд конденсатора на котушку індуктивності.
1. Приклади аналізу перехідних процесів
1.1. Вмикання котушки індуктивності до джерела постійної ЕРС
Вважається, що параметри схеми заміщення R, L котушки індуктивності і постійна ЕРС Е задані.
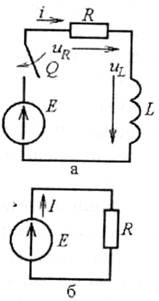
Рис. 5.4
У відповідності до загальних правил складаємо рівняння за другим законом Кірхгофа для кола після замикання вимикача Q, а саме uR + uL = Е, де напруги виразимо за (5.4) через струм і:
![]()
Розв'язання шукаємо для струму у вигляді суми двох складових і = іy + iв.
ЕРС постійна, тому усталений струм буде також постійним, і його можна визначити за схемою рис. 5.4, б, отриманої зі схеми рис. 5.4, а, а саме
![]()
(для постійного струму елемент L не чинить опору).
Для вільної складової при Е = 0 з (5.10) маємо диференційне рівняння першого порядку:
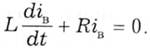
Його розв'язання відоме з курсу математики і має загальний вигляд (5.9) iв = Аіерt, де Аі – стала інтегрування, р - характеристичний параметр, е - основа натуральних логарифмів.
Для знаходження р визначимо похідну
![]()
і підставимо її в Тоді з Lрів + Riв = 0 маємо характеристичний параметр
![]()
На практиці використовується величина
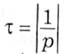
постійна часу [с], яка задає швидкість протікання перехідного процесу і його тривалість.
Конкретно для кола, що розглядається:
![]()
Зводимо усталену і вільну складові разом (5.8):
![]()
До комутації при t = -0 струм у колі відсутній: i(-0) = 0. За першим законом комутації (5.1) після замикання вимикача в колі за рис. 5.4, а струм повинен зберегтися: i(+0) = i(-0). Таким чином початкове значення струму i(0) = 0 , тобто і = 0 при t = 0. Після підстановки цих значень у формулу (5.13) маємо
![]()
а звідси - і саму сталу інтегрування
![]()
З урахуванням цього підсумкові розв'язки для струму (5.13), а також для напруг на елементах L і R:
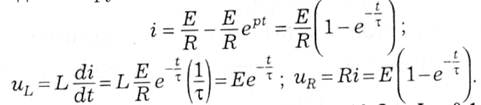
1.2. Вмикання конденсатора доджерелапостійної ЕРС(через резистор)
Вихідне рівняння для контура після комутації за другим законом Кірхгофа uR+uс = Е.
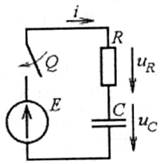
Рис. 5.6
Робимо підстановку за (5.4) і (5.6)
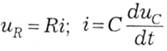
і отримуємо диференційне рівняння
![]()
яке за (5.8) підлягає розв'язанню у вигляді uс = ucу + ucв.
Очевидно, що всі усталені величини повинні бути постійними, тому що ЕРС постійна. У тому числі, усталена напруга конденсатора також є постійною величиною uСу = Uс = Е (конденсатор зарядиться до напруги, яка дорівнює ЕРС джерела).
Рівняння для вільної складової при Е = 0 з (5.15) має вигляд:
![]()
а його загальний розв'язок за (5.9): uСB = Аuерt. Від цього виразу похідна
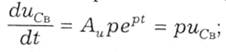
підставимо її у рівняння (5.16) і отримуємо RCpuCв + иСв = 0. Звідси знаходимо характеристичний параметр і сталу часу [с]:
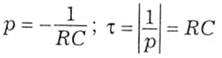
Зводимо розв'язки для двох складових воєдино:
![]()
вважаємо, що конденсатор був незаряджений, тому при t = 0 буде за законом комутації (5.2) uс(0) = 0 і після підстановки цього в (5.18) маємо Е+Аu = 0, звідки стала інтегрування Аu = -Е. Підсумковий розв'язок:
![]()
на основі чого з формули (5.6) маємо струм:
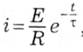
а потім і напругу на резисторі:
![]()
1.3. Відключення котушки індуктивності від джерела постійної ЕРС з розрядом на резистор
Діючи відповідно зі встановленим порядком, отримуємо наступні розрахункові вирази для схеми кола, що створилося після одночасної комутації вимикачів Q1 і Q2:
![]()
Розв'язок містить тільки вільну складову і = іВ, бо усталена складова і = 0 (в колі після комутації джерело відключене). Рівняння для вільної складової за (5.22):
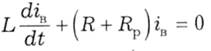
має відомий розв'язок (5.9) ів = Aіept.
За вже відомими діями визначаються характеристичний параметр і стала часу:
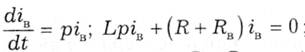
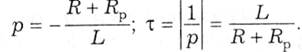
Для визначення сталої інтегрування Аі використаємо початкові умови. Коли вимикач Q1 був замкнений, від джерела через котушку індуктивності проходив постійний струм, але індуктивний елемент L при такому струмі не враховується, тому при t = 0 i(0) = E/R. Підставимо це у вираз струму iв і отримуємо рівняння
![]()
та сталу інтегрування
![]()
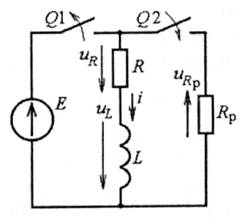
Рис. 5.8
Таким чином, розв'язки для струму і напруг:
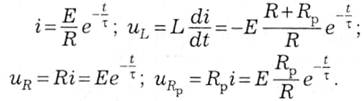
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.