Підсумковий розв'язок uc=uCy+uCB, який звичайно (5.8) утворюється зі складових, у даному випадку матиме тільки вільну складову uс = uСв, через те, що усталена складова uСу дорівнює нулю uСу = 0 у зв'язку з відсутністю первинного джерела електроенергії в розрядному контурі.
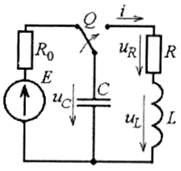
Рис. 5.15
Розв'язок диференційного рівняння (5.35) має загальну форму (5.9) у вигляді експоненти uc = Auept де Аu - стала інтегрування, е - основа натурального логарифма, р - характеристичний параметр. З метою визначення р візьмемо першу і другу похідні від
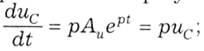
і підставимо їх у
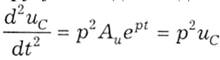
диференційне рівняння (5.35). Із виразу
![]()
який утворився, отримаємо характеристичне рівняння:
![]()
- це за суттю квадратне алгебраїчне рівняння.
Відомий розв'язок цього рівняння, який містить два кореня:
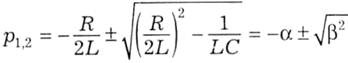
де позначено:
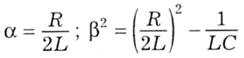
У залежності від значення підкореневого виразу β2 можливі три варіанти конкретних розв'язків, відомих із курсу математики.
Варіант 1. Якщо в (5.38) β2>0, то корені (5.37) дійсні, негативні і різні: р1=-α-β, р2=-α+β, причому р1<0; р2<0; |р1|>|р2|.
У цьому випадку розв'язок для напруги має вигляд:
![]()
а звідси і струм:
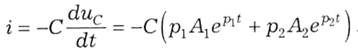
Сталі інтегрування А1 і А2 знайдемо, використовуючи початкові умови при і=0 за законами комутації (5.1) і (5.2): для струму i(0)=0 (у зв'язку з наявністю індуктивного елемента і за умови, що до комутації струм у ньому відсутній) і для напруги uс(0)=Е (у зв'язку з наявністю ємнісного елемента і за умови, що конденсатор був повністю заряджений від джерела). Початкові значення і і uс та значення t=0 підставимо у вирази напруги (5.39) і струму (5.40) та отримуємо систему з двох рівнянь:
![]()
Її розв'язання і дає сталі інтегрування:
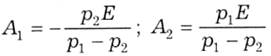
У підсумку стають повністю визначеними наведені вище функції напруги uс (5.39) і струму і (5.40). З урахуванням проміжних виразів функція струму може бути приведена до вигляду:
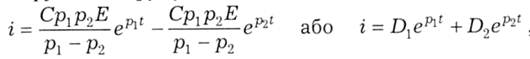
причому D1<0 ; D2>0 і |D1| = |D2|.
Варіант 2. Якщо за формулою (5.38) β2<0, то хай β2 = (-1)х
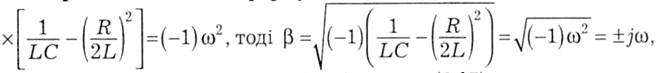
а характеристичне рівняння (5.36) має за (5.37) два комплексно спряжених кореня: р12 =-α±jω, де дійсна частина (-α) негативна (α - коефіцієнт згасання), тобто:
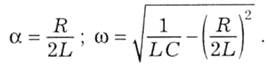
У цьому випадку розв'язок для напруги має вигляд:
![]()
і задача полягає у визначенні сталих інтегрування Аu і γu.
Варіант 3. Якщо за формулою (5.38) β2=0, то замість (5.37) маємо два однакових дійсних негативних кореня
![]()
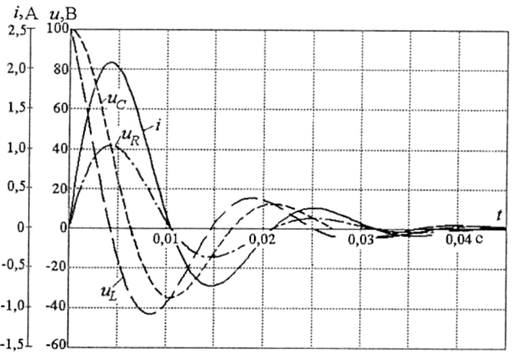
Рис. 5.17
У цьому випадку розв'язок для напруги має вигляд:
![]()
а звідси і струм:
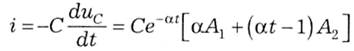
Використовуючи вже відомі початкові умови при t=0: uс=Е; i=0 і підставивши їх у вирази напруги (5.48) і струму (5.49), отримаємо сталі інтегрування:
А2=Е; А2=αА1=αЕ.
Типові графіки функцій струму і і напруги uс подано на рис. 5.18 у безрозмірній формі.
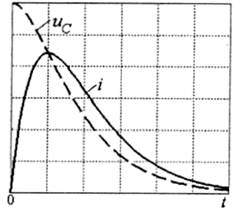
Рис. 5.18
Література
1. Овчаров В.В. Теоретичні основи електротехніки К.: Урожай, 1993 р.
2. Иванов И.И. Равдоник В.С. Электротехника. Учебное пособие для неэлектрических специальностей вузов. - М.: Высшая школа . 1984. - 375 с.
3. Клауснитцер Г. Введение в электротехнику. Пер. нем. - М: Энергоатомиздат. 1985. - 480 с.
4. Яцкевич В.В. Электротехика. Учебное пособие.- Минск: Урожай. 981.-183 с.
5. Богуславский В.А., Калымаков В.И., Деметицкая Т.Д. Методические указания к лабораторным работам по теоретическим основам электротехники. Раздел “Электрические цепи постоянного тока” - часть., Харьков, ХАДИ, 1991. - 24 с.
6. Прищеп В.Г. Электротехніка. Методические указания по изучению дисциплины и задание для контрольной работы студентам - заочникам сельскохозяйственных вузов по специальности 1509 - “Механизация сельского хозяйства”. - М.: ВСХИЗО. 1987. 37 с.
7. Общая электротехника с основами электроники. Учебник для техникумов / В.А. Гаврилюк, Б.С. Гершунский, А.В. Ковальчук, Ю.А. Куницкий, А.Г. Шаповаленко – Киев: Вища школа. Головное издательство. 1980. – 480 с.
8. Л.А. Бессонов. Теоретические основы электротехники. Издание четвертое. Москва: Высшая школа. 1964. – 750 с.
9. Электротехніка. Учебник для неэлектрических специальностей. Под ред. В.Г. Герасимова - М.: Высшая школа, 1985. - 480 с.
10. Борисов Ю.М. и др. Электротехника. Учебник для вузов - М.: Энергоатомиздат. 1985. - 522 с.
11. О.М. Кобяков, М.М. Ляпа, В.М. Лисенко, В.І. Грабчак, В.В. Гриненко: Аналогова схемотехніка Навчальний посібник. – Суми. Видавництво Сум.ДУ, 2007. – 209 с.
12. Братущак М.П. Методичні вказівки по виконанню контрольної роботи з “Електротехніки”. Суми, 1997 рік.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.