1.4. Відключення конденсатора від джерела постійної ЕРСз розрядом на резистор
Припустимо, що конденсатор був заряджений від джерела постійної ЕРС Е. Потім вимикачем Q1 відключили джерело і замкнули вимикач Q2, ініціюючи тим самим перехідний процес розряду конденсатора.
Для контура, що залишився, за другим законом Кірхгофа складемо рівняння:
-uс + uR + uRр = 0.
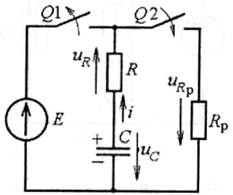
Рис. 5.10
Зробимо підстановки UR = Ri
![]()
у це рівняння й отримаємо проміжний вираз
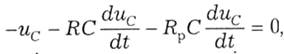
а після спрощень маємо диференційне рівняння з одним невідомим uс:
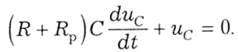
Розв'яжемо рівняння (5.25) звичайним чином. Усталена складова uСу = 0 (при досягненні усталеного стану конденсатор повністю розрядиться). Тому підсумковий розв'язок складається тільки з вільної складової uс = uСв і має відомий загальний вигляд uс = Аuерt. Діючи, як і в пункті 5.3.2, беремо похідну від uс і формуємо характеристичне рівняння (R + Rр)Срuс + uс = 0. Знаходимо його корінь і сталу часу для кола, що розглядається:
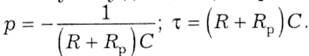
У відповідності з другим законом комутації (5.2) напруга на ємнісному елементі миттєво змінитися не може, тобто при L=0 маємо uс = Е. Підставляючи це у формулу розв'язку, маємо Е = Аuер0, звідки отримаємо сталу інтегрування Аu=Е і підсумковий розв'язок:
![]()
На його основі струм
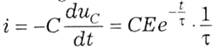
остаточно:
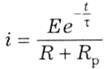
1.5. Підключення котушки індуктивності до джереласинусоїдної ЕРС
Джерело має синусоїдну ЕРС е = Еmsin(ωt + ψе).
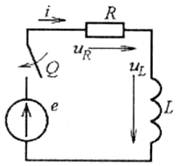
Рис. 5.12
Для кола за рис. 5.12 після його комутації рівняння має вигляд uL + uR = е. Але з урахуванням (5.4) отримуємо диференційне рівняння:
![]()
розв'язок якого і = іy + ів складається з двох складових струму.
ЕРС синусоїдна, тому всі усталені електричні величини також будуть синусоїдними, в тому числі і струм:
![]()
Цю функцію усталеного струму належить визначити за правилами розрахунку кіл синусоїдного струму. А саме, індуктивний і повний опори кола, амплітуда струму, фазовий зсув між струмом і ЕРС та початкова фаза струму визначаються за відомими формулами:
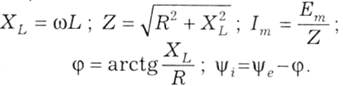
Рівняння для вільної складової відповідає розглянутому в прикладі 5.3.1 і має вигляд (5.11)
![]()
Воно розв'язується за відомими вже правилами, тобто вільна складова струму
![]()
а відповідний характеристичний параметр і стала часу (5.12) мають вже відомі вирази
![]()
Зводимо складові струму разом і маємо для нього розв'язок
![]()
Сталу інтегрування А1 знайдемо, використовуючи початкові умови і перший закон комутації (5.1), тобто i(0) = 0. Підставляючи це і L = 0 у вираз струму (5.32), маємо
![]()
а звідси
![]()
Остаточний вираз для струму:
![]()
Тут можливі два крайні випадки отриманої функції, які ми розглянемо на конкретному прикладі при наступних вихідних даних для схеми за рис. 5.12:
L = 0,1 Гн; R = 5 Ом; Ет = 180 В; ω = 314 с-1.
За формулами (5.31) і (5.12) знаходяться:
ХL = 31,4 Ом; Z = 31,8 Ом; Іт = 5,66 А; φ = 81°; т = 0,02 с.
Перший - простіший - варіант функції струму отримуємо при ψі = 0, що можливо, якщо ψе = φ = 81°. Тоді відразу маємо усталений синусоїдний процес (5.30) і = Іт sinωt = 5,66sin314t А. Відповідні графіки для ЕРС і струму подані на рис. 5.13.
Другий - найбільш складний варіант - отримуємо при ψi=π/2=90°, що можливо, якщо ψе=ψi+φ=90°+81°=171°=2,985 рад.
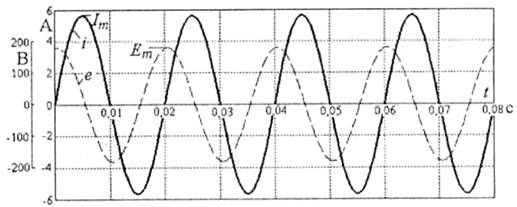
Рис. 5.13
У цьому випадку маємо за (5.33) функцію струму
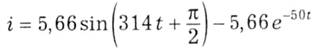
Графік цієї функції разом з графіками ЕРС і усталеної та вільної складових струму подані на рис. 5.14.
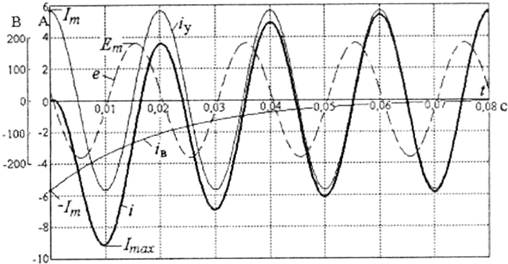
Рис. 5.14
Очевидно, що найбільше значення струму виникає протягом першого періоду і в цьому випадку це екстремальне значення Іmах = 9,12 А, а взагалі існує обмеження Imах < 2Iт.
При інших значеннях функція струму має проміжний вигляд між двома крайніми випадками, поданими на рис. 5.13 і 5.14.
1.6. Розряд конденсаторана котушку індуктивності
Як випливає зі схеми заміщення на рис. 5.15, конденсатор С був попередньо заряджений від джерела постійної ЕРС Е, а потім переключений на котушку індуктивності, що подана резистивним R і індуктивним L ідеальними елементами.
Щоб розрахувати перехідний процес, розглянемо контур, що утворився після комутації кола перемикачем Q. Для цього контура за другим законом Кірхгофа складаємо рівняння:
uL+ uR - uc = 0.
Для того, щоб залишити одне невідоме, а у даному випадку це буде напруга на конденсаторі uс, врахуємо відомі взаємозв'язки величин (5.4), (5.6)
![]()
(знак мінус через зустрічні напрямки uс та i), і отримуємо диференційне рівняння другого порядку
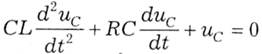
яке подамо у вигляді:
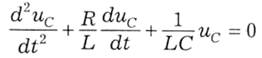
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.