Трифазні асинхронні двигуни, страница 4

де,  з   урахуванням   відомого   для   синусоїд   співвідношення

і з урахуванням (14.11), амплітуда магнітної індукції

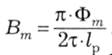
Нехай система координат на рис. 14.15 разом із кривою В^х) рухається зі швидкістю У_ь що відповідає частоті обертання п_х.

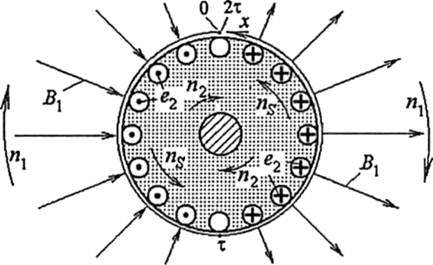
Рис. 14.14

Туди ж зі швидкістю У₂, що відповідає частоті обертання ротора п₂, рухаються провідники його обмотки. Тоді від­носно осі х ці про­відники переміщу­ються з відносною швидкістю У₅, що відповідає частоті ковзання S (14.8). З урахуванням (14.8), (14.1), (14.9) і (14.10), ця швидкість.

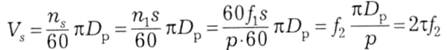
Будемо вважати, що на рис. 14.15 зображено миттєве поло­ження провідників для моменту часу t=0. Тоді з плином часу про­відники змінюють своє розташування відносно осі х. І для провідника к з початковим положенням

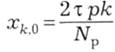
де N_р – кількість провідників обмотки ротора, отримується поточна координата

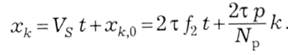
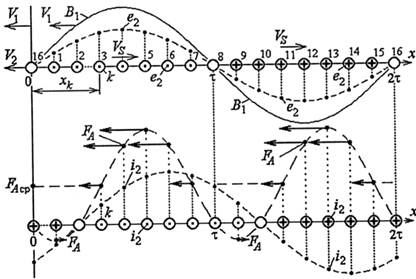
Рис. 14.15

З урахуванням переміщення провідників відносно хвиль кривої В₁(х), можна записати миттєві значення магнітної індукції для провід­ника з номером к як функцію часу, підставивши (14.15) в (14.12), а саме:

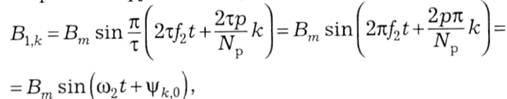
де ω₂=2πf₂ - кутова частота;

За (14.2) в /с-тому провіднику ротора миттєве значення ЕРС

є синусоїдною функцією часу з частотою f₂ і амплітудою S_2m=2T/₂Z_pB_m.

Відповідний розподіл миттєвих значень ЕРС е₂ по всіх провід­никах показано на рис. 14.15 точками. Обвідна крива е₂(х) просто­рово подібна до кривої В^х) і вони рухаються синхронно.

В інших провідниках обмотки ротора все буде аналогічно, але з певним часовим зсувом. І під дією ЕРС е₂ в кожному провіднику короткозамкненого ротора виникає синусоїдний струм

де амплітуда струму і його фазовий зсув відносно ЕРС е₂ визна­чаються з використанням активного R₂ й індуктивного Х₂ опо­рів фази обмотки ротора за звичайними правилами розра­хунку кіл синусоїдного струму:

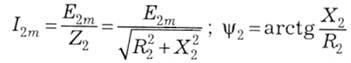
Для ілюстрації припустимо. Такому фазовому зсуву на рис. 14.15 буде відповідати просторовий зсув (відставання) струму г₂ від ЕРС е₂ на т/4. Відповідний розподіл миттєвих значень струмів і₂ по провідниках показано в нижній частині рис. 14.15.

Підставимо (14.16) і (14.18) у формулу (14.3) й отримаємо силу, що діє на fc-тий провідник ротора

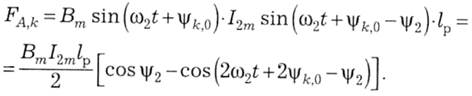
Миттєвий розподіл сил по провідниках при t=0 показано на рис. 14.15 у взаємозв'язку з розподілами B_v e₂ i i₂.

За період T₂ =-j- зміни цих величин середнє значення сили для fc-того провідника

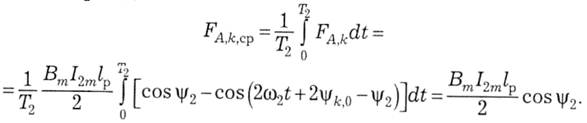
Це середнє значення сили за період дає середнє значення моменту обертання для одного провідника

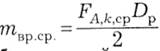
А з урахуванням усіх провідників отримуємо обертальний електро­магнітний момент, що діє на ротор,

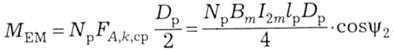
Якщо підставити в_т за (14.13) і виразити амплітуду струму через його діюче значення і₂, то з урахуванням (14.10)

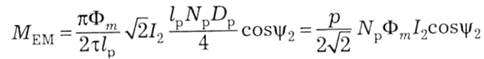
Параметри ТАД в (14.23) виразимо коефіцієнтом

і подамо електромагнітний момент у формі

Тут у явному вигляді залишились величини Ф_т, І₂, ψ₂, які можуть змінюватися в процесі роботи ТАД. Ця формула нагадує формулу елек­тромагнітного моменту МПС (13.14), але з суттєвим додатком cosψ₂, поро­дженого специфікою машини змін­ного струму.

Формула (14.24) явно показує, що електромагнітний момент ТАД породжений взаємодією магнітного поля, збудженого обмоткою ста­тора, і струму ротора. Але, на від­міну від МПС, струм у ротор не треба підводити через щітки і колектор - він індукується обер­товим магнітним полем. Це і стало суттєвою перевагою ТАД над ДПС

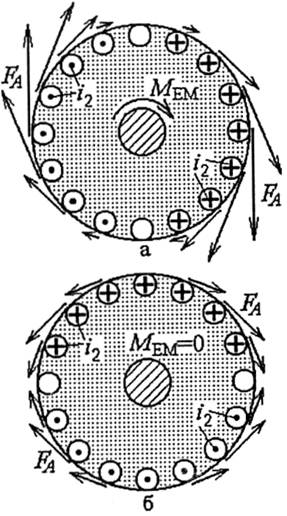
Рис. 14.16

Вплив фазового зсуву щ (14.19) на М_ЕМ (14.24) показанонарис. 14.16 розподілом сил F_Ak по провідниках ротора для двох крайніх випадків. При R₂>Х₂ за (14.19) ψ₂>0 і всі сили F_A за (14.20) діють погоджено, створюючи найбільше значення М_ЕМ (рис. 14.16, а). При R₂<Х₂ отримується ψ₂→π/2 і за (14.20) створюється баланс позитивних і негативних значень сил Е_А, а сумарний М_ЕМ=0 (рис. 14.16, б).

Формула М_ЕМ (14.24) й інші формули отримані в припущенні короткозамкненої обмотки ротора. Проте вираз (14.24) справедли­вий і для обмотки фазного ротора, тільки за (14.17) і (14.18) будуть отримані ЕРС і струм однієї фазної обмотки з урахуванням всіх ьо₂ її витків, а в (14.19) треба використовувати опори не одного про­відника, а знову ж таки, всієї фазної обмотки.

Так, наприклад, для фазного ротора амплітуда ЕРС