Трифазні асинхронні двигуни, страница 3

де смисл складових той же, як і у ДПС (13.19).

Очевидно, що електромагнітний момент, як і сили спрямовані в той же бік, куди первісно обертається магнітне поле. Тому в той же бік обертається і ротор. Усталене значення частоти обер­тання п₂ досягається при М = М_с, де М_с - гальмовий момент опору, який діє на вал ротора з боку механічного навантаження.

В асинхронних двигунах виявляється п₂<п₁, тобто ротор обертається повільніше, ніж магнітне поле. Вони обертаються асин­хронно, що і послужило основою для назви таких двигунів.

Дійсно, із наближенням п₂ до п₁ відносна швидкість провідни­ків V_s зменшується, ЕРС е₂ (14.2) також зменшується, отже змен­шуються струми і₂, сили Ампера (14.3) й електромагнітний момент М_ЕМ. І якщо припустити, що п₂ = п₁, то названі величини стануть нульовими, під дією М_с і внутрішнього гальмуючого моменту ΔМ ротор сповільнює хід і відновиться неминуча умова п₂<п₁.

Відставання ротора від обертового поля характеризується без­розмірною величиною s, що називається ковзанням і визнача­ється відношенням:

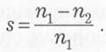
Із формули отримується частота обертання ротора:

що графічно проілюстровано на рис. 14.13.

При вмиканні ТАД магнітне поле практично миттєво починає обертатися з частотою п_1; а в ротора через механічнуї інерцію первісно буде п₂ = 0. Тому при пуску ТАД за (14.5) отримуємо в = 1. У міру розгону ротора вели­чина п₂ наближається до п₁ і при п₂→п₁ маємо s→0.

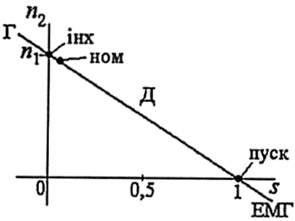
Рис. 14.13

Таким чином, у двигунному режимі асинхронна машина харак­теризується  діапазоном 0<s<1, що відображено на рис. 14.13 ділянкою «Д». Точка, що відповідає щ, є точкою «інх» - ідеального неробочого ходу, оскільки при М_с=0 відповідає ідеальній умові ΔМ=0. Точка «пуск» при s=1 - пускова. Номінальному режимові «ном» в ТАД відповідають достатньо малі ковзання S_Н0М=0,02...0,08. Тому номінальні частоти обертання ТАД

виявляються близькими (знизу) до встановленого ряду значень n₁ (див. табл. 12.1).

Якщо, за певних умов, має місце я<0, то ТАД переходить у рекупе­ративний генераторний режим (ділянка «Г» на рис. 14.13), при s>1 - в режим електромагнітного гальма (ділянка «ЕМГ»). Ці режими, в принципи, відповідають аналогічним режимам ДПС (див. підрозділ. 13.9.8).

Магнітне поле обертається відносно статора з частотою п₁ (14.1) і їй відповідає частота напруги і струму статора Д. Магнітне поле відносно ротора обертається з частотою ковзання

якій буде відповідати частота ЕРС і струмів ротора І₂. Щоб визначити цю частоту, складемо пропорцію

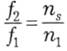
з якої отримуємо

тобто в робочому режимі ТАД частота електричних величин у роторі суттєво менше, ніж у статорі.

4. Електромагнітний момент у ТАД

Виходячи із принципу дії ТАД, виведемо математичний вираз його електромагнітного моменту. І оскільки все за (14.2) і (14.3) виникає за сприяння магнітного поля (див. рис. 14.12), то з нього і почнемо.

На рис. 14.12 розглянемо в обмотці ротора контури, створені діаметрально розташованими її провідниками. Тоді з контуром, площина якого перпендикулярна силовим лініям магнітного поля, зчеплений максимальний потік Ф_т, а для контура, площина якого паралельна силовим лініям, потік Ф=0. Відносно поля ротор пере­міщується з частотою обертання n₅ (14.8), тому у всіх контурах магнітний потік змінюється від -Ф_т до +Ф_т з частотою f₂ (14.9).

На рис. 14.12 магнітне поле має одну пару полюсів: під полюсом N силові лінії входять у ротор (це будемо вважати їхнім позитив­ним напрямком), під полюсом 5 виходять (негативний напрямок).

У загальному випадку за наявності р пар полюсів величина

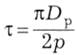
називається полюсним поділом - це довжина дуги окружності на діаметрі поверхні ротора Б_р, що припадає на один полюс.

Тоді середнє значення магнітної індукції на поверхні ротора, виходячи з формули (8.3),

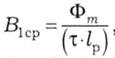
а конкретний розподіл магнітної індукції на поверхні ротора пока­зано на рис. 14.14 векторами В_г. Щоб показати це графічно, роз­горнемо кругову лінію поверхні ротора в пряму лінію, її початок візьмемо в точці 0, а напрямок задамо координатою х проти руху стрілок годинника.

Розподіл магнітної індукції В^х) уздовж лінії х на її довжині 2т зображено на рис. 14.15. Ця функція в ТАД вважається синусоїд­ною і її в даному випадку можна записати так