ТЕНЗОРЫ
ДСК = декартова с.к. ![]()
ЦСК = цилиндрическая с.к. ![]()
ССК = сферическая с.к. ![]()
ПСК = полярная с.к. ![]()
Вспомогательные формулы
Т1.
базис
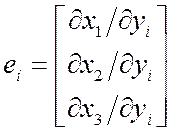
кобазис: 2 варианта
1) есть формулы ![]() Þ
Þ 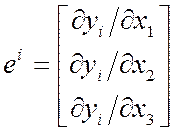
2) нет формул ![]() Þ
Þ ![]() Þ находим направления
Þ находим направления
![]() Þ нормируем векторы
Þ нормируем векторы ![]()
Т2.
разложение тензора ![]() ,
, ![]()
Т3.
метрический тензор ![]() … Þ симметричный
… Þ симметричный ![]()
Т4.
жонглирование индексами ![]()
Д1.
ковариантная производная 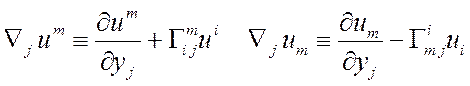
Д2.
символы Кристоффеля 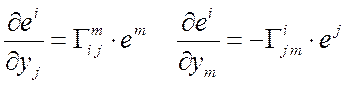 , см. 7
, см. 7
Д3.
градиент скалярной функции
Ñf = вектор 
Д4.
градиент векторной функции
![]() = тензор
= тензор ![]()
Д5.
дивергенция векторной
функции div F
=  = вектор, след матрицы
= вектор, след матрицы ![]()
Д6. дивергенция тензора (div T) ·u ≡ div (T*u)
1.
Найти базис, кобазис для ССК
ЦСК, базис из формул Т1 Þ 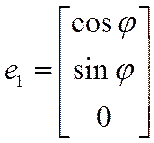
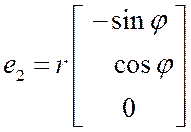
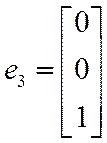
ЦСК, кобазис из формул Т1 вариант 2 Þ ![]()
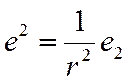
![]()
ДОМАШНЕЕ ЗАДАНИЕ: Найти базис, кобазис для ССК
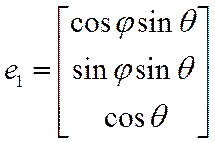
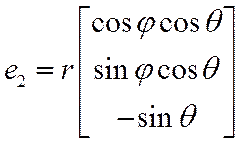
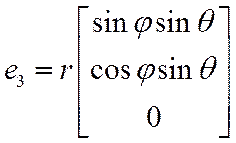
![]()
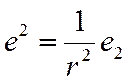
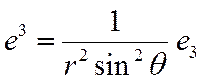
2.
Доказать: ![]()
столбцы ![]() =
векторы базиса: столбцы
=
векторы базиса: столбцы ![]() =
векторы кобазиса:
=
векторы кобазиса:
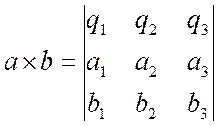
отсюда и из формул Т1 Þ ![]()
3.
Найти компоненты ![]() для ЦСК
для ЦСК
из формул Т3 Þ 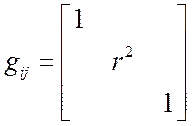 Объяснение,
почему много нулей
Объяснение,
почему много нулей
4.
Найти компоненты ![]() для ЦСК
для ЦСК
из формул Т3 Þ 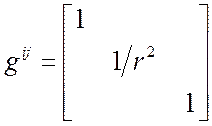
ДОМАШНЕЕ ЗАДАНИЕ: Найти компоненты ![]() для
ССК
для
ССК
из формул Т3 Þ 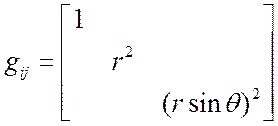
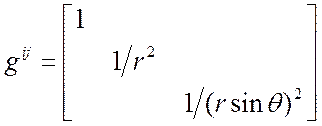
5.
Рассмотрим лишь 1-е уравнение;
остальные получаются жонглированием индексов:
![]() Þ
Þ ![]()
![]()
![]()
Заметим: ![]() Þ матрица
оператора
Þ матрица
оператора ![]() невырожденная в любом базисе
невырожденная в любом базисе
6.
![]() – базис в
– базис в ![]() ,
, ![]() , все
, все ![]() различны;
векторы
различны;
векторы ![]() Þ после подходящей нормировки
Þ после подходящей нормировки ![]() можно
принять за кобазис
можно
принять за кобазис
![]() Þ
Þ ![]()
7.
![]() ,
,
![]() , все
, все ![]() различны.
Найти матрицу
различны.
Найти матрицу ![]() в базисах
в базисах ![]()
Пусть ![]() Þ
Þ ![]() или в матричной записи
или в матричной записи 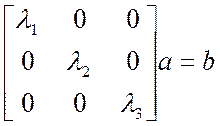
8.
Определить ![]() по аналогии с
по аналогии с ![]()
Т2 Þ 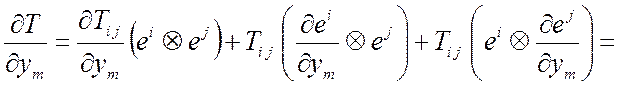
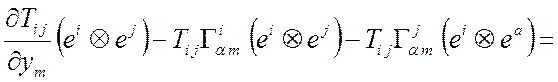
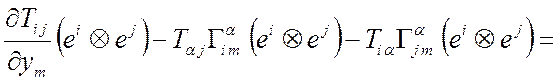
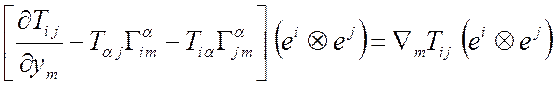
Þ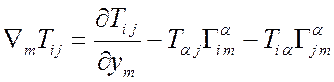
9.
Определить ![]() по аналогии с
по аналогии с ![]()
10.
Формула для вычисления ![]()
Д1 Þ 
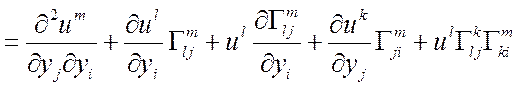
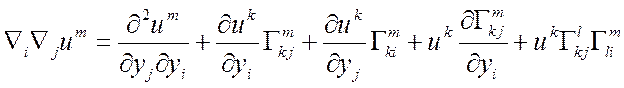
11.
Доказать: 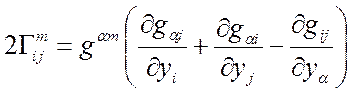
Т3, Д2 Þ 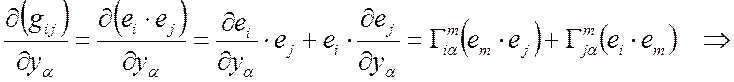
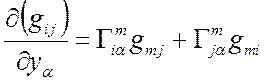 (1)
(1) 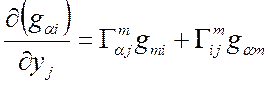 (2)
(2) 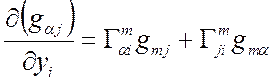 (3)
(3)
(2) + (3) – (1)Þ 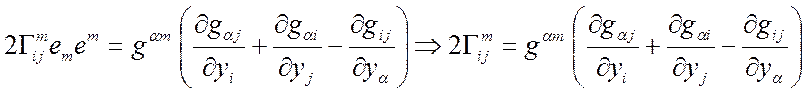
12.
Символы Кристоффеля для ЦСК, ССК
ЦСК: Д2, 1 Þ 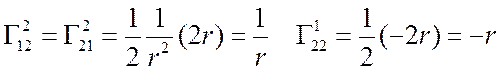 остальные
остальные ![]() = 0
= 0
ССК: Д2, 1, 8 Þ 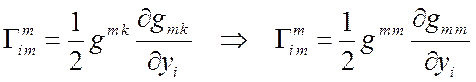 Þ
Þ
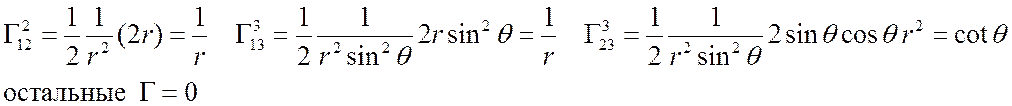
13.
Найти ![]() в ЦСК
в ЦСК
найдем ![]() затем поднимем индексы
затем поднимем индексы
ЦСК: Д3 Þ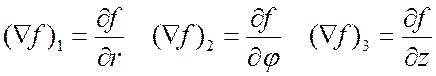
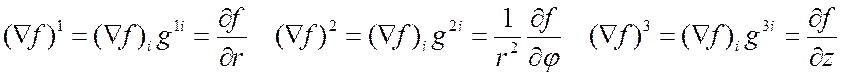
14.
Дивергенция векторного поля в
ПСК, ЦСК, ССК
ЦСК: 8 Þ выписать ![]() 9Þвычислить
9Þвычислить
![]()
Д5 Þ div F = 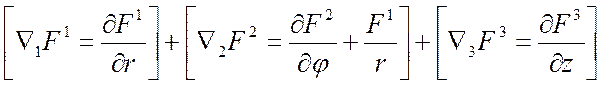
ПСК: из div F для ЦСК
удалить 3-е слагаемое
ССК: 8 Þ выписать ![]() 9 Þвычислить
9 Þвычислить
![]()
Д5 Þ div F = 
15.
Записать закон сохранения массы
в ПСК, ЦСК, ССК
Выражения для div F
из 10 вставить в Þ 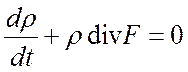
16.
Компонентная запись уравнения ![]() в ДСК, ПСК
в ДСК, ПСК
ДСК: Д6 Þ 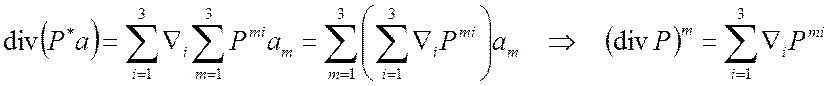
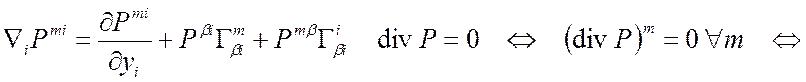
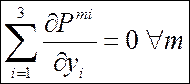
ЦСК: 8 Þ 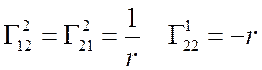 Þ
Þ
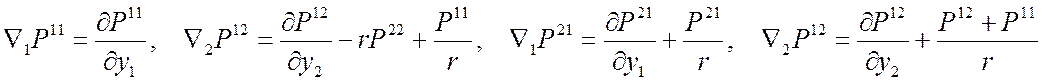
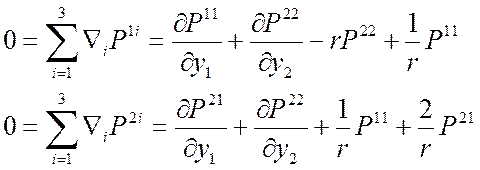
17.
Уравнение Лапласа в ДСК, ЦСК, ПСК, ССК
ДСК: ![]() ; все
; все ![]()
Д3 Þ градиент ск. функции = вектор 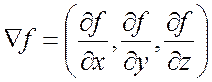
10 Þ дивергенция вектора div v =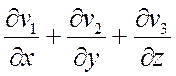
оператор Лапласа 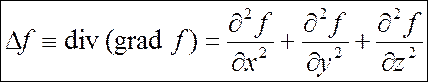
ЦСК: 1 Þ ![]() 8 Þ
8 Þ ![]()
9 Þ градиент функции 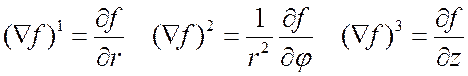
![]()
10 Þ дивергенция векторного поля div v = 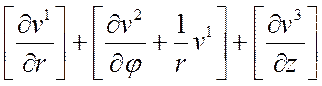
оператор Лапласа 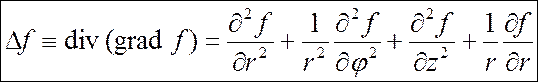
ССК: 1 Þ ![]() 8 Þ
8 Þ ![]()
9 Þ градиент функции 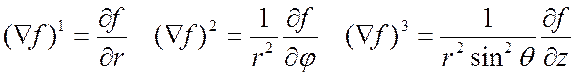
![]()
10 Þ дивергенция векторного поля div v = 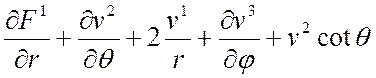
оператор Лапласа 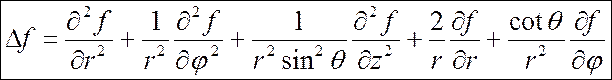
18.
Доказать: ![]()
f – скалярная функция Þ Ñf = вектор 
g – скалярная функция Þ Ñg = вектор 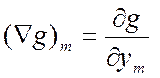
fg – скалярная функция Þ Ñ(fg) = вектор 
запишем и сравним компоненты левой-правой части
19.
f – скалярная, g –
вектор-функция. Доказать: ![]()
запишем и сравним компоненты левой-правой части
Д4 Þ ![]()
![]() см (14)
см (14) ![]() (1)
(1)
![]() (2)
(2) ![]() (3)
(3)
(1) = (2) + (3)
20.
F,
U – вектор-функции, U – постоянная. Доказать: ![]()
Д4 Þ ![]() ,
,
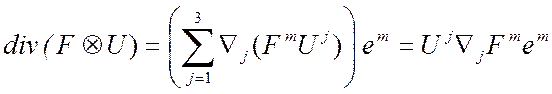 ,
, ![]() Þ
Þ ![]()
![]()
21.
F,
U – вектор-функции. Доказать: ![]()
Д4 Þ ![]() ,
,
![]() Þ первое слагаемое =
Þ первое слагаемое = ![]()
Аналогично второе слагаемое:
Д4 Þ ![]() ,
,
![]() Þ
Þ ![]()
Левая часть тождества:
![]()
![]()
22.
![]() –
скалярная, F – вектор-функция. Доказать:
–
скалярная, F – вектор-функция. Доказать: ![]()
![]()
ЗАКОНЫ СОХРАНЕНИЯ
|
|
Вспомогательные формулы
1. ![]() Вычислить
Вычислить
![]()
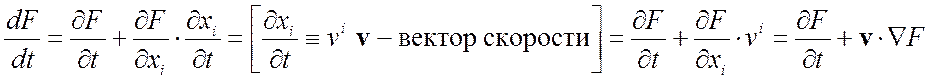
|
|
2. Вычислить div![]() (см
18)
(см
18)
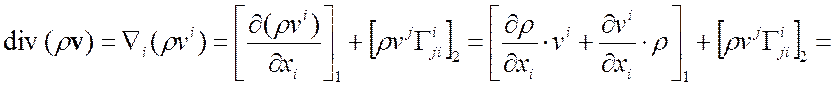

|
|
3. Как внести ![]() под знак
интеграла
под знак
интеграла ![]()
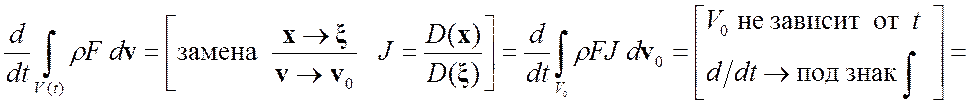
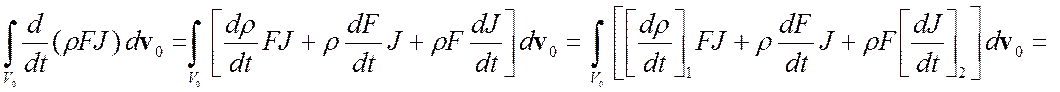
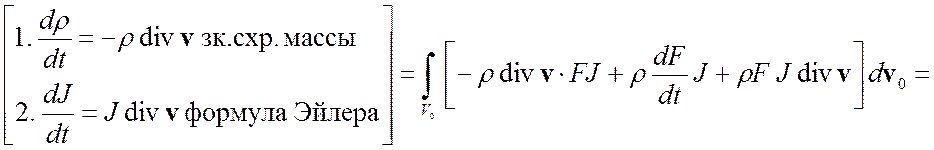

|
|
1.
Закон схр. массы Þ дивергентный вид
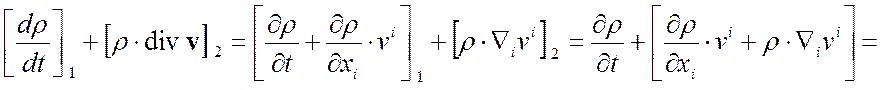

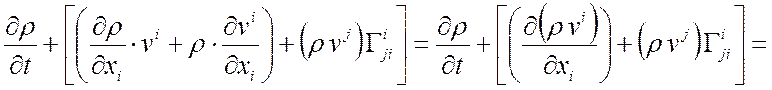

2.
Формула Эйлера 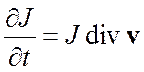
Используем формулы 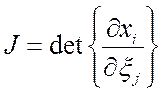 ;
; 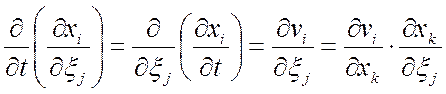
правила дифференцирования определителя и свойства определителя Þ
Þ 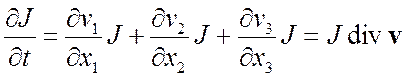
3.
Закон схр. импульса Þ дивергентный вид 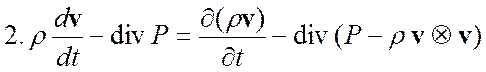
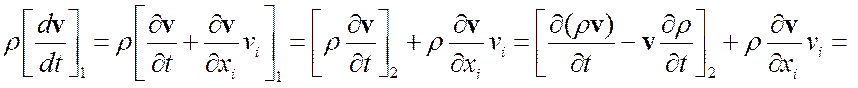
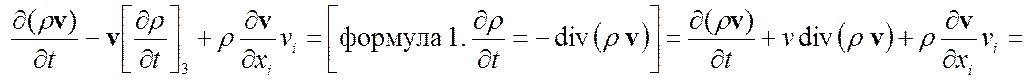
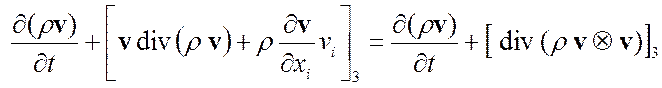 Þ формула 2.
Þ формула 2.
4.
Закон схр. энергии Þ дивергент вид 5. 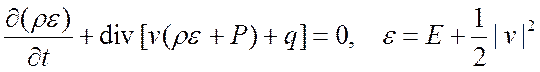
Дифф. форма закона 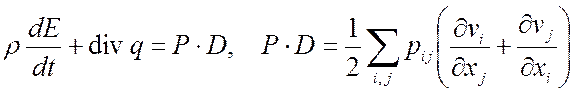 Þ
Þ
Интегр. форма закона 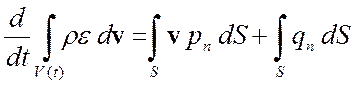
![]() – вектор потока тепла,
– вектор потока тепла, ![]() .
.
В левой части вносим ![]() пол интеграл,
пол интеграл,
правую часть преобразуем по формуле Гаусса-Остроградского:
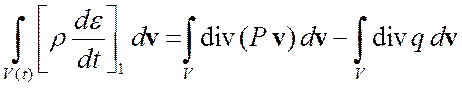 Þ
Þ 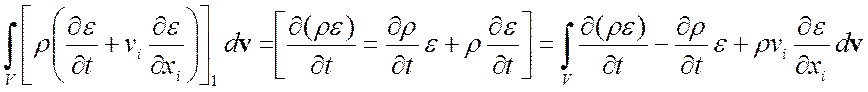
Из закона схр массы 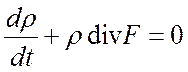 …
…
5.
Доказать: 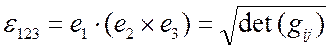
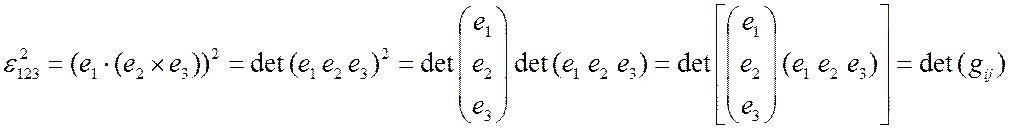
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.