Нахождение сингулярных чисел.
Составитель: Чеканников Сергей Петрович.
ММФ, 2курс, группа №0112.
Преподаватель: Махоткин О.А.
Поставленная задача: двумя способами найти сингулярные числа вещественной несимметрической матрицы.
Для матрицы A(n × n)
существует сингулярное разложение ![]() , где U и V — ортогональные матрицы. U составлена из собственных векторов матрицы C=AA’,
а V — из собственных векторов (по величине собственных
чисел) матрицы D=A’A (т.к.
AA’=
, где U и V — ортогональные матрицы. U составлена из собственных векторов матрицы C=AA’,
а V — из собственных векторов (по величине собственных
чисел) матрицы D=A’A (т.к.
AA’=![]() =U
=U![]() , где
, где ![]() —диагональная
матрица. Т.е. в точности является спектральным разложением, где U—матрица,
составленная из собственных векторов. Для V — аналогично) =>
—диагональная
матрица. Т.е. в точности является спектральным разложением, где U—матрица,
составленная из собственных векторов. Для V — аналогично) =>
![]() i =
i =![]() =
=![]() (т.к.
собственные значения AA’ и A’A равны
по предыдущему).
(т.к.
собственные значения AA’ и A’A равны
по предыдущему).
Если составить
матрицу H=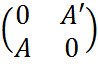 размерности (2n × 2n), то собственные значения матрицы H являются ±
размерности (2n × 2n), то собственные значения матрицы H являются ±![]() i . Также, если матрица A нормальная, т.е. AA’=A’A, то
i . Также, если матрица A нормальная, т.е. AA’=A’A, то
![]() i(A)=|
i(A)=|![]() i(A)|. Предлагается
исследовать 2 способа нахождения сингулярных чисел, и сравнения точности
нахождения и трудоемкости каждого метода.
i(A)|. Предлагается
исследовать 2 способа нахождения сингулярных чисел, и сравнения точности
нахождения и трудоемкости каждого метода.
1) Составляем матрицу M=AA’, находим ее собственные числа. С помощью функции sqrt из стандартной библиотеки math.h находим сингулярные числа.
2) Составляем матрицу H размерности 2n (которая будет симметричной), находим для нее собственные значения методом Якоби.
Блок-схема программы.
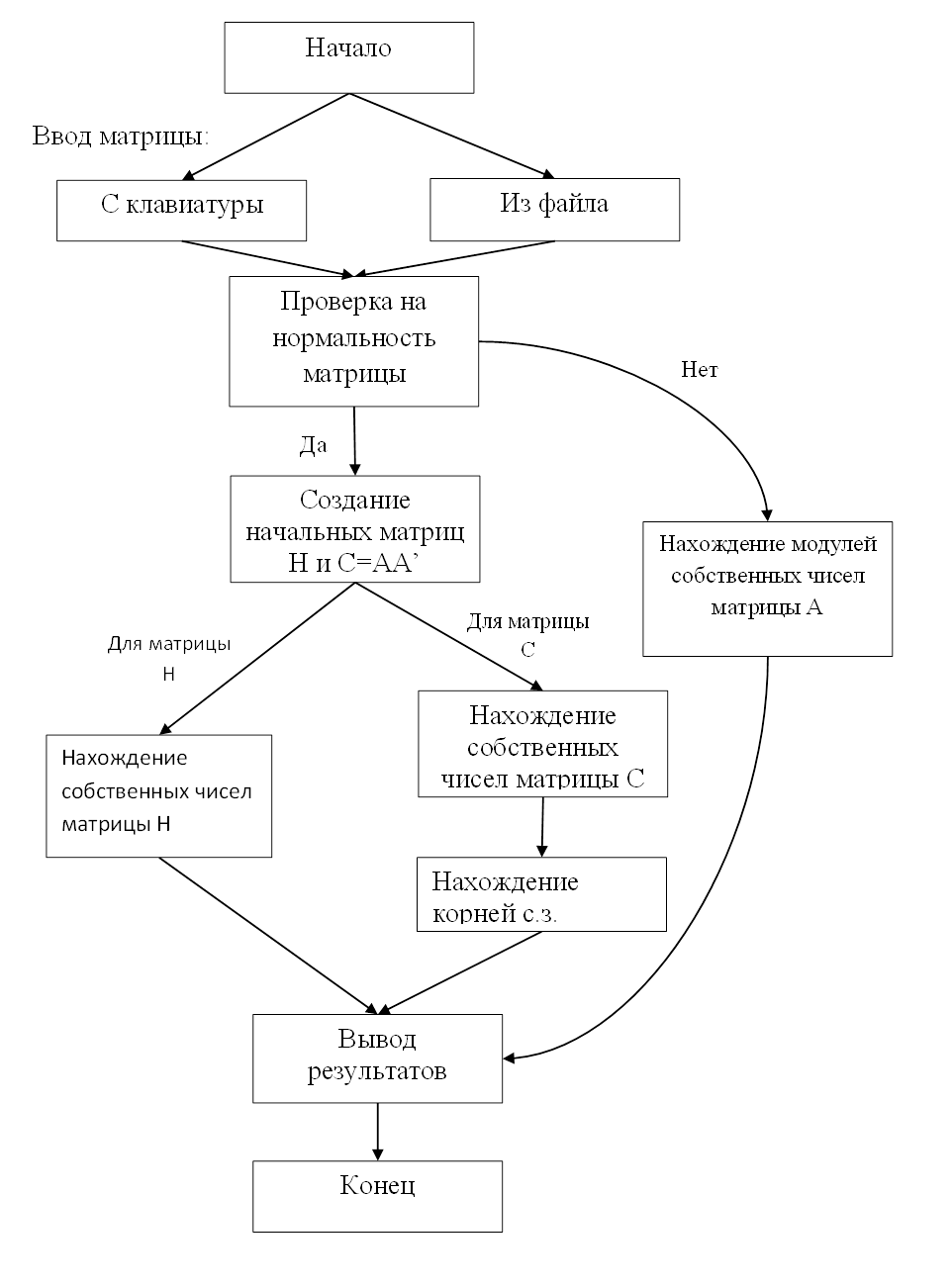
Введенные типы данных:
class vector — класс вектор.
class matrix — класс матриц.
Введенные функции:
Hconstr(matrix &A) — функция, создающая матрицу H.
Transp (matrix &A) — транспонирование матрицы A.
Float norm (matrix &A) —норма матрицы, выдает значение float (будем считать норму по максимальной сумме модулей элементов строк).
void jac (matrix &A) — преобразует матрицу A в диагональную, с собственными числами на диагоналях (матрица A получается с помощью применения к ней метода Якоби, с максимальным количеством итераций — 200, погрешность — 0).
Стандартная библиотека <ctime>. Из этой библиотеки используется тип clock_t и функция clock(), которая возвращает время, измеряемое процессором в тактах от начала выполнения программы, или −1, если оно не известно. Для получения времени в секундах надо поделить на константу CLOCKS_PER_SEC. Измеряет с точностью до миллисекунды. Создаем к примеру 2 переменных t1, t2 типа clock_t. Выполним в начале какого-то участка t1=clock(), и в конце t2=clock(). Найдем разность второго из первого и поделим на CLOCKS_PER_SEC (нужно учесть, что теперь переменная должна быть float). Получим время, которое понадобилось компьютеру, что бы выполнить этот участок программы.
Функция проверки на нормальность bool normmatrix (matrix &A). Для этого еще понадобиться функция вычисления нормы матрицы float normmatrix (matrix &A, int nom), которая по матрице выдает величину нормы (первую или вторую, зависит от nom). Если норма матрицы E=AA’-A’A меньше, чем какая-нибудь малая величина (можно задать как константу или считывать с клавиатуры), то матрицы считается нормальной.
Тестовый пример.
Матрица
A=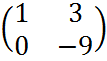 .
.
Матрица
C=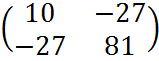 .
.
Матрица
H= 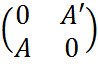 .
.
Сингулярные числа матрицы A по первому способу:
![]() 1(A) = 0.948152;
1(A) = 0.948152; ![]() 2(A) = 9.492155;
2(A) = 9.492155;
Сингулярные числа матрицы A по второму способу:
![]() 1(A) = 0.948151;
1(A) = 0.948151; ![]() 2(A) = 9.492150;
2(A) = 9.492150; ![]() 3(A) = - 0.948151;
3(A) = - 0.948151; ![]() 4(A) = -9.492152;
4(A) = -9.492152;
Реальные значения (wolframalpha.com) собственных значений по первому способу:
![]() 1(A) = 0.948151;
1(A) = 0.948151; ![]() 2(A) = 9.49215;
2(A) = 9.49215;
Реальные значения (wolframalpha.com) собственных значений по второму способу:
![]() 1(A) = 0.948151;
1(A) = 0.948151; ![]() 2(A) = 9.49216;
2(A) = 9.49216; ![]() 3(A) = - 0.948151;
3(A) = - 0.948151; ![]() 4(A) = -9.49216;
4(A) = -9.49216;
Численные эксперименты:
2)
3) Возьмем какую-нибудь несимметричную вещественную матрицу A. Для нее найдем время выполнения двух способов нахождения сингулярных чисел с помощью стандартной библиотеки <ctime>. Т.к. время выполнения компьютером такой небольшой программы будет очень маленьким, повторяем вычисления очень много раз, а потом, что бы найти время выполнения одного вычисления, делим на эту величину (к примеру, 200).
Возьмем произвольную матрицу (4×4).
1 -5 5 8
3 4.7 2.76 2
5 -9 8 -1.45
0 1 -0.004 0.1
Время выполнения по первому способу (повтор 200 раз):
t1=1.482;
Одного раза: t10=1.482/200= 0.00741;
Время выполнения по второму способу (повтор 200 раз):
t2=3.587;
Одного раза: t20=0.01793;
Т.е. трудоемкость второго выше в t2/t1≈2.41 раза.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.