Особенности решения СЛАУ большой размерности

УДК

О. А. Штейнбрехер

Новокузнецкий филиал-институт Кемеровского Государственного Университета

ОСОБЕННОСТИ РЕШЕНИЯ СЛАУ БОЛЬШОЙ РАЗМЕРНОСТИ

Аннотация

При решении краевых задач, например, задач расчета полей деформации и напряжений машинных конструкций, используются численное моделирование.[1, 2, 3] Для решения таких задач задач используются пакеты прикладных программ, такие как ANSYS, SolidWorks, T-FLEX.

Наиболее изучены задачи такого рода в линейной постановке, например, задача расчета полей деформации[2,3], на основе линейной зависимости. В случае линейной стационарной задачи метод конечных элементов[4, 5, 6] приводит к системе линейных алгебраических уравнений. В результате моделирования и дискретизации области расчета получается СЛАУ большой размерности.

Известны численные методы решения таких систем. Их можно разделить на прямые [6, 7] и итерационные[6, 7, 8]. Прямые методы обычно состоят из двух процедур – приведение матрицы системы к треугольному виду последовательным исключением или факторизацией, а вторая – обратная подстановка. К таким методам относятся метод Гаусса (рис. 1), разложение Холесского (рис. 2) и LDLт-факторизация.

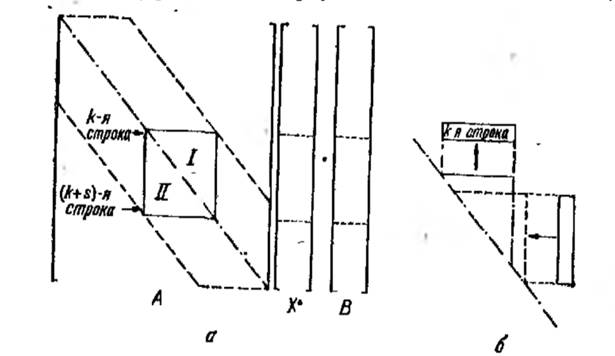
Рисунок 1 - Процедура исключения Гаусса: а) - рабочая область на k-ом шаге исключения; б) - изменение активной области при переходе от k-го к (k+1)-му шагу исключения

Особенностью прямых методов является то, что можно точно подсчитать количество арифметических действий, учитывая, что операции сложения выполняются намного быстрее, чем умножения и деления, обычно ограничиваются подсчетом последних, так для решения n-мерной СЛАУ методом Гаусса (без выбора главного элемента) требуется  умножений и делений. [7]

Разложение LDLт может быть выполнено весьма эффективно посредством вычисления элементов D и L по столбцам, эта процедура предпочтительнее простого метода исключения Гаусса, так как она значительно более быстрая. Разложение Холесского возможно только для симметричной положительно определенной матрицы коэффициентов. Оба алгоритма - LDLт-факторизация и разложение Холесского – требуют значительно меньше времени вычислений и, таким образом, дают более быстрое и дешевое решение по сравнению с простым методом Гаусса, хотя они не имеют больших преимуществ в отношении памяти. Процедура LDLт-факторизации содержит несколько меньше операций, чем алгоритм Холесского.

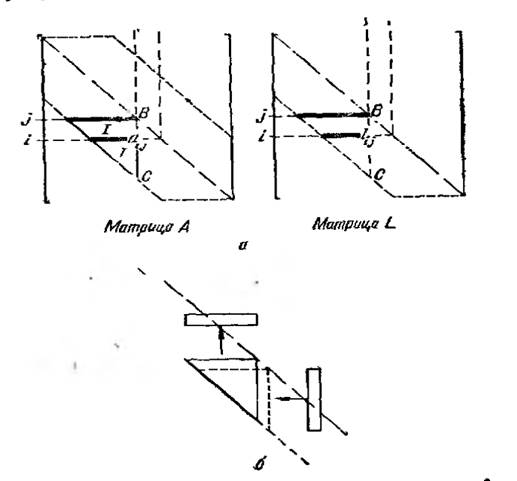
Рисунок 2 - Разложение Холесского: a) - рабочие области, б) - изменение активной области

В итерационных методах решение задачи требует повторяющегося применения алгоритма. Для начала итерационного процесса необходимо знать начальное приближение решения. При последующих итерациях получаются все более точные оценки решения, итерационный процесс заканчивается, если разность последовательных приближений становится меньше заданной величины. Итерационные методы по сравнению с прямыми имеют следующие преимущества: они а) могут эффективно справляться с разреженными матрицами, сохраняя и обрабатывая только ненулевые коэффициенты; б) требуют меньше оперативной памяти. [8]

Особенность итерационных методов градиентного класса заключается в том, что на решении уравнения достигается минимизацией квадратичного функционала. Градиентный метод (рис. 3 а) состоит из последовательных шагов от большого эллипсоида к меньшему, при этом точка, соответствующая решению, стремится по направлению к общему центру. Сходимость метода относительно медленная. Так же при попадании в особенности рельефа функционала (рис. 3 в, г), метод зацикливается. Метод сопряженных градиентов (рис. 3 б) действует лишь на положительно определенных и нормальных матрицах, условие сопряжения заключаются в том, что каждое последующее приближение ортогонально невязке.

Рисунок 3 - а) градиентный метод, б) метод сопряженных градиентов; виды рельефов: в) гребень, г) овраг

Существуют модификации итерационных методов, позволяющие увеличить скорость сходимости, например предобуславливатель. Скорость сходимости итерационных процессов зависит от числа обусловленности матрицы коэффициентов. Для её увеличения можно заменить исходную систему на равносильную, заменив матрицу коэффициентов A на матрицу , где матрица  - симметричная положительно определённая матрица – предобуславливатель.  Матрица предобуславливателя должна легко раскладываться на треугольные множители, а спектр предобуславливателя должен быть близок к спектру исходной матрицы. Предобуславливание ведет к увеличению скорости сходимости численных методов решения СЛАУ, но матрица предобуславливателя выбирается индивидуально для каждого метода.

Для решения СЛАУ большой размерности используются в основном итерационные методы.

Для уменьшения количества вычислительных операций и объема требуемой памяти используются, такие свойства матрицы коэффициентов, как симметрия, ленточность или разреженность. [5, 9] Можно выделить основные идеи технологий разреженных матриц: хранение только ненулевых элементов, оперирование только с ненулевыми элементами и сохранение разреженности. Конечно, не все алгоритмы для разряженных матриц достигают этих целей. Многие алгоритмы допускают определенную долю нулей, и алгоритм обрабатывает их, как если бы они не были нулями.

Для хранения ленточных матриц используются методы, хранящие в памяти лишь значения ленты матрицы. Если матрица симметрична, то достаточно хранить ее полуленту. Ширина ленты ленточной матрицы зависит от порядка, в каком расположены строки и столбцы. Поэтому перестановки строк и столбцов приводят к уменьшению ширины ленты. Малая ширина ленты означает снижение запросов к памяти, в вычислениях, связанных с матрицами, она обычно уменьшает и работу. В случае симметричной матрицы свойство симметрии будет сохранено, если для столбцов и строк используются одинаковые перестановки. [9]

Известно, что при решении конечноэлементной задачи, ширина ленты матричного уравнения системы зависит от способа нумерации узлов. Для простых конструкций или областей легко разместить узлы в некотором порядке, который минимизирует ширину ленты, но это становится почти невозможным в случае больших задач. [5]

Так как при решении задач методом конечных элементов матрицы коэффициентов получаются ленточными и разреженными, использование подобных методов позволяет уменьшить размерность задачи.

Лучшим вариантом является комбинация всех возможных средств: метода, способа хранения матриц и предобуславивателя. К таким можно отнести фронтальный метод[6, 8, 9], сформулированный для конечноэлементной задачи Айронсом в 1970г.[10]

В ленточных методах исходят из предположения, что до начала исключения в A суммирование завершено, и A полностью собрана. В фронтальном методе делается обратное предположение: исключение начинается прежде, чем будет законченно суммирование.