










Кто хочет сделать – ищет способ, кто не хочет – ищет причину
Конечномерная линейная задача (элементарная теория).
1. Основные понятия
Рассматривается система m – линейных уравнений с n – неизвестными:
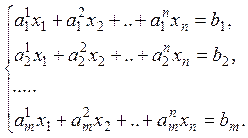
![]() Что
означает скобка? (и; и то , и другое).
Что
означает скобка? (и; и то , и другое).
Величины
![]() называются коэффициентами системы,
называются коэффициентами системы, ![]() – свободными членами,
– свободными членами, ![]() – неизвестные, которые надо
определить,
– неизвестные, которые надо
определить, ![]() – размерность задачи.
– размерность задачи.
![]() Совокупность
Совокупность ![]() чисел
чисел ![]() называется
решением системы, если при подстановке в систему на место неизвестных
все уравнения обращаются в тождество. Каждая такая совокупность называется частным
решением системы.
называется
решением системы, если при подстановке в систему на место неизвестных
все уравнения обращаются в тождество. Каждая такая совокупность называется частным
решением системы.
Пример: ![]() (1).
(1).
Решением являются пары чисел (1; 1), (2; 0), (0; 2) и т. д. Пара (1; 3) решением не является.//
В матричной форме система уравнений имеет вид:
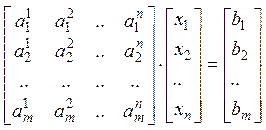 или
или ![]() ,
или
,
или ![]() – тензорная запись.
– тензорная запись.
![]() – основная матрица системы.
– основная матрица системы.
Задача: вычислить все ![]() для которых
для которых ![]()
![]() Система называется однородной,
если правая часть системы равна нулю (столбец
Система называется однородной,
если правая часть системы равна нулю (столбец ![]() –
нулевой), иначе неоднородной.
–
нулевой), иначе неоднородной.
(1) – неоднородная система.
![]() Система называется совместной,
если она имеет хотя бы одно решение (не менее одного), иначе несовместной.
Система называется совместной,
если она имеет хотя бы одно решение (не менее одного), иначе несовместной.
(1) – совместная система.
![]() Система называется определенной,
если имеет ! решение, неопределенной, если больше одного решения.
Система называется определенной,
если имеет ! решение, неопределенной, если больше одного решения.
(1) – неопределенная система.
Ограничимся
рассмотрением систем, когда ![]() .
.
2. Крамеровские системы линейных уравнений
Рассмотрим
систему из ![]() – уравнений с
– уравнений с ![]() – неизвестными:
– неизвестными:
В
матричной форме система имеет вид: 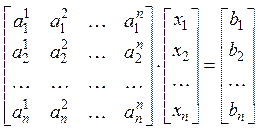
или
![]() .
.
Матрица
![]() называется основной матрицей системы
или главной матрицей.
называется основной матрицей системы
или главной матрицей.
Очевидно, что система не изменится, если
1) любое уравнение умножить на любое ненулевое число;
2) к любому уравнению прибавить любое другое,
3) переставить уравнения местами,
т. е. в результате получим равносильную систему.
Формулы Крамера
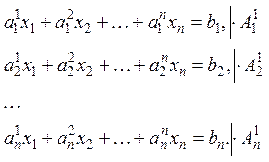 ,
,
сложим уравнения, получим:
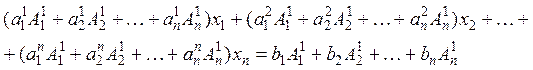
или
(вторая и т.д. скобки равны нулю по теореме) ![]() –
уравнение относительно
–
уравнение относительно ![]() , причем относительно
, причем относительно ![]() разрешима единственным образом.
разрешима единственным образом.
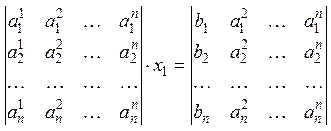 , тогда
, тогда 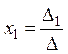 ,
где
,
где![]() .
.
Аналогично,
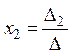 и т.д.
и т.д.
Т.
о. 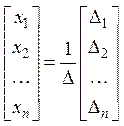 – формулы Крамера.
– формулы Крамера.
Решение
существует, если ![]() .
.
Вывод: если определитель системы отличен от нуля, то система имеет единственное решение, которое дается формулами Крамера.
Случай
![]() пока отложим.
пока отложим.
Пример: 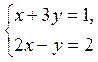 ,
, 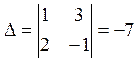 ,
, 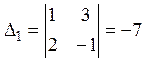 ,
,
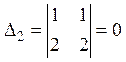 , значит
, значит ![]() .
.
3. Общее решение СЛАУ 2х2
1. Рассмотрим систему 2х2:
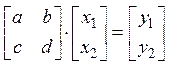
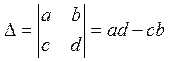 ,
, 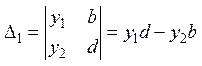 ,
,
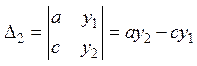 ,
,
следовательно
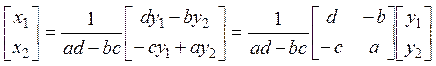
2. Обратная матрица к матрице 2х2
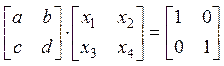 . Это уравнение эквивалентно двум
системам:
. Это уравнение эквивалентно двум
системам:
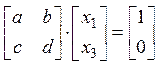 и
и 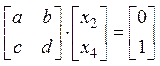 ,
тогда согласно примеру 1), получим
,
тогда согласно примеру 1), получим
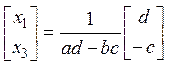 и
и 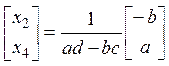 .
.
Таким
образом, 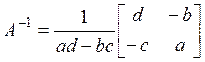
4. Расширенная матрица. Ранг
Рассмотрим
систему из ![]() – уравнений с
– уравнений с ![]() – неизвестными:
– неизвестными:
Если к основной матрице системы дописать столбец свободных членов, то получим расширенную матрицу линейной задачи:
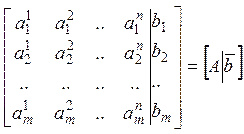 .
.
Матрица
![]() , в общем случае (
, в общем случае (![]() ), определителя не имеет, но из ее
элементов можно составить определители меньшего порядка.
), определителя не имеет, но из ее
элементов можно составить определители меньшего порядка.
![]() Минором
Минором ![]() -го порядка матрицы называется всякий
определитель, элементы которого лежат на пересечении любых
-го порядка матрицы называется всякий
определитель, элементы которого лежат на пересечении любых ![]() - строк и
- строк и ![]() -столбцов
матрицы.
-столбцов
матрицы.
Пример: 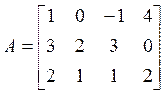 (2).
(2).
![]() :
: ![]()
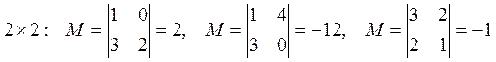
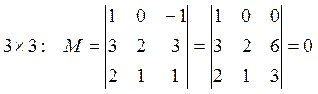
![]() Тогда ранг матрицы – это
наибольший порядок отличного от нуля минора. Обозначается
Тогда ранг матрицы – это
наибольший порядок отличного от нуля минора. Обозначается ![]() , сам минор называется базисным
(причем он определен неединственным образом), строки и столбцы матрицы, из
которых составлен базисный минор, называются базисными. Переменные, которые
соответствуют базисным столбцам, называются базисными, остальные небазисными
(свободными).
, сам минор называется базисным
(причем он определен неединственным образом), строки и столбцы матрицы, из
которых составлен базисный минор, называются базисными. Переменные, которые
соответствуют базисным столбцам, называются базисными, остальные небазисными
(свободными).
Пример:
![]() ,
,
![]() . Т. к. наибольший порядок
определителя, который можно составить из элементов матрицы, равен 3 (всего 3
строки в системе), то либо
. Т. к. наибольший порядок
определителя, который можно составить из элементов матрицы, равен 3 (всего 3
строки в системе), то либо ![]() , либо
, либо ![]() . Если среди миноров 3-го порядка
есть ненулевой, то
. Если среди миноров 3-го порядка
есть ненулевой, то ![]() , иначе
, иначе ![]() .
.
5. Леммы о ранге
![]() Столбец
Столбец ![]() является
линейной комбинацией столбцов
является
линейной комбинацией столбцов ![]() , если его можно
представить в виде
, если его можно
представить в виде ![]() , где
, где ![]() – коэффициенты, среди которых хотя
бы один отличен от нуля.
– коэффициенты, среди которых хотя
бы один отличен от нуля.
В
развернутом виде: 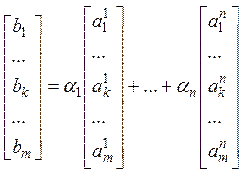 .
.
Лемма об усечении:
Ранг матрицы не изменится, если ее расширить нулевым столбцом или нулевой строкой. [Ранг не изменится, если убрать нулевой столбец или нулевую строку.]
Доказательство. Следует из определения ранга матрицы и свойства определителя(определитель, имеющий нулевую строку или столбец, равен нулю).
Лемма о ранге:
Расширение матрицы линейной комбинацией ее столбцов не меняет ее ранг.
Доказательство. Следует из определения ранга и распределительного свойства определителя.
Лемма:
Всякая небазисная строка есть линейная комбинация базисных строк.
Следствие.
Если линейная задача разрешима, то ![]()
Доказательство. Пусть ![]() – решение системы, тогда
– решение системы, тогда ![]() , а следовательно
, а следовательно ![]() является линейной комбинацией
является линейной комбинацией ![]() . Таким образом, по лемме о ранге
. Таким образом, по лемме о ранге ![]() .
.
![]() Если
Если ![]() ,
то
,
то ![]() :
:![]() ,
то это эквивалентно следствию. Если не
,
то это эквивалентно следствию. Если не ![]() ,
то не
,
то не ![]() :
:![]() –
контрапозиция.
–
контрапозиция.![]()
Если ![]() , то линейная
задача неразрешима.
, то линейная
задача неразрешима.
Следствие носит название теорема Кронекера - Капелли.
Пример. 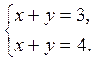 или в матричном виде
или в матричном виде 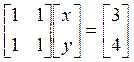 .
.
![]() , следовательно, система неразрешима
(несовместна).
, следовательно, система неразрешима
(несовместна).
6. Дефект линейной задачи.
![]() Дефект линейной задачи –
это разница между размерностью задачи и рангом основной матрицы:
Дефект линейной задачи –
это разница между размерностью задачи и рангом основной матрицы: ![]() . (Показывает количество небазисных
переменных).
. (Показывает количество небазисных
переменных).
Примеры:
(4.1) ![]() ,
, ![]() ,
т. е. нет небазисных переменных, значит решение единственное
,
т. е. нет небазисных переменных, значит решение единственное ![]() .
.
(4.2) ![]() ,
,
![]() , переменная
, переменная
![]() – базисная,
– базисная, ![]() –
свободная. Значит решений множество: (2; 1), (2; 0), …(2; с), т. е.
–
свободная. Значит решений множество: (2; 1), (2; 0), …(2; с), т. е. ![]() – любое. В матричном виде:
– любое. В матричном виде:
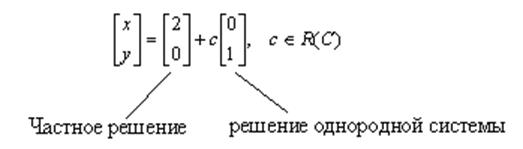
(4.3) ![]() .
.
![]() ,
переменная
,
переменная ![]() – базисная,
– базисная, ![]() –
свободные. Множество решений
–
свободные. Множество решений ![]() или в матричном
виде:
или в матричном
виде:
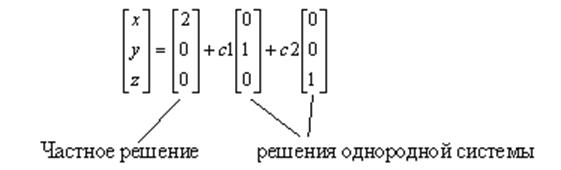
(4.4) 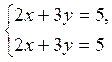
![]()
(4.5) 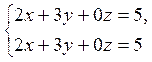
![]() .
.
Таким образом, общее решение системы есть сумма какого-нибудь частного решения и решений однородной системы:
![]()
![]() – частное
решение,
– частное
решение, ![]() – решение соответственной однородной системы.
– решение соответственной однородной системы.
![]() .
.
Любая
задача может рассматриваться как задача произвольной размерности, но не ниже
того числа ![]() , которое записано. Отсутствующие
переменные могут принимать произвольное значение независимо друг от друга.
(Примеры (4.2), (4.3)).
, которое записано. Отсутствующие
переменные могут принимать произвольное значение независимо друг от друга.
(Примеры (4.2), (4.3)).
7. Опорные решения
Рассмотрим
пример ![]() .
. ![]() , значит, решение
неединственное. Если
, значит, решение
неединственное. Если ![]() , то
, то ![]() . Т. к.
. Т. к. ![]() –
любое, то можно выбрать частное решение, положив
–
любое, то можно выбрать частное решение, положив ![]() :
: ![]() – опорное решение. В матричном виде:
– опорное решение. В матричном виде:
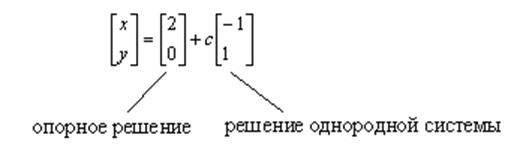
8. Линейная задача ранга 1
Т. е. из одного уравнения.
![]() .
. ![]() ,
размерность не меньше
,
размерность не меньше ![]() , дефект
, дефект ![]() не меньше
не меньше ![]() .
.
Схема решения: называется «аукни и откликнется».
«Аукаем»
ту переменную, коэффициент при которой не равен нулю. Пусть ![]() , полагаем
, полагаем ![]() тогда
тогда
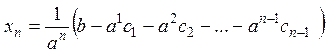 . Выпишем решение в матричном виде:
. Выпишем решение в матричном виде: 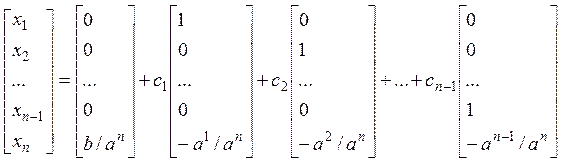 .
.
Дефект
![]() .
.
Особые линейные уравнения
1. ![]() – безразличное или тривиальное
уравнение. Является однородной системой. Множество решений
– безразличное или тривиальное
уравнение. Является однородной системой. Множество решений ![]() .
.
2. ![]() – несовместное уравнение. Является
неоднородной системой. Множество решений
– несовместное уравнение. Является
неоднородной системой. Множество решений ![]() .
.
9. Системы ранга 2
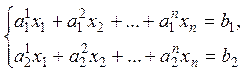
Если
![]() – множество решений первого
уравнения,
– множество решений первого
уравнения, ![]() – множество решений второго
уравнения, то множество решений системы есть их пересечение:
– множество решений второго
уравнения, то множество решений системы есть их пересечение: ![]() .
.
Если
![]() , то
, то ![]() .
Т. о. если система содержит тривиальное уравнение, то оно не влияет на решение
системы, а значит, его можно вычеркнуть.
.
Т. о. если система содержит тривиальное уравнение, то оно не влияет на решение
системы, а значит, его можно вычеркнуть.
Если
![]() , то
, то ![]() .
Т. о. если система содержит неразрешимое уравнение, то тогда система
несовместна.
.
Т. о. если система содержит неразрешимое уравнение, то тогда система
несовместна.
Рассмотрим
общий случай: ![]() .
.
Если
![]() , то
, то ![]() -тое
уравнение можно отбросить, т. к. оно не влияет на решение системы.
-тое
уравнение можно отбросить, т. к. оно не влияет на решение системы.
Если
![]() , то система неразрешима.
, то система неразрешима.
10. Элементарные преобразования и равносильные системы
Решение системы не изменится, если:
1.
в системе переставить местами
уравнения [в матричном виде: переставить местами строки в матрице ![]() ],
],
2.
перенумеровать неизвестные ![]() [перенумеровать столбцы в матрице
[перенумеровать столбцы в матрице ![]() ],
],
3.
умножить уравнение на ненулевое
число ![]() [умножить строку матрицы
[умножить строку матрицы ![]() на
на ![]() ],
],
4. к любому уравнению прибавить другое уравнение.
Элементарные преобразования не меняют ранг системы. Базисный минор элементарными преобразованиями можно «перегнать » в верхний левый угол. Тогда ранг будет равен количеству ненулевых строк полученной ступенчатой матрицы.
Пример: вернемся к примеру (2).
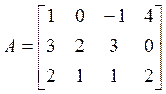 . Решим систему
. Решим систему ![]() , где
, где 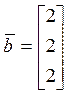 .
.
Выпишем расширенную матрицу системы и найдем ее ранг с помощью элементарных преобразований (приведем матрицу к ступенчатому виду):
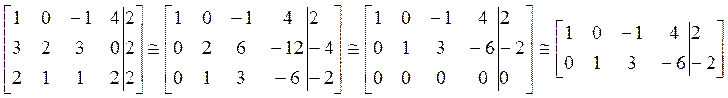
![]() , а значит система совместна.
, а значит система совместна. ![]() , следовательно решений множество.
, следовательно решений множество.
Пусть
![]() – базисные переменные (минор,
соответствующий этим переменным ненулевой), тогда
– базисные переменные (минор,
соответствующий этим переменным ненулевой), тогда ![]() –
свободные переменные. Найдем решение системы, для этого выразим базисные
переменные через небазисные (свободные) переменные:
–
свободные переменные. Найдем решение системы, для этого выразим базисные
переменные через небазисные (свободные) переменные:
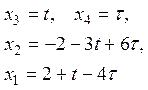
В
матричном виде:  ,
, ![]() .
(Рассказать про ФСР).
.
(Рассказать про ФСР).
Данный метод решения системы линейных уравнений носит название метод (схема) Гаусса.
2 этапа: 1. приведение системы к ступенчатому виду,
2. последовательное выражение базисных переменных через свободные, начиная с последнего уравнения.
11. Однородная линейная задача
![]() всегда разрешима
(
всегда разрешима
(![]() ).
).
![]() Рассмотрим
обыкновенное уравнение
Рассмотрим
обыкновенное уравнение
![]() . Если
. Если ![]() ,
то решение единственно
,
то решение единственно 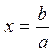 . Если
. Если ![]() , то все зависит от
, то все зависит от ![]() : если
: если ![]() ,
то
,
то ![]() – любой, если
– любой, если ![]() , то решений нет.
, то решений нет.![]()
То
же самое и здесь: если ![]() , то единственное решение
, то единственное решение ![]() . Если
. Если ![]() ,
то множество решений.
,
то множество решений.
Пример: 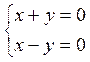
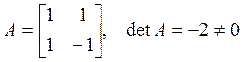 , в силу этого решение единственное –
нулевое:
, в силу этого решение единственное –
нулевое: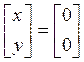 .
.
Или
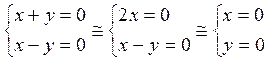 .
.
Пример: 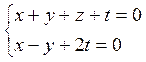
Найдем ранг матрицы с помощью элементарных преобразований и с помощью окаймляющих миноров:
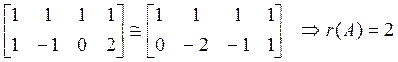 .
.
![]() ,
,
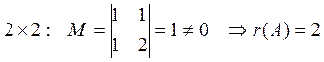 , значит, его можно взять в качестве
базисного. Тогда
, значит, его можно взять в качестве
базисного. Тогда ![]() – базисные,
– базисные, ![]() – свободные переменные. Выразим
базисные через свободные:
– свободные переменные. Выразим
базисные через свободные:
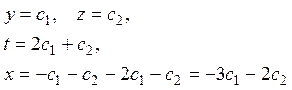 ,
,
тогда общее решение однородной системы будет выглядеть:
 .
.
Ясно,
что опорное решение является нулевым (![]() ).
).
Замечание. Линейная комбинация решений однородной задачи также является решением.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.