УДК 539
Т.В. Бурнышева
Новокузнецкий филиал-институт ГОУ ВПО «Кемеровский государственный университет»
ИССЛЕДОВАНИЕ СТАТИЧЕСКОГО ДЕФОРМИРОВАНИЯ ОРЕБРЕННОЙ ОБОЛОЧЕЧНОЙ КОНСТРУКЦИИ С ТЕХНОЛОГИЧЕСКИМИ ВЫРЕЗАМИ
В статье оценивается влияние выреза и окантовки на напряженно-деформированное состояние системы ребер и обшивки оребренной оболочечной конструкции. В результате численного эксперимента получены параметрические зависимости коэффициентов концентрации напряжений в оребренной оболочке от размеров выреза и модуля упругости окантовки. Определены поправочные коэффициенты к аналитическим оценкам фоновых напряжений в ребрах конструкции.
При проектировании оболочечных конструкций, применяемых в области машиностроения, конструктора выделяют ряд частных проблем, в том числе связанных с потерей устойчивости и снижением прочности за счет наличия вырезов конструктивного и технологического характера. Наличие сквозных технологических отверстий может вызывать местную потерю устойчивости и преждевременное разрушение конструкции. Поэтому необходимо анализировать как докритическое напряженно-деформированное состояние конструкции, так и устойчивость оболочки.
Известно, что методы решения задач статического деформирования и устойчивости элементов конструкций разделяются на точные и приближенные. Последние, в свою очередь, делятся на приближенные аналитические и численные методы [1].
В ранних работах В.В. Васильева, В.А. Бунакова оболочечная конструкция считалась континуальной, а решение непрерывно везде в её пределах. Такой подход к расчетам напряженного состояния конструкции требует в основном аналитических методов и меньше связаны с числовыми расчетами.
Наличие вырезов конструктивного и технологического назначения приводит к возникновению концентраций напряжений в их окрестности. Континуальная модель в этом случае резко завышает реальные напряжения в углах отверстий [2]. Избежать появления сингулярностей подобного типа позволяет модель, основанная на полном дискретном моделировании ребер. Использование такой модели дает реальную картину полей напряжений в окрестности вырезов.
Данный подход использовался В.В. Васильевым, В. А. Бунаковым, М. В. Никитиным, А. Б. Миткевичем, А.Ф. Разиным, А.П. Пономаревым в работах посвященных расчету напряженно-деформированного состояния конструкций с сетчатыми структурами. Однако НДС рассчитывалось либо для части конструкции, например, сетчатой панели без обшивки, вырезанной из цилиндрической оболочки [3], либо для сетчатой конструкции без технологических вырезов. Полное дискретное моделирование также применялось для рационального проектирования конкретных сетчатых конструкции и расчета концентрации напряжений в них: например, секционной крепи тоннелей в виде оболочечной конструкции сетчатой структуры [] (А.В. Суханов, В.Г Попов, Вл.О. Каледин). Результаты расчетов описывали НДС конкретной рассматриваемой конструкции при определенных нагрузках и не обобщались для всего класса сетчатых оболочек.
В работах [4, 5, 6] предложена общая методика расчета коэффициентов концентрации напряжений в ребрах и обшивке оболочек класса сетчатых оболочечных конструкций. Получены аппроксимирующие аналитические оценки напряжений и деформаций и поправочные коэффициенты к ним.
Для выбора рациональных размеров и формы отверстий было проведено исследование коэффициентов концентрации напряжений при варьировании размеров вырезов.
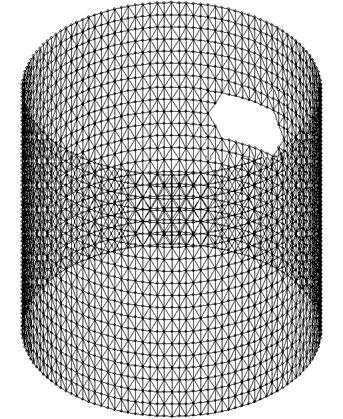
Численно решалась задача статического деформирования оребренной оболочки из полимерных композиционных материалов. На рисунке 1 приведена конструкция, которая представляла собой цилиндрическую оребренную оболочку, имеющую конструктивный вырез, расположенный в средней части. Оребрение состояло из пар спиральных и кольцевых ребер. Передняя кромка конструкции нагружалась сжимающей силой.
Математическая модель строилась на основе существующих теорий слоистых и подкрепленных оболочек. Дискретизация краевой задачи выполнялась методом конечных элементов. Схема разбиения обшивки на треугольные конечные элементы получалась естественным образом наложением оребрения. Для моделирования подкрепляющих элементов, представляющих собой балки сплошного прямоугольного сечения из полимерных композиционных материалов, использовалась сдвиговая модель балки Тимошенко [7]. Обшивка являлась достаточно тонкой, чтобы её можно было описывать в рамках гипотез Кирхгофа-Лява [8]. Задача решалась в физически и геометрически линейной постановке.
а) б)
Рисунок 1 – Цилиндрические оболочечные конструкции: а) без выреза; б) с вырезом
Для изучения влияния размера ширины выреза при фиксированной высоте на напряженно-деформированное состояние самой обшивки и ребер конструкции проводился численный эксперимент, при котором варьировалось число элементарных ромбических ячеек по ширине [9].
Расчетная
модель содержала 128 пар спиральных ребер. Нагрузка на одну пару спиральных
ребер бралась из условия 
, где 
- фоновые напряжения в конструкции
без выреза. Радиус оболочки R=831,982 мм. Спиральные и кольцевые ребра задавались
материалом со следующими физико-механическими характеристиками:
E1=E2=E3=3000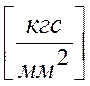
, G12=G13=G23=500, 
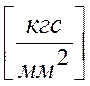=0,2.
Исходные физико-механические характеристики материала обшивки:
E1=408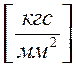
, E2=E3=6329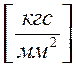, G12=G13=G23=367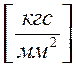, 1=0,72,
2=0,046, 3=0,046.
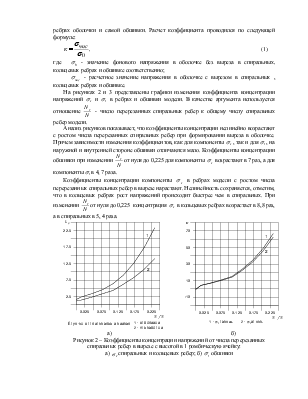
Высота выреза оставалась постоянной и была равна одной ромбической ячейки, ширина выреза в экспериментах изменялась по схеме: 1, 2, 4, 6, 8,…, 16 ромбических ячеек. Таким образом, максимальная ширина составляла ¼ от радиуса оболочки. В качестве отклика вычислялся коэффициент концентрации в кольцевых и спиральных ребрах оболочки и самой обшивки. Расчет коэффициента проводился по следующей формуле:
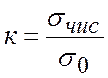, (1)
где - значение фонового напряжения в
оболочке без выреза в спиральных, кольцевых ребрах и обшивке соответственно;
- расчетное значение напряжения в
оболочке с вырезом в спиральных , кольцевых ребрах и обшивке.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.