Исследование статического деформирования оребренной оболочечной конструкции с технологическими вырезами, страница 3

а)

б)

Рисунок 10 – Напряжения в обшивке:

а – минимальные осевые напряжения, б – максимальные касательные напряжения;

1 – фоновые напряжения, 2 –напряжения на лицевой поверхности, 3 – напряжения на внутренней поверхности

При изменении  от нуля до 1,7 сжимающие окружные напряжения увеличиваются по абсолютной величине при изменении в 1,8-2 раза. Максимальные окружные напряжения при <0,8 уменьшаются, затем растут.

Рисунок 11 – Окружные напряжения в обшивке

а – минимальные, б – максимальные; 1 – фоновые напряжения, 2 –напряжения на лицевой поверхности, 3 – напряжения на внутренней поверхности

Полученные оценки показывают влияние некомпенсированного выреза на напряженно-деформированное состояние в оребренной оболочке, нагруженной осевым сжатием.

Достаточно часто сквозные вырезы в рассматриваемых оболочечных конструкциях усиливаются окантовками, что позволяет увеличить прочность конструкции. Однако, окантовки сами являются концентраторами напряжений, следовательно необходимо оценить их влияние на концентрацию напряжений конструкций.

Окантовка выреза выполняется заполнением пространства между ребрами композиционным материалом, армированным рубленным волокном либо тканью. Поэтому окантовка может иметь ширину, кратную размеру ячейки.

Оценим влияние модуля упругости материала окантовки (за счет степени наполнения) на концентрацию напряжений. Компенсирование выреза размером 4 ячейки по ширине и 2 ячейки по длине оболочки производилось одной окантовкой толщиной 30 мм, т.е. на всю высоту ячейки. Ширина окантовки в окружном направлении составляла две ячейки, в осевом – одну ячейку. При варьировании модулей упругости все компоненты матрицы упругости изменялись пропорционально.

На рисунках 12-14 изображено изменение максимальных растягивающих и сжимающих средних напряжений в ребрах (рисунок 12), обшивке (рисунок 13) и окантовке (рисунок 14) в зависимости от отношения 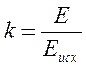, где E – модуль упругости материала в окружном направлении, берущийся для численного эксперимента, E_исх – исходный модуль упругости материала.

а)

б)

Рисунок 12 - Средние напряжения в ребрах при варьировании модуля упругости материала (E=kE_исх.): а – кольцевых; б – спиральных;

( ¾ сжимающие напряжения,  - - - - растягивающие напряжения)

На рисунке 12 отчетливо видно, что при увеличении модуля упругости средние напряжения в ребрах - как растягивающие, так и сжимающие - уменьшаются, причем, начиная с некоторого значения коэффициента k (примерно около 1,5) скорость этого уменьшения снижается.

Ту же зависимость можно проследить на рисунках 13, за исключением некоторого всплеска растягивающих напряжений  при k равном 0,5.

а)

б)

в)

Рисунок 13 – Напряжения в обшивке при варьировании модуля упругости материала (E=kE_исх): а) ; б) ; в) ;

( ¾ - сжимающие напряжения, - - - - -  - растягивающие напряжения)

а)

б)

в)

Рисунок 14 – Напряжения в окантовке при варьировании модуля упругости материала (E=kE_исх): а) ; б) ; в) ;

( ¾ - сжимающие напряжения, - - - - -  - растягивающие напряжения)

Напряжения в окантовке, как видно из рисунка 14, наоборот, стабильно возрастают при увеличении коэффициента k. Причем снижения скорости этого возрастания в отличие от предыдущих рисунков практически не наблюдается.

Проведенные исследования позволяют сделать следующие выводы.

Существенное влияние на изменение значений напряжений ребер обшивки оказывает варьирование модуля упругости материала окантовки и характерных размеров выреза.

Получены параметрические зависимости коэффициентов концентрации напряжений в оребренной оболочке от размеров выреза и модуля упругости окантовки.

Определены поправочные коэффициенты к аналитическим оценкам фоновых напряжений для некоторого практически важного диапазона структурных параметров сетки.

Эти результаты могут быть использованы для рационального конструктивного оформления зон вырезов

Литература

1. Вержбицкий В.М., Основы численных методов: Учебник для вузов/В.М. Вержбицкий. – М.: Высш. шк., 2002.

2. Андреев А.Н., Немировский Ю.В. Многослойные анизотропные оболочки и пластины: Изгиб, устойчивость, колебания. – Новосибирск: Наука, 2001. – 288 с.

3. Васильев В.В., Никитин М.В., Разин А.Ф. Исследование влияния формы ячейки на напряженное состояние композитной сетчатой конструкции при локальном нагружении // Вопросы оборонной техники. Сер. 15. Композиционные неметаллические материалы в машиностроении. – М.: НТЦ «Информтехника», 2008. – Вып. 1(138) – 2(139). – 90 с.

4. Каледин В.О., Аникина Ю.В., Бурнышева Т.В., Решетникова Е.В. Математическое моделирование статики сетчатой оболочки с учетом концентрации напряжений // Вестник ТГУ, 2006. - № 19. - С. 233-237.

5. Бурнышева Т.В., Каледин В.О., Решетникова Е.В. Дискретное моделирование напряжений в сетчатых оболочках // Краевые задачи и математическое моделирование [Текст]: сб. тр. 8-й Всеросийской науч. конф. - Новокузнецк: НФИ КемГУ, 2006. - В 2-х т. Т.2. - С. 16-19.

6. Каледин В.О., Миткевич А.Б., Бурнышева Т.В., Решетникова Е.В. Статическое деформирование композиционных сетчатых конструкций. Влияние обшивки на фоновые напряжения. Вопросы оборонной техники. Сер. 15. Копозиционные неметаллические материалы в машиностроении. – М.: ФГУП «НТЦ «Информатика», 2009. – Вып. 3(154) – 4(155). – 74 с.

7. Зенкевич О. Метод конечных элементов в технике. Пер.с англ. Под ред. Победри Б.Е. М.: Мир, 1975.

8. Разработка методики, алгоритмов и программ для расчета напряженно-деформированного состояния конструкций из композиционных материалов. Статика конструкций: Отчет о НИР; Руководитель В.О.Каледин; Г.р. №01850039154, Новокузнецк, 1985. – 102 с. –Деп. ВНТИЦ, инв. № 02860024610.

9. Спиридонов А.А. Планирование эксперимента при исследовании технологических процессов. М.: Машиностроение, 1981.—184 с., ил.