1. Термопара – очень маломощный источник эдс, поэтому нужно стремиться к уменьшению тока, отбираемого от нее в ходе измерения. Чем меньше термопара нагружена током, тем точнее сложившийся баланс электронов в месте горячего спая будет характеризовать разность температур. Среди возможных путей достижения этого можно назвать использование компенсационных методов измерения с нуль–гальванометром, усилителей с высоким входным сопротивлением (операционные усилители, полевые транзисторы во входных каскадах усиления и т.д.).
2. Так как величина термоэдс пропорциональна разности температур (t1 – t0) спаев, определить фактическое значение температуры горячего спая, расположенного непосредственно в зоне измерения, можно лишь в случае, если известна t0. Градуировка измерителя температуры была бы наиболее простой при t0 = 0 ˚C. Тогда выходная эдс термопары характеризовала бы фактическое значение температуры t горячего спая в градусах Цельсия.
Но для обеспечения стабильности t0 на объекте измерения часто не бывает условий. Поэтому, если принять, что горячий спай платино-платинородиевой термопары постоянно находится при одной и той же, неизменной, температуре t = 1400 ˚C, а t0 будет изменяться вместе с температурой окружающей среды, то при t0 = 30 ˚C термопара сформирует сигнал 13,974 мВ (что соответствовало бы t – t0 = 1370 ˚C), при t0 = -20 ˚C покажет 14.578 мВ (t – t0 = 1420 ˚C), хотя при правильно организованном измерении должна была бы показать 14,34 мВ. Поскольку такие погрешности измерения неприемлемы с точки зрения строгости поддержания технологического режима, уменьшение влияния температуры свободных концов на точность измерений является одной из главных задач.
3. Для уменьшения погрешности от изменения to холодный спай переносят в зону с относительно постоянной температурой (помещение операторской, например) путем удлинения выводов термопары подключением к ним специальных термоэлектродных проводов. Материал этих проводов желательно брать совпадающим с материалом электродов термопары, чтобы в месте соединения не возникали новые термоэдс. В случае термопар из благородных металлов можно использовать более дешевые материалы проводов (медь, константан, сплав ТП), лишь бы они развивали такую же термоэдс, что и электроды термопары. И только после этого можно минимизировать влияние температуры свободных спаев на точность результатов измерения. Как правило, это достигается термостатированием свободного спая и ( или ) корректированием изменения показаний термопары от вариации tо.
Компенсация погрешности показаний термопары от изменения tо
Как следует из статической характеристики платино–платинородиевой термопары (рис. 2), на основе которой будет строиться все дальнейшее рассмотрение, в диапазоне температур 1400 – 1600 ˚С величина ее выходной термоэдс изменяется примерно на Deтп = 1,2 мВ на каждые 100 ˚С изменения температуры. Это происходит независимо от того, увеличивается ли t при неизменной t0, или наоборот, уменьшается ли t0 при постоянной t. Главное в том, что термопара начинает давать заниженные показания при уменьшении разности t - t0.
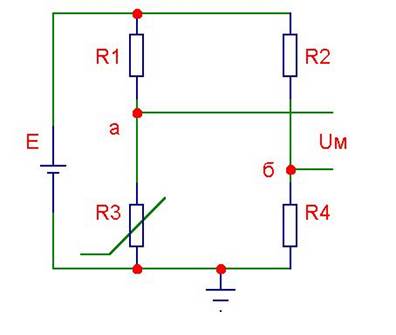
Поэтому компенсация погрешности должна строиться путем добавления к выходной термоэдс напряжения, зависящего от температуры t0, а по величине как можно больше приближенного к уходу показаний термопары. Такую поправку можно получить с диагонали неуравновешенного моста, в одно из плеч которого включен термозависимый элемент - терморезистор R3 (рис. 3).
Рис. 2
Выходное напряжение моста
E × (R2 × R3 – R1 × R4)
Uм =
,
(R1 + R3) × (R2 + R4)
получающееся по разности потенциалов jа - jб,
обращается в нуль при R1 × R4 = R2 × R3. Резисторы R1, R2 и
R4 выполнены из манганина для того, чтобы их величина
не зависела от температуры (температурный коэффициент сопротивления a у манганина близок к нулю).
Терморезистор R3 может быть выполнен из меди или никеля, поэтому его сопротивление
R3(t) = R3(0) (1 + a Dt) будет возрастать с повышением температуры
Рис. 3
холодного спая из-за того, что для меди a = 0,00426 1/град. При неизменном потенциале jб выходное напряжение моста будет создаваться приращением jа и будет равно
DUм = Е DR3 / (R1 + R3(0) + DR3).
Из уравнения для величины термоэдс видно, что она пропорциональна разности температур t – tо, поэтому нужно обеспечить условия, при которых DUм также имела бы пропорциональную зависимость от температуры, т.е. от ΔR3. Это означает, что ток через левую ветвь моста на рисунке 3 не должен зависеть от изменения R3, что равносильно выполнению неравенства R1 >> R3(0) + DR3, с учетом которого можно записать
DUм = Е DR3 / R1.
Кроме этого, для достижения независимости показаний датчика от температуры свободного спая термопары необходимо обеспечить равенство численных значений Dетп и DUм при одном и том же изменении температуры, т.е Dетп = DUм . После записи DR3 через ее составляющие получим основное уравнение для расчета параметров компенсирующего моста:
Δетп = E R3(0) α Δt / R1.
Если принять Е = 5 В, R3(0) = 25 Ом, а значение Δетп = 1,2 мВ выбрать исходя из диапазона изменения температуры Δt = 100 ˚С, то расчетные значения сопротивлений R1 = R2 получатся равными 44,375 кОм.
Полученные параметры моста близки по значениям к тем, которые обеспечивают достижение температурной компенсации. Их единственным недостатком является то, что номиналы резисторов R1 и R2 получились слишком большими. Если учесть, что R1 и R2 не должны зависеть от температуры и поэтому очень желательно наматывать их из манганиновой проволоки, то при таких номиналах это вряд ли целесообразно. Причина в том, что при расчете параметров моста начальные значения Δетп, Е и R3 намеренно выбирались как можно меньше, чтобы облегчить выполнение обязательного условия Δетп = ΔUм, а любое уменьшение номиналов R1 = R2 затрудняет его выполнение. Поэтому следует принимать другие решения для того, чтобы получать приемлемые значения сопротивлений R1, R2 без каких-либо ограничений на выбор остальных параметров компенсирующего моста.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.