Статистические аспекты имитационного моделирования (Раздел 8 учебного пособия "Моделирование систем"), страница 4

        К задачам планирования относятся задание начальных условий, процедура выборок, определение продолжительности и числа прогонов, определение пространства выводов о реальной системе, выбор средств имитационного моделирования, объем и вид документации о результатах моделирования.

        Задание начальных условий. Предлагаются три правила. 1. Запустить модель с состояния "пуст и свободен". Достоинство - простота. Недостаток - неопределенность начального состояния. 2. Запустить модель с модальных (с максимальной вероятностью) значений. Достоинство - начало соответствует наиболее вероятному состоянию системы. Недостаток - трудность определения модальных значений априори. 3. Запустить модель со средних значений. Достоинство - относительная простота определения средних значений. Недостаток - мала вероятность их.

        Процедура выборок. Выборки могут осуществляться через заданный интервал имитационного времени или при наступлении определенных событий. Важное значение имеет момент начала сбора статистических данных, так как начальные условия могут исказить результат имитации. Поэтому целесообразно за счет уменьшения количества собранной информации отсечь начальный участок прогона.

        Продолжительность и число прогонов. Использование нескольких продолжительных прогонов предпочтительней множества коротких. Продолжительность прогона можно контролировать по оценке исследуемого параметра: имитация прекращается, когда оценка дисперсии среднего выборочного становится меньше заданной величины.

        Число независимых повторных прогонов для достижения заданного доверительного интервала 1-  равно

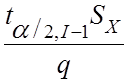                                         = ()²,

где  = - среднеквадратичное отклонение переменной ;  - половина доверительного интервала (точность оценки). Поскольку сами параметры ,   основаны на статистике, сначала делают любые  прогонов, находят  (по разбросу выборок ),  (по таблице -распределения Стьюдента для заданной доверительной вероятности и = -1), а затем уточняют  по   и  . Итерационные уточнения можно делать неоднократно.

        Определение пространства выводов. Пространство выводов касается диапазона изменения входных данных, чувствительности к уровням факторов, класса объектов, исследование которых можно проводить с данной имитационной моделью.

Однофакторный дисперсионный анализ. Суть однофакторного дисперсионного анализа сводится к определению влияния на результат моделирования одного выбранного фактора. Для доказательства независимости какого-либо параметра от выбранного фактора достаточно проверить гипотезу о равенстве средних значений выборок при различных значениях исследуемого фактора.

Корреляционный анализ. Позволяет делать статистические выводы о степени зависимости между переменными. Величина линейной зависимости между двумя переменными измеряется посредством коэффициента корреляции без учета влияния других переменных.

Регрессионный анализ.  На основе уравнений регрессии уточняет форму зависимости между переменными. Так, например, простая линейная регрессия для переменных ,  имеет вид:

                                                 =+ + ,

где =0, 1,…,;  - коэффициент регрессии;  - случайные ошибки испытаний, которые при модельной оценке  для заданного Πполагают равными нулю ( не известны при имитации). Цель регрессионного анализа - найти наилучшие в статистическом смысле оценки параметров , . Для этого при выбранных начальных параметрах ,  находят отклонение  между предполагаемым (по уравнению)  и его экспериментальным  значениями. Далее строят график зависимости =(). По виду графика делают заключение о степени адекватности модели и о направлении изменения исходных значений , .

Обобщенные оценки. Информационные системы, как правило, относятся к системам массового обслуживания. Анализ таких систем ведут на основе общих средних значений параметров. Рассмотрим примеры обобщенных оценок.

Простейшими системами являются системы с одним прибором, обрабатывающим поступающие запросы. Для них наибольший интерес представляет усредненное время ожидания и обслуживания при различных коэффициентах использования оборудования

                                  = .

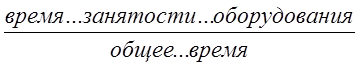Учитывая случайный характер поступления заявок, более точно коэффициент использования рассчитывают как

                                                  = ,

где  - среднее число поступивших запросов в единицу времени, - среднее время обслуживания одной заявки. Тогда среднее время пребывания одной заявки в системе

                                 =+,

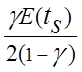
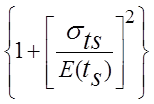где - среднеквадратичное отклонение времени обслуживания или его оценка по некоторому объему выборок.

        Среднее время нахождения в очереди одной заявки есть

                                 =.

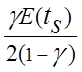
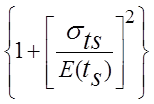        Среднее число заявок в очереди

                                 =+.

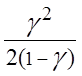
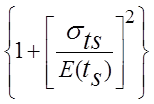        Среднее число заявок, ожидающих обслуживание,

                                 =.

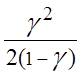
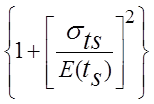Если в многоприборной последовательной системе одинаково загружены все  приборов (к этому необходимо стремиться), то для каждого прибора

                                          = /,

где ,  - параметры всей системы. В системах со многими направлениями, параллельными процессами и переключаемой структурой  обобщенная оценка параметров усложняется.